Кольцо в теории множеств — это непустая система R, замкнутая относительно пересечения и симметричной разности, т.е. операция пересечения или симметричной разности любых двух множеств обязательно приводит к множеству, содержащемуся в R. Это означает, что для любых элементов A, B из кольца, элементы A∩B и A∆B содержатся в кольце.
Круги Эйлера: что это и где применяются
Внештатный писатель, специализирующийся на статьях о питании, кулинарии, составлении бюджета и уходе за собой.
Дипломированный педагог-психолог с более чем 7-летним опытом работы в сфере совершенствования образования. Она является автором статей по вопросам образования и психологии.
Круги Эйлера — это простая диаграмма, с помощью которой можно показать взаимосвязь между общим и его частями. Это также помогает выявить логические цепочки между явлениями и понятиями.
Метод Эйлера использовался для упрощения задач во многих областях, от математики до управления. Он помогает находить ответы, выстраивая четкие логические цепочки.
Леонгард Эйлер (1707-1783) был швейцарским математиком, физиком, инженером и философом. Он долгое время (более 30 лет) работал в Академии наук в Санкт-Петербурге. Он внес большой вклад в становление российской науки.
Мы объясним, что такое круги Эйлера и как они используются в различных областях.
Виды кругов Эйлера
Эйлер выделял шесть типов отношений между понятиями, которые он выражал в соответствующих схемах.
- Равнозначные. Два одинаковых круга. Например, А.С.Пушкин = автор повести «Капитанская дочка».
- Пересекающиеся. Часть одного круга частично совпадает с частью другого (человек может быть одновременно и футболистом, и поэтом).
- Подчиненные. Один маленький круг внутри большого (корова относится к классу млекопитающих).
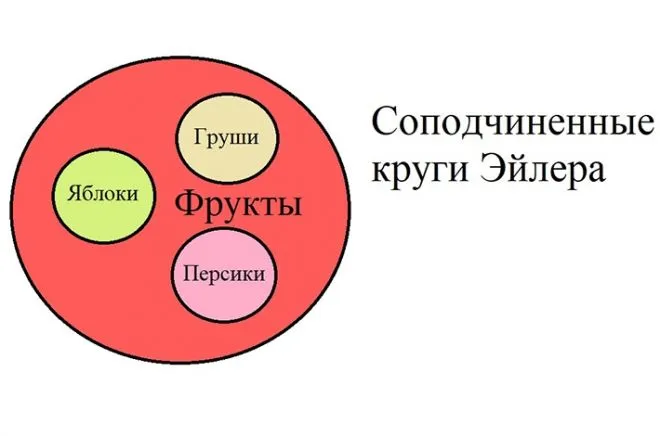
- Соподчиненные. Несколько одинаковых по размеру маленьких кругов внутри большого (яблоко, груша, персик – фрукты).
- Противоречащие. Разделенный пополам круг, каждая часть которого не имеет ничего общего с другой. Например, две конкурирующие между собой компании, производящие автомобили.
- Противоположные. Две части круга, между которыми есть свободное пространство. В отличие от предыдущей группы, между ними нет конфликта (холодное и горячее).
В сложной логической задаче иногда может быть несколько типов таких диаграмм одновременно.
Где применяются круги Эйлера
Круги Эйлера используются во многих упражнениях на мышление и логику. Сам ученый использовал этот метод для решения сложных математических задач, поскольку схематическое изображение простых схем может упростить мышление и сделать понятными возможные решения.
Сегодня круги Эйлера широко используются в его работах:
- математики;
- экономисты;
- маркетологи;
- менеджеры и др.
Основным преимуществом этого метода является его гибкость. Она подходит как для развития у детей навыков мышления, так и для решения сложных математических задач (и не только!).
Дополнение множества
Дополнением множества A является множество \(\overline A\), которое состоит из элементов, не входящих в A.
Однако все элементы, не принадлежащие A, не могут быть в \(\overline A.\) Предполагается, что все множества, участвующие в решении задачи, являются подмножествами общего универсального множества U:
Таким образом, дополнение \(\overline A\) представлено графически:

Объединение множеств
Объединение множеств A и B — это множество \(A\;\cup\;B\), состоящее из элементов, принадлежащих хотя бы одному из двух множеств.
Союз пишется следующим образом:
Таким образом, объединение множеств графически выглядит следующим образом:
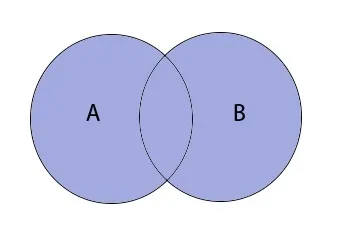
Пересечение множеств
Пересечением множеств A и B является множество \(A\;\cap\;B\), которое состоит из элементов, принадлежащих обоим множествам.
Пересечение множеств записывается следующим образом:
Это графически показывает пересечение множеств:
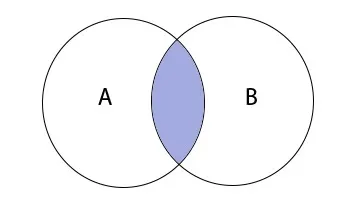
Типичный пример кругов Эйлера
Чтобы дать вам лучшее представление о том, как «работают» эйлеровы круги, предлагаем вам рассмотреть типичный пример. Чтобы привести типичный пример эйлеровой диаграммы, мы рекомендуем вам посмотреть на рисунок.
Часы (фиолетовые овалы) также являются частью игрушечного набора, но не связаны с набором производителя. С другой стороны, раненый автомобиль (желтый овал), хотя и является отдельным явлением, считается подмножеством раненой игрушки.
Многие задачи (в том числе познавательные), в которых участвуют круги совы, построены по аналогичной схеме. Рассмотрим одну из таких задач (которая, кстати, также была включена в демонстрационный тест ЕГЭ-2011 по информатике и ИКТ).
Условия задачи следующие: В таблице ниже показано, сколько страниц было найдено в Интернете по заданному поисковому запросу:
Пример решения задачи с помощью кругов Эйлера
Вопрос
| Количество найденных страниц (в тысячах) | Cruiser/Lincore |
| 7 000 | Kreuzer |
| 4 800 | Броненосец |
| 4 500 | Рабочий вопрос: Сколько страниц (в тысячах) выдаст поисковая система по запросу «крейсер и линкор»? Обратите внимание, что все запросы выполняются примерно в одно и то же время, поэтому общее количество страниц с искомыми словами остается неизменным с момента выполнения запросов. |
Для решения задачи: Для представления условий задачи используются эйлеровы круги, а цифры «1», «2» и «3» используются для обозначения результирующих отрезков:
Учитывая условия задачи, мы составляем уравнения:
Чтобы определить количество перехватов крейсеров и линкоров (на рисунке сегмент обозначен «2»), подставьте уравнение 2 в уравнение 1 и получите:
- Крейсер/линкор: 1+2+3 = 7 000;
- Крейсер: 1+2 = 4 800;
- Линкор: 2+3 = 4 500.
4 800 + 3 = 7 000, значит, 3 = 2 200 (так как 7 000-4 800 = 2 200).
Затем подставьте этот результат в уравнение 3 и получите:
2 + 2,200 = 4,500, а значит, 2 = 2,300 (так как 4,500-2,200 = 2,300).
Ответ: Для вопроса «Крейсеры и линкоры» найдено 2 300 страниц.
Этот пример наглядно показывает, что эйлеровы круги могут быть использованы для решения сложных задач достаточно быстро и просто.
Круги Эйлера — это очень полезная техника для решения задач и установления логических связей, а также интересный и веселый способ провести время и потренировать мозг. Итак, если вы хотите совместить работу с удовольствием и задействовать свой мозг, вы можете посетить курс «Нейробика», включающий различные упражнения, в том числе круг Эйлера, эффективность которого научно доказана и подтверждена многолетней практикой.
Резюме
Круги Эйлера и решение сложных логических задач с использованием свойств диаграмм можно продемонстрировать на примерах.
Советуем также прочитать:
- Сторителлинг
- Золотое сечение
- Евгеника: простыми словами о самом важном
- Монотипия: интересная и простая техника рисования
- Теорема Ферма и 380 лет на ее доказательство
- «Круги Сократа»: как диалектический метод используется в обучении
- Кубики Кооса
- Когнитивное развитие. Часть 1
- Математическое мышление
- Что такое нейрографика и чем она полезна?
- Хватит себе врать!
Решение задач, примеры
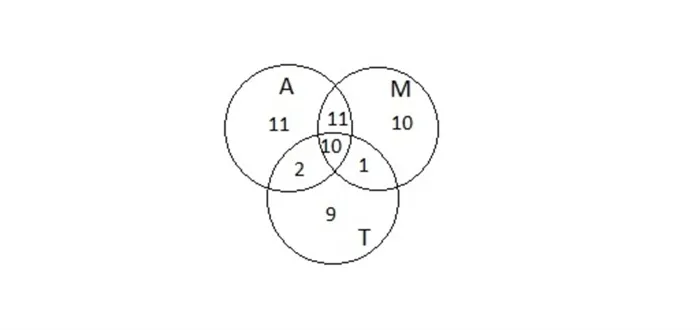
Задача 1. Представьте себе следующую ситуацию: 54 ученика шестого класса участвуют в занятиях по моделированию летательных аппаратов, музыке и танцам. Все они посещают как минимум один клуб. 32 студента занимаются музыкой, 22 — танцами и 34 — авиамоделированием. В музыкальных и танцевальных кружках занимаются 11 учеников, в музыкальных и авиамодельных кружках — 21 ученик, в кружках аэромоделирования — 12 учеников.
Теперь добавьте 22 студента-танцора. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22…. Опять же, некоторые студенты считают дважды. Из общего числа можно вычесть тех, кто занимается танцами и музыкой — 11 человек и 12 человек, которые одновременно занимаются авиамоделированием и танцевальными классами. Функция имеет следующий вид.
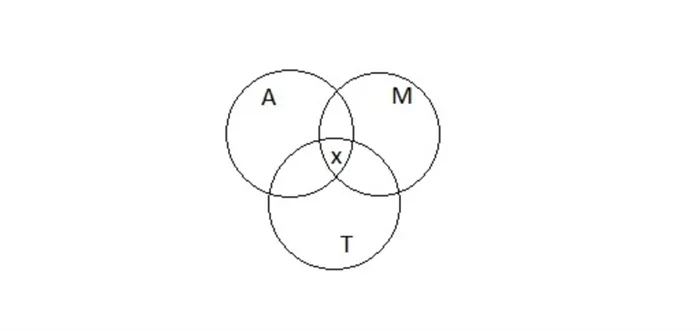
Однако студенты, посещающие все три цикла, вычитаются дважды. Их количество задается x и должно быть добавлено один раз к существующей формуле. Чтобы решить задачу, нужно определить x из уравнения (рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + x. Отсюда следует, что x = 10. Ответ: 10.
Рисунок 3
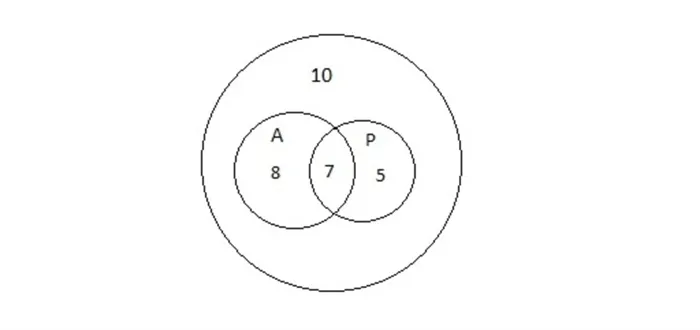
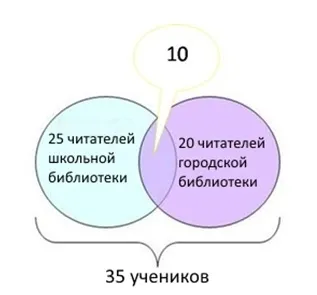
Задача 2. Тридцать учеников седьмого класса пришли в школьную библиотеку. 15 из них получили учебники по алгебре, 12 — по русскому языку, а 10 не получили ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Общие числа в диаграммах показаны на рисунке 4. В большом круге 30 учеников, а в двух маленьких кругах 30 — 10 = 20 учеников. Согласно заданию, 15 учеников получили учебники по алгебре, поэтому 20 — 15 = 5 учеников получили только учебники по русскому языку. Однако в условии указано, что 12 учеников получили учебники по русскому языку, поэтому 12 — 5 = 7 учеников получили учебники и по алгебре, и по русскому языку. Реакция.
Рисунок 4
Круги Эйлера часто используются для решения различных задач. Они используются для развития логического мышления у детей дошкольного возраста. Большая часть проблем студентов может быть решена с помощью диаграмм. Многие ученые также прибегают к этому методу в своих исследованиях, что повышает ясность решаемых проблем и способствует развитию мышления. Использование простых диаграмм может свести решение сложной задачи к символической логике и упростить рассуждения. Диаграммы можно использовать и в повседневной жизни, например, при поиске работы. Пересечение кругов «как можно лучше», «как можно приятнее» и «сколько можно заработать» может принести нужный результат.