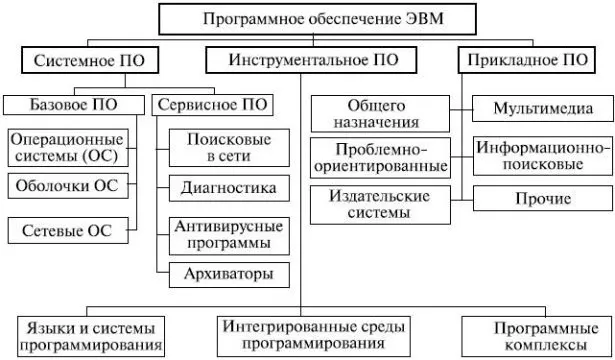
Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности могут быть выражены операциями отрицания, логического сложения и умножения, как показано в следующей таблице.
Логические утверждения могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, символы логических операций, логические константы (true и false) и круглые скобки. Логические выражения принимают значения true или false.
Правила построения логических выражений:
- любая логическая переменная или константа (истина и ложь) являются логическим выражением;
- если А —, то ¬А — тоже логическое выражение;
- если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А ~ В — тоже логические выражения.
Например, A ⊕ true v B v false является логическим выражением; A v ⊕ B v false не является логическим выражением.
Логическое выражение, которое принимает значение true для всех значений составляющих его переменных, называется тождественно-истинным выражением (тавтологией). Например: A против B против ¬A? (A ∧ ¬A) → B.
Логическое выражение, которое принимает значение false для всех значений составляющих его переменных, называется тождественно-ложным выражением (противоречием). Например, A ∧ ¬A? B ~ ¬В.
Логическое выражение, которое принимает как значение false, так и значение true при различных значениях составляющих его переменных, называется выполнимым выражением.
ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Сложные логические выражения, содержащие множество логических операций, имеют фиксированный порядок старшинства: сначала операция отрицания, затем операция логического умножения, затем операции логического сложения и исключающего сложения, и, наконец, операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения можно изменить с помощью скобок.
Приоритет логических операций в логических выражениях
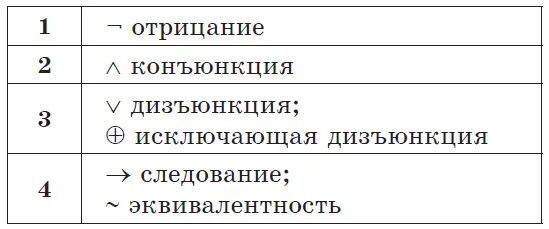
Пример 1Определите приоритет логических операций в выражении. Вычислите значение, если A = 1, B = 0, C = 1. ¬ A ∧ C v (A ⊕ B) ∧ B
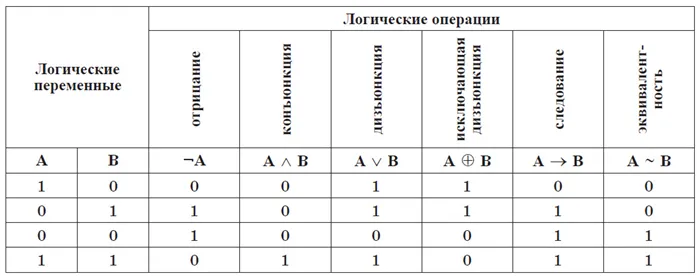
Решение. Значения в скобках рассчитываются в первую очередь. Затем операции выполняются в соответствии с их приоритетом: Операция отрицания имеет наивысший приоритет, за ней следует операция умножения, а затем операция сложения, как и в математике. Итак, порядок следующий:
Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках равно: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Сумма: 0. Ответ: логическое выражение ложно.
Пример 2К какому из приведенных слов верно следующее утверждение? (Вторая буква — гласная) ИЛИ (Первая буква — гласная) И НЕТ (Длина имени 5 букв или меньше)
1) Олег 2) Марианна 3) Светлана 4) Ольга.
- В соответствии с приоритетом выполнения операций сначала нужно вычислить результат операции отрицания: «Длина имени больше 5 букв». Такие имена — Марианна, Светлана .
- Затем необходимо рассчитать результат конъюнкции (связка И) второго и третьего высказываний. Конъюнкция истинна только тогда, когда истинны оба высказывания. Следовательно, нужно выбрать имена, в которых и первая буква гласная, и длина имени больше 5 букв — таких имен среди вариантов нет.
- Результат дизъюнкции (связка ИЛИ) истинен только тогда, когда истинно или одно, или второе, или одновременно оба простые высказывания. Первое простое высказывание истинно для имени Марианна, второе ложно для указанных имен. Таким образом, верный вариант ответа — 2.
Основные законы алгебры логики
Для сложных логических выражений с большим количеством переменных определение их истинностного значения путем построения таблиц истинности становится громоздким. В этих случаях мы используем методы
В преобразованиях эквивалентности сначала отмените отрицание выражений, а затем логические операции исключительной дизъюнкции, следования и эквивалентности. Затем используйте законы логической алгебры, чтобы уменьшить количество переменных в выражении.
Пример 4
Выберите выражение, которое эквивалентно (A ∧ B) v (Ā ∧ B).
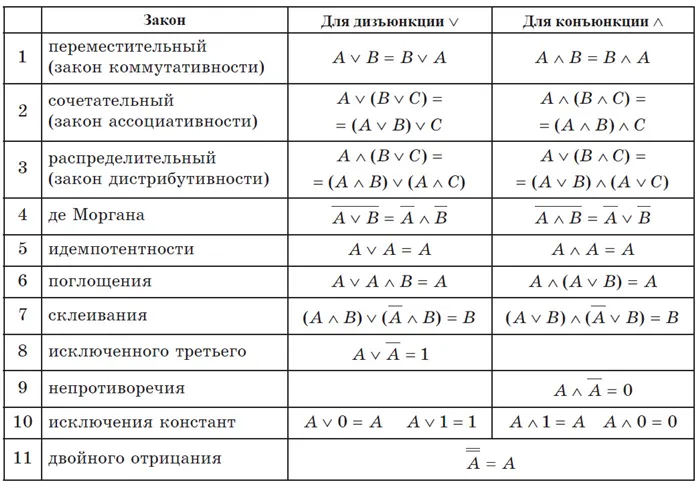
1) A 2) A ∧ B 3) Ā ∧ B 4) B
Решение. По закону конъюнкции (A ∧ B) v (Ā ∧ B) = B, поэтому исходное выражение эквивалентно B. Реакция.
Когда круглые скобки используются в логическом выражении, сначала выполняются операции, которые они содержат.Пример 5
1) 1 2) 2 3) 3 4) 4
Решение. В соответствии с порядком старшинства операций, сначала должны выполняться операции сравнения, затем отрицания и затем конъюнкции. Отрицанием утверждения M ≥ 10 является утверждение M
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
- Вычисление значений функций.
- Выполнение алгебраических операций (вначале возведение в степень, затем умножение и деление, после чего вычитание и сложение).
- Выполнение операций сравнения (в порядке записи).
- Выполнение логических операций (сначала операции отрицания, затем операции логического умножения, потом операции логического сложения, последними выполняются операции импликации и эквивалентности).
3. чтобы это выражение (конъюнкция) было истинным, оба неравенства должны быть выполнены (т.е. истинны). Следовательно, значение M должно быть больше 3, но меньше 10. Этому условию удовлетворяет только одно значение — число 4. Ответ.
Задачи, аналогичные предыдущему примеру, также можно решать с помощью таблиц истинности.Для какого из приведенных ниже значений числа М истинно следующее выражение? ¬М ≥ 10 ∧ M>3
Пример 6.
1) 1 2) 2 3) 3 4) 4<10. Получим выражение М<10 ∧ M>Решение. Давайте создадим таблицу истинности: Запишем все операции выражения в столбцы таблицы, а все предложенные значения M — в строки таблицы. Рассчитайте значения таблицы:
Как вычислить истинностное содержание логического выражения?
Термин «выражение» мы теперь знаем. Но что такое логическое выражение? Выражение — это уравнение высказываний, например, математическое уравнение чисел.Для какого из приведенных ниже значений числа М истинно следующее выражение? ¬М ≥ 10 ∧ M>3
Пример 6.
Истинность выражения определяется истинностью логических высказываний и логических операторов между ними.
Логические выражения и операторы
Например, о той же кошке я бы сказал: «Эта кошка вооружена и у нее голубые глаза». Это было бы откровенной ложью, потому что я использовал связку И, т.е. подразумевал, что оба утверждения верны, что не соответствует действительности. Но если бы я сказал: «Эта кошка вооружена или у нее голубые глаза», профсоюз ОР защитил бы меня от того, чтобы меня назвали лжецом. Я лишь указываю на истинность одного из двух утверждений.
Именно так работают логические операторы — в зависимости от них все выражение принимает значение true или false.
Основные логические операторы в алгебре логики:
Конъюнкция: логическое умножение или логическое И. В письменном виде он обозначается ∧. A ∧ B истинно только в том случае, если оба утверждения A и B истинны.
Его называют логическим умножением, потому что он работает аналогичным образом: Если хотя бы один из множителей равен 0, то все выражение равно 0.
Это называется логическим сложением из-за его сходства: Если мы добавим только 0 и 1, что мы и делаем, то единственное
В логических уравнениях высказывания используются в виде переменных, и основная проблема логической алгебры заключается в том, что точное истинностное содержание отдельных высказываний неизвестно. Назовем эту ситуацию «кот в мешке». Мы можем говорить о коте что угодно, но мы не узнаем, правда ли это, пока не заглянем в мешок. В таких случаях может помочь таблица истинности.
-
Таблица истинности — это таблица, которая дает истинностное содержание всего логического уравнения как функцию истинностного содержания каждой переменной.
Эта таблица содержит все возможные наборы переменных. Количество множеств N зависит от количества различных переменных i: N = 2 i .
Чтобы удобно записать наборы, пронумеруем их по порядку, начиная с 0, переведем их количество в двоичные числа (2cc) и запишем набор цифр.
Мы хотим создать таблицы истинности для известных логических операторов:
Заключение может быть выражено с помощью дизъюнкции: A ⇒ B = ¬A ∨ B
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквиваленция.
Поскольку мы знаем таблицы истинности отдельных операторов, давайте попробуем составить таблицу истинности для всего выражения.
Таблицы истинности
Например, для выражения: A ∧ (B ∨ C) ≡ B ⇒ ¬A.
Важно, чтобы порядок операций был правильным. Как всегда, сначала выполняется операция, указанная в скобках, а затем в порядке старшинства.
Порядок действий следующий:
Мы создаем таблицу, в которую сразу записываем все суммы 0 и 1 для переменных A и B и добавляем столбцы для каждого шага вычислений.
Чтобы было легче записывать предложения, пронумеруйте их по порядку, начиная с 0. Переведите их количество в 2 кубика и запишите сумму чисел. У нас есть 3 различные переменные, поэтому должно быть 8 предложений.
- инверсия берет только 1 переменную и сразу меняет ее значение:
- конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:
- дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:
- эквиваленция вернет 1, если переменные равны, и 0 в противном случае:
- импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:
| Последний столбец — это результат таблицы истинности. Отсюда видно, что общее исходное выражение равно 1, когда A = 1, B = 0 и C = 1, и что оно равно 0 во всех остальных случаях. |
Их не так уж мало: от самых простых и очевидных до самых сложных; от очень распространенных до очень редких.
Вам не обязательно знать их все наизусть — некоторые из них очень просты и напоминают правила математики начальной школы. Остальные стоит запомнить: если вы видите очень большое логическое уравнение, есть большая вероятность, что эти законы помогут его уменьшить.
Попробуем упростить исходное выражение ¬(¬A ∧ ¬B) ∨ B ∧ C:
¬(¬A ∧ ¬Γ) ∨ В ∧ Γ = ¬(¬A) ∨ ¬(¬Γ) ∨ В ∧ Γ
¬(A) ∨ ¬(C) ∨ В ∧ S = A ∨ В ∨ В ∧ S
A ∨ IN ∨ IN ∧ C = A ∨ IN
- Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.
- Третье действие — умножение значения А на результат первого действия:
- Четвертое — импликация значения В и результата второго действия:
- И последнее действие — эквиваленция результатов 3 и 4 действий:
В итоге нам удалось преобразовать уравнение с 3 переменными и несколькими отрицаниями в максимально простую нотацию, где осталось только 2 переменные:
Законы логики
¬(A ∧ ¬C) ∨ IN ∧ C = A ∨ IN
Таблица истинности — это табличное выражение результата логических операций для каждого отдельного набора значений переменных.
Такие таблицы позволяют убрать тривиальную информацию и сосредоточиться только на связях между исходными данными и происходящими процессами. Таким образом, можно убрать непонятную информацию и решить неспецифические проблемы.
- Первым можно увидеть закон де Моргана, где у нас идет отрицание целой скобки:
Для того чтобы использовать таблицы истинности, условие должно быть формализовано, т.е. необходимо избавиться от деталей задачи, указав следующее
- Здесь же появляются переменные А и В, к которым можно применить закон двойного отрицания :
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по следующим специальностям: Гитарист, плотник, егерь и стоматолог.
- Можно заметить закон поглощения — В складывается с умножением В на С:
Чтобы упростить логику, мы добавляем изображение зданий и присваиваем им номера:
Но дантист живет слева от егеря, а плотник — справа от егеря. Оказывается, что дом гитариста не может быть последним, а дом дантиста — позапрошлым. Таким образом, егерь живет в предпоследнем доме:
Между домами Андрея и Дмитрия есть дом, поэтому дом Андрея не может быть предпоследним, значит, число 4, что автоматически исключает проживание там Дмитрия и Владимира.
Табличный способ – этапы, особенности
Условие задачи занимает два предложения, а аргумент — две страницы.
Лучше не использовать этот подход, если ситуация сложная или имеется много данных.
Метод таблиц
Для решения задач с большим количеством данных (много предложений) лучше использовать таблицы или графики (диаграммы).
Чтобы создать таблицу истинности с логическими выражениями:
- Определить число логических значений/переменных (n) в примере.
- Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
- Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
- Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
- Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2 n + 1 (шапка).
- Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
- Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
- Сделать выводы на основании полученных результатов.
Для преобразования условия задачи в логические выражения и операции удобно использовать такую сводную таблицу истинности логических операций:
- с 2-мя переменными может быть только 4 набора логических переменных;
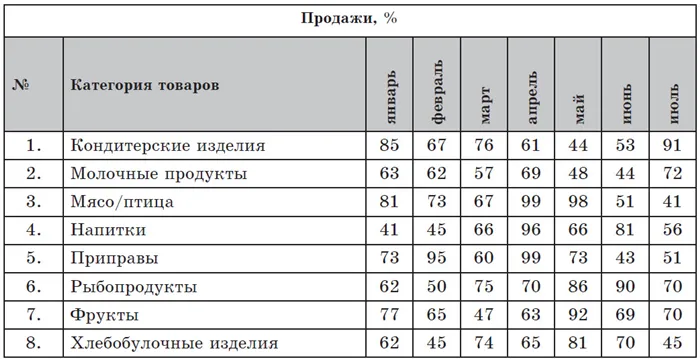
Возьмем тот же пример.
Мы обнаруживаем, что в первом доме может жить только гитарист, тогда мы проверяем записи и условия и получаем таких жителей:
- Указанные в скобках.
- Отрицание.
- Логическая конъюнкция чисел.
- Дизъюнкция.
- Строгая дизъюнкция.
- Импликация.
- Эквивалентность.
Обозначение логических операций:

Сравнение методов решения
Метод рассуждений
Метод более компактный, более описательный для некоторых проблем.
Несмотря на разнообразие проблем, многие условия повторяются, когда мы оставляем сухие формулы, не вдаваясь в имена, места и профессии. Поняв пример, вы сможете без труда решать подобные задачи. Рассмотрите некоторые странные проблемы, решив их логически.
Пример 2.
- дом плотника правее егеря;
- стоматолог проживает левее егеря;
- дом гитариста с самого краю;
- стоматолог живет рядом с гитаристом;
- Владимир не гитарист, и его дом не соседствует с гитаристом;
- дома Дмитрия и егеря соседние;
- здание, в котором прописан Андрей, правее стоматолога;
- между домами Андрея и Дмитрия один дом.
Известно, что если первый студент полетел в Англию на стажировку, то второй студент тоже полетел, но не верно, что если третий студент полетел в Англию, то второй студент тоже полетел.

Давайте разложим ситуацию на 3 простых утверждения и дадим им букву:

А — «Первый студент улетел в Англию»,

B — «Второй студент улетел в Англию»,
C — «Третий студент улетел в Англию».
Табличный метод
Запишем уточненные данные с помощью логических операций:
Пример 3.
- Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
- Записать условие задачи, как составное выражение из символов логических операций.
- Нарисовать таблицу истинности для полученных данных.
- Выбрать такой вариант, при котором полученные значения подходят под условие.
- Проверить соответствие выбранного варианта и условия задачи.
В 8 классе есть три класса (A, B, C), которые конкурируют за средний балл. Учителя сделали эти предположения в начале года:

В конце года выяснилось, что два прогноза были верными, а один — ошибочным.

Давайте посмотрим, какие классы получили лучшие оценки.


Разбейте проблему на элементарные утверждения:
Построение таблиц истинности для различных типов задач
A — «A получит лучшую оценку».
B — «B получит лучшую оценку».
С — «С получит высший балл».
Запишите логические операции
Известно, что в олимпиаде по химии участвовали четыре ученика 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девушек, если есть их высказывания о победителях, но в них верна только половина информации — первая или вторая половина предложения.
Маша Марина: «Саша занял второе место, а Света — первое.
Полина Света: «Нет, это неправда, Саша выиграл, а Галя вторая».
Таблицы истинности показывают, как может выглядеть выражение при различных значениях входящих в него переменных. Чтобы правильно их построить и выполнить вычисление логического выражения, необходимо следовать приведенному алгоритму. Таблицы строятся в следующем порядке:

Чтобы заполнить таблицы, необходимо упростить выражения, учитывая порядок операций. При этом обратите внимание, что если значение одного из аргументов функции в соответствующей строке таблицы равно нулю, то его необходимо записать в виде отрицания.
Предположим, вы хотите создать таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начните строительство с определения рядов. Если к этому примеру применить формулу 2n+1, то получится, что его номер: x = 22 + 1 = 5.
- Если А получит максимальный бал, то максимальный бал получат Ви С.
- А и С получат или не получат максимальный бал одновременно.
- Необходимым условием получения высшего бала С класса является получение высшего бала В классом.
Теперь определите количество столбцов. Для этого используйте формулу, учитывающую количество переменных и операций. Последнее можно рассчитать, просто сложив количество различных символов, используемых в введенной формуле. Однако правильнее сначала определить порядок операций, а затем подсчитать их. В зависимости от порядка выполнения операций они могут быть пронумерованы в следующем порядке:
Колонны выглядят следующим образом: Y = 2 + 5 = 7. Теперь нам нужно построить таблицу 7X5. В строке заголовка первого и второго столбцов напишите переменные, а затем операции с ними. Затем запишите на строках, соответствующих A и B, все, что может с ними произойти. Наконец, все, что осталось, это правильный расчет в последней колонке.
Используйте для этого законы. Значения в скобках должны быть логически умножены. Первый и второй ряды соответствуют операции произведения одного на один, что дает ответ один. Третий и четвертый — это ноль, умноженный на единицу, что в итоге дает ноль. Последний столбец является основным для данной логической функции. С его помощью можно найти значение логической функции для любой формы переменных A и B.
Это довольно простая задача, включающая всего две переменные. Однако в реальности, например, в программировании, их может быть гораздо больше. Решать такие проблемы методом перебора проблематично. Поэтому при решении сложных примеров мы сначала пытаемся упростить функцию.
Пример: дано выражение (x + y + z) * (x + y). На самом деле она написана в вполне нормальной связной форме. Но чтобы свести его к этой форме, нам нужен z во втором выражении. Чтобы добавить его, мы должны убедиться, что внутри скобок находится логическое дополнение. Поэтому добавление нуля не меняет результат. Сложение нуля на z выполняется путем умножения нуля на NOT z. В результате получается выражение (x + y + z) * (x + y + z + z), для которого легко составить таблицу по алгоритму.
В Интернете есть сервисы, которые автоматически создают таблицы истинности. Эти сайты предлагают свои услуги бесплатно и доступны даже людям с небольшим опытом. С их помощью можно найти таблицы для довольно сложных выражений, требующих тщательных вычислений. Онлайн-расчеты основаны на принципах логических законов, поэтому вам не придется беспокоиться о надежности результата. Кроме того, время, необходимое для расчета, минимально.
Чтобы воспользоваться компьютерными веб-сайтами, пользователь должен знать названия операций, иметь подключение к Интернету и установленный браузер, поддерживающий технологию Flash. Сервисы, предлагающие данный вид услуг, не требуют регистрации или предоставления персональных данных.

Среди различных порталов есть три особенно популярных калькулятора:
Эти сайты имеют интуитивно понятный интерфейс и, что очень полезно, на своих страницах они включают краткую теорию для таблиц истинности и даже примеры решений.
Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, в которой значения переменных и значение самой функции выражают истину. Например, они принимают значения true или false (истина или ложь, 1 или 0).
- последняя – гласная (Х1);
- или первая буква согласная (Х2)
- вторая – согласная (Х3).
Таблицы истинности используются для определения значения любого высказывания для всех возможных случаев истинностных значений высказываний, составляющих это высказывание. Количество всех существующих комбинаций в таблице определяется по формуле N=2*n-, где N — общее количество возможных комбинаций, а n — количество входных переменных. В цифровой механике и булевой алгебре таблицы истинности часто используются для описания работы логических схем.
Инверсия — Конвергенция — Связь — Ссылка — Эквивалентность — Линия Шеффера — Стрела Пирса.
Порядок построения (сборки) таблицы истинности:

Поэтому вы можете самостоятельно создать (построить) таблицу истинности.
Заполните поле ввода и нажмите OK. T означает истинный, F — ложный. Мы рекомендуем вам добавить эту страницу в закладки или сохранить ее в своей социальной сети.
Изучаем все » Математика в школе » Онлайн таблица истинности с примерами — Логика
Если вы нашли эту страницу полезной, пожалуйста, сохраните ее и поделитесь ссылкой со своими друзьями:
Алгоритм построения

- подсчитывают количество переменных n;
- вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
- определяют число логических операций;
- устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
- строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
- заполняют оставшиеся ячейки в таблице.
Пример задания
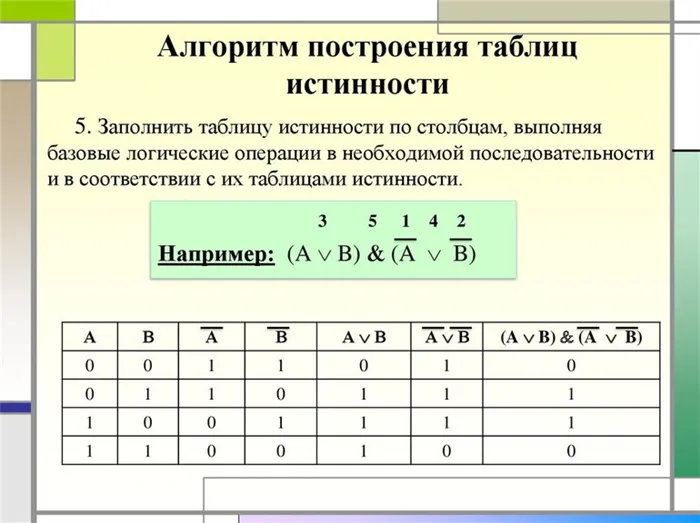
- Импликация в первой скобке.
- Инверсия во второй скобке переменной A.
- Отрицание во второй скобке неизвестной B.
- Сложение во втором члене.
- Конъюнкция.
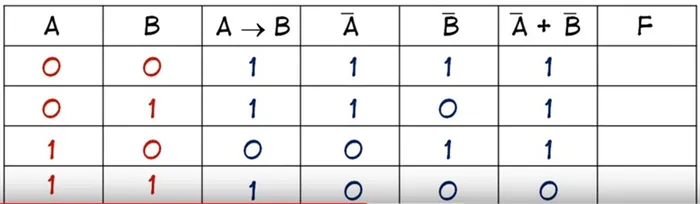
Вычисления онлайн
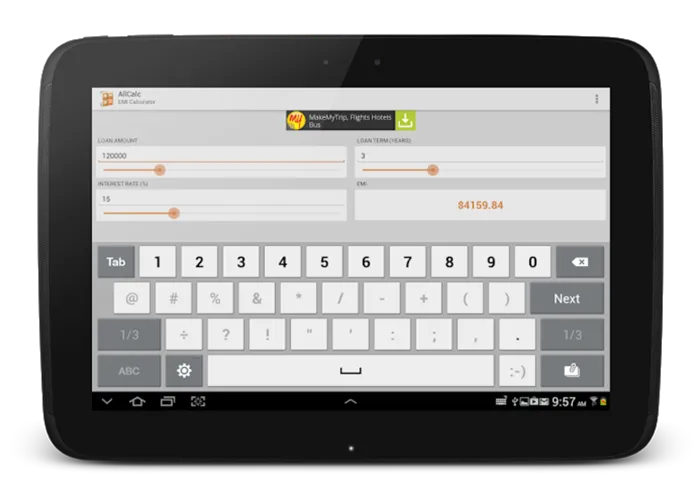
- Allcalc.
- Programforyou.
- Uchim.
Таблица истинности онлайн с примерами — логика
- Определить количество N используемых переменных в логическом выражении.
- Вычислить количество всевозможных наборов значений переменных M = 2 N, равное количеству строк в таблице.
- Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
- Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
- Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
- Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
- Заполнить окончательный столбец значений для функции F.
Составить таблицу истинности онлайн
- Множества или выражения большими буквами латинского алфавита: A, B, C, D.
- A’ — штрих — дополнения множеств
- && — конъюнкция («и»)
- || — дизъюнкция («или»)
- ! — отрицание (например, !A)
- \cap — пересечение множеств \cap
- \cup — объединение множеств (сложение) \cup
- A&!B — разность множеств A∖B=A-B
- A=>B — импликация «Если. то»
- A B — эквивалентность