Системы счисления в информатике: виды, примеры, характеристики. Что такое система счисления?

Они постепенно переходили от единиц к группам объектов по 3, 5 и 10 единиц. Постепенно эти группы были помечены определенными символами, что позволило уменьшить размер файла.

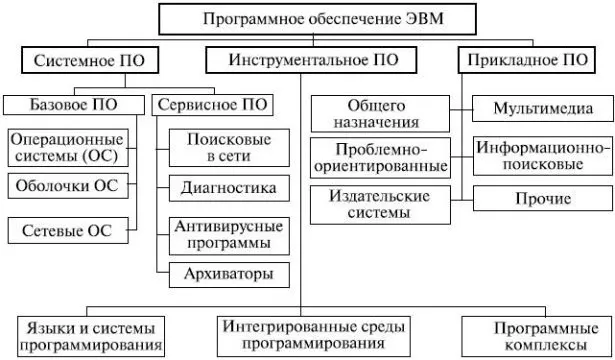
Что такое система счисления

Система нумерации — это символьный метод записи чисел, представление чисел с помощью символов.

Символы, используемые для записи числа, называются цифрами.

• даёт представления множества чисел (целых или вещественных)
• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
• отражает алгебраическую и арифметическую структуру чисел.

Разные народы в разное время использовали разные системы нумерации. Следы древних систем счисления можно найти и сегодня в культурах многих народов. Вавилоняне восходят к делению часа на 60 минут и угла на 360 градусов. В Древнем Риме существовала традиция записывать числа I, II, III и т.д. в латинской нотации. Для англосаксов — измерение десятками: в году 12 месяцев, в футе 12 дюймов, день делится на 2 периода по 12 часов.

По современным данным, развитые системы нумерации впервые появились в Древнем Египте. Для записи чисел египтяне использовали иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и акта сложения. Недостатками этой системы были невозможность записи больших чисел и ее неудобство.

В итоге десятичная система оказалась самой популярной системой счисления. Он состоит всего из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и позиция, в которой она находится. В числе 444 три одинаковые цифры обозначают количество единиц, десятков и сотен. В числе 400, с другой стороны, первая цифра обозначает количество сотен. Два 0 сами по себе не вносят никакого вклада в число, а нужны только для того, чтобы указать положение цифры 4.

Классификация систем счисления

Системы нумерации делятся на позиционные и непозиционные.

Позиционные системы счисления

Позиционные системы нумерации (ПНС) — это системы нумерации, в которых количественный эквивалент каждой цифры (ее вес) зависит от ее положения в числе.

В ходе длительной эволюции человечество выработало позиционный принцип записи чисел, который заключается в том, что каждая цифра, содержащаяся в числовой записи, занимает определенную позицию, называемую разрядом. Цифры считаются справа налево. Каждая цифра всегда больше предыдущей на определенный коэффициент. Это отношение называется основанием системы счисления (в неположительных системах счисления термины «разряд» и «основание» не существуют).

Пример: номер 237 состоит из 3 цифр. Ясно, что одна цифра 7 больше цифры 2. Однако, как часть числа, двойка находится на месте сотен, а семерка — на месте единиц, так что количественное представление двойки остается двести или двести семь.

1. шестидесятиричная (Древний Вавилон) — первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин);
2. двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 — «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава — всего 12;

Алфавит системы счисления — это набор различных цифр, используемых в позиционной системе счисления для записи чисел. Например: Десятичная система: Двоичная система: Октавная система: Шестнадцатеричная система:

• в позиционных системах счисления устранены все недостатки непозиционных:
• в них можно записать любое число (как натуральное, таки действительное);
• запись чисел компактна и удобна;
• благодаря поразрядной организации записи чисел с ними легко проводить математические операции.

Непозиционные системы счисления

Количество цифр в алфавите соответствует основанию системы счисления. Основание системы счисления — это количество цифр или знаков, используемых для представления числа в данной системе счисления.

Основой системы наименований является последовательность чисел, в которой каждая цифра имеет количественное значение или «вес». E.G: Основы некоторых систем ценности места. Десятичные: 10 0, 10 1, 10 2, 10 3, 10 4 ,…, 10 n ,…. Двоичные: 2 0, 2 1, 2 1, 2 2 2, 2 2 2, 2 2 2, 2 3, 2 4 ,…, 2 n ,…. Октава: 8 0, 8 1, 8 2, 8 3, 8 4 ,…, 8 n ,…. Пример. Десятичное число 4718.63, двоичное число 1001.1, восьмеричное число 7764.1, шестнадцатеричное число 3AF.

I	V	X	L	С	D	М
1	5	10	50	100	500	1000

Положение цифры в числе называется разрядной единицей: Цифры увеличиваются справа налево, от младшей к старшей цифре, начиная с нуля.

Русские не знали цифр, они заменяли их буквами с соответствующими значениями. Цифры обозначались специальным символом — титло — горизонтальной волнистой линией. Например, буква A соответствовала цифре 1, B — цифре 2, D — цифре 3. Десятки были представлены отдельными буквами: I — 10, К — 20, К — 30 и так далее, и сотни: С — 200, Х — 600.

• если большая цифра стоит перед меньшей, они складываются, например: VI – 6 (5+1);
• если меньшая цифра стоит перед большей, то из большей вычитается меньшая, причем в этом случае меньшая цифра уже повторяться не может, например: XL — 40 (50-10), XXL – нельзя;
• цифры М, С, Х, I могут повторяться в записи числа не более трех раз подряд;
• цифры D, L, V могут использоваться в записи числа только по одному разу.

Алфавит и основание системы счисления

526 написано следующим образом.

Египтяне использовали различные символы для обозначения чисел: для единиц они использовали вертикальные линии, для десятков — похожую букву «L», для сотен — похожую букву «e» и т.д. Например, 345 записывалось следующим образом.

Вавилоняне использовали SS с числом 60 в основании. Таким образом, наше время составляет 60 минут, а минута — 60 секунд. Эта СС отличалась сложным методом символизации цифр.

Вавилонская и древнерусская системы считаются самыми древними из известных систем счисления.

Самая древняя система записи чисел

Были разработаны новые СС для выполнения расчетов в электронном виде. Они сложны и непонятны для людей, но эффективны для машин.

Существует два типа систем нумерации: Позиционные системы и унифицированные системы.

Выберите правильный: Символы, используемые для записи чисел в системе нумерации, называются:

Позиционная система нумерации — это наиболее распространенный тип системы нумерации, в которой положение цифры влияет на значение числа, а окружающие ее значения — нет. Каждый символ представляет собой одну единицу соответствующего разряда. Например, десятичный SS позиционируется. Если цифра пять находится в последней позиции, она обозначает единицы, вторая — десятки, четвертая — тысячи. Символ один и тот же, но значение разное

Найдите правило перевода целых десятичных чисел в двоичные из формулы (1′).

Разделить а

Определение и виды систем счисления

• Возможность записать все числа в нужном диапазоне.
• Естественность представления – любой из комбинаций соответствует только одно значение.
• Обеспечение простоты восприятия и выполнения операций над числами.
• Возможность точного (без или с минимальными погрешностями) перевода значений в другие СС.

— 2 n-1 + a

— 2 n-2 + … + a

1. Алфавитом.
2. Основанием.
3. Числовым рядом.

Позиционная система счисления: что это

— 2 0 умножить на 2. Коэффициент равен a

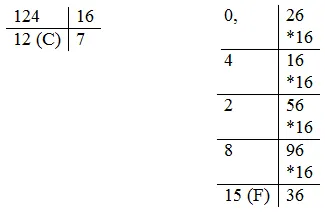
— 2 n-2 + … + a

• Простота запоминания и изображения чисел.
• Удобство совершения математических и логических операций.
• Миниатюрная запись огромных значений.

а остаток равен

• Обладает минимальными таблицами умножения, сложения.
• Представит любое число посредством двух состояний: единица и ноль.
• Помехоустойчивая по причине всего пары состояний.
• Проста в выполнении арифметических операций.

Полученный коэффициент снова делится на 2, а остаток является a

1.1.2. Двоичная система счисления

Если продолжить этот процесс деления, то на n-ом шаге мы получим набор цифр

которые являются частью двоичного представления исходного числа и соответствуют остатку от последовательного деления на 2.

• 10011₂Итак, чтобы перевести десятичное целое число в двоичную систему счисления, нужно разделить данное число и получившиеся целые части последовательно на 2, пока не получится часть, равная нулю. Исходное число в двоичной нотации составляется путем записи получающихся остатков один за другим, начиная с последнего.₁₀.

Пример 4. Переведем десятичное число 11 в двоичную систему счисления. Описанная выше последовательность операций (алгоритм перевода) может быть представлена следующим образом:

Если мы запишем остаток от деления в направлении, указанном стрелкой, то получим: 11

= 1011_n-1Пример 5. Если десятичное число достаточно велико, то более подходящей является следующая нотация вышеприведенного алгоритма:_n-2= 101101011₀Восьмеричная система счисления — это позиционная система счисления, основанная на числе 8. Цифры восьмеричной системы счисления — 0, 1, 2, 3, 4, 5, 6, 7._n-1= 101101011₁Например: 1063.₀.

= 1 — 8 3 + 0 — 8 2 + 6 — 8 1 + 3 — 8 0 = 563₁.

Таким образом, чтобы перевести восьмеричное целое число в десятичную систему счисления, мы должны перейти к расширенной системе счисления и вычислить значение полученного выражения.

Чтобы перевести целое десятичное число в восьмеричную систему счисления, необходимо разделить это число и полученные целые части на 8 последовательно, пока целая часть не будет равна нулю. Исходное число в новой нотации дополняется путем последовательной записи получившихся остатков, начиная с последнего.

Пример 6. Переведем десятичное число 103 в восьмеричную систему счисления.

База: q = 16.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, C, C, D, E, F.₁₀Здесь только десять из шестнадцати цифр имеют условное обозначение 0,…, 9. Первые пять букв латинского алфавита обычно используются для записи цифр с десятичными эквивалентами 10, 11, 12, 13, 14, 15.₂.

Поэтому обозначение 3AF

• 363₁₀означает:₂

1.1.3. Восьмеричная система счисления

= 3 — 16 2 + 10 — 16 1 + 15 — 16 0 = 768 + 160 + 15 = 943

Пример 7. Переведем десятичное число 154 в шестнадцатеричную систему счисления.

Система, на которой основаны компьютеры, была изобретена гениальным немецким ученым Г.В. Лейбницем (до 19 века!). Он изобрел и описал СС, в которой все расчеты производятся с использованием d₈Объяснение. Расширенная форма символики 579: 5*10 2 +7*10 1 +9*10 0 = 579₁₀.

Источник

Обычно мы используем сокращенную нотацию чисел, т.е. без деления и умножения оснований.

А чтобы было проще, мы используем готовую таблицу коэффициентов, равных 2.

1.1.4. Шестнадцатеричная система счисления

Сначала запишите числа, равные двум, начиная с наибольшего:

Затем нужно вычесть из числа максимальную степень двойки и поставить 1, если в основании есть единица, или 0, если ее нет. Перевод 579

Обратный путь еще проще. Посчитайте количество цифр — это мощность от 2 д о-1. И так далее. И проще использовать одну и ту же таблицу:

Если оно на 1 больше, то число начинается и заканчивается 1, а внутри — сплошной 0.₁₆Основание этой системы — 8, а числа в восьмеричной системе — 0-7. Эта система счисления является тематической и целочисленной. Он используется в областях, связанных с цифровыми технологиями, особенно с программным обеспечением Linux (права доступа, исполнение).

• 3AF₁₆Это 16-ричная система целых чисел (шестнадцатеричные цифры 0-9 и буквы от A до F), используемая в приложениях низкоуровневого компьютерного программирования и документирования, поскольку она представляет собой 8-битный байт и для записи требуется 2 шестнадцатеричные цифры.₁₀.

В стандарте Unicode используется 4 или более 16 символов SS.

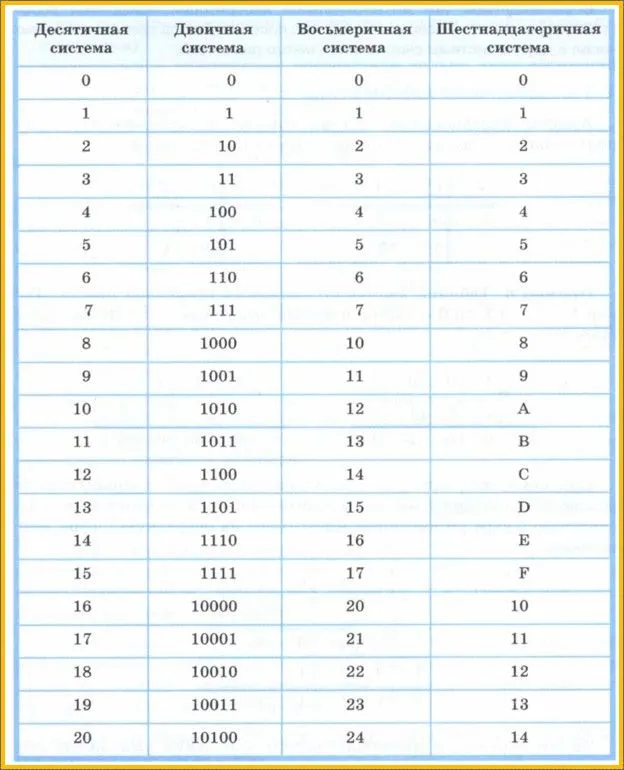
Основные позиционные СС, правила перевода

: 1001

Эта система также используется для записи цветов — красного, зеленого и синего (R, G и B).

Метод преобразования, аналогичный предыдущим, заключается в том, чтобы записать число в виде многочлена с учетом степени 16. Это делается путем деления числа на 16 для получения списка, в котором остаток от деления записан в обратном порядке.

Алгоритм перевода чисел из десятичной в двоичную систему:

1. Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
2. Записать остатки, от последнего к первому.
3. Первый ноль можно не писать.

В Интернете есть калькуляторы, позволяющие конвертировать числа в различные ГЗ (некоторые даже с подробным описанием процедуры).₂

Принципы выполнения простых арифметических операций одинаковы для любой позиционной системы, независимо от основания:<или равен =.

Особенности арифметических СС с различными основаниями:

Примеры арифметических операций:

Для упрощения в различных системах были разработаны готовые таблицы сложения:₁₀.

Дополнение в 8 СС до 16СС

Их можно использовать для быстрого сложения в различных СС.

Сложение для различных СС на примере 15 и 6:

Альтернативный способ преобразования для гуманитариев

Когда нужно сложить числа из разных систем, их приводят к одному основанию. Самый простой способ — перевести в десятичную систему, решить простой пример и перевести результат в любую систему.

Рассмотрим сумму 43

и 56

. Результат можно выразить в любой системе, но проще перевести его в 8 или 16:

Переведите число 56 в двоичную систему в восьмеричной системе счисления:

Шестнадцатеричная СС

Умножение до 8 СС

Как только люди научились считать, возникла необходимость в изобретении чисел.

Для простоты люди стали группировать палочки по 3, 5 или 10 штук. У каждой группы был определенный знак или предмет. Первоначально для нумерации использовались пальцы, так появились первые обозначения для групп из 5 и 10 (единиц). Это позволило создать более удобные системы записи чисел.

Алгоритм преобразования чисел в 16СС

Древнеегипетская десятичная система

В Древнем Египте для обозначения чисел 1, 10, 10 2, 10 3, 10 4, 10 5, 10 6, 10 7 использовались специальные символы (нумералы). Вот некоторые из них:

Арифметика для 2СС

Почему они называются десятичными числами? Как описано выше, люди начали группировать символы вместе. В Египте они решили сгруппировать по 10 и оставить число «1» без изменений. В этом случае число 10 называется основанием десятичной системы, а каждый символ в той или иной степени является представлением числа 10.

В древнеегипетской системе счисления числа записывались в виде комбинации этих символов, каждый из которых повторялся максимум девять раз. Итоговое значение было равно сумме элементов числа. Следует отметить, что этот способ определения величины входит в каждую неположительную систему счисления. Примером может служить число 345:

• при сложении чисел двух 1 в двоичной системе переполняется младший разряд (сумма = или ˃ основания СС), то единица переходит к большему разряду;
• если есть 0-1=1, идет заимствование из старшего разряда;
• умножать 2СС удобнее всего в столбик, учитывая 4 основные правила;
• заем единиц в 2СС при отнимании/делении, тогда она дает промежуточным разрядам по 1, а для занимаемого разряда сразу 11.

Вавилонская шестнадцатеричная система

В отличие от египетских, вавилонские используют только 2 цифры, четный клин для единиц и горизонтальный клин для десятков. Чтобы определить значение числа, нужно разделить изображение числа на цифры справа налево. Новая цифра начинается с появлением прямого клина после обратного клина. В качестве примера возьмем число 32. Число 60 и все его силы обозначаются как «1» таким же образом с помощью прямого клина. По этой причине вавилонскую систему счисления также называют шестнадцатеричной. Вавилоняне записывали все числа от 1 до 59 в неположительной десятичной системе, а большие числа — в положительной системе, основанной на 60. Номер 92: Номер не был уникальным, потому что не было номера для нуля. Представление числа 92 могло означать не только 92 = 60+32, но и, например, 3632 = 3600+32. Для определения абсолютного значения числа был введен специальный символ, обозначающий опущенную шестнадцатеричную цифру, соответствующую появлению цифры 0 в десятичном файле чисел: число 3632 теперь должно записываться следующим образом:

Как упоминалось ранее, первые предпосылки для возникновения позиционной системы исходят из древнего Вавилона. В Индии эта система приняла форму десятичного числа с нулем, и от индийцев эту систему счисления заимствовали арабы, от которых ее переняли европейцы. По какой-то причине европейцы приняли ее как арабскую систему счисления.

Десятичная система счисления

Это одна из наиболее часто используемых систем счисления. Это то, что мы используем, когда мы используем пре

Эта система в основном используется в компьютерных технологиях. Почему они не использовали привычную нам систему 10? Первая счетная машина была разработана Блезом Паскалем, который использовал десятичную систему, что оказалось невыгодным для современных электронных машин, так как необходимо было производить устройства, способные работать в 10 шагов, что увеличивало их цену и конечный размер машины. Эти недостатки устраняются элементами, используемыми во 2-й системе. Однако эта система была разработана задолго до изобретения компьютеров и имеет свои «корни» в культуре инков, где использовались кипу — сложные веревочные сетки и узлы.

Двоичная позиционная нумерация основана на 2 и использует 2 знака (цифры) для записи числа: 0 и 1. В каждом разряде допускается только одна цифра, либо 0, либо 1.₈Примером может служить число 101. Это соответствует числу 5 в десятичной системе счисления. Каждая цифра двоичного числа должна быть умножена на основание «2», которое возводится в степень, равную номеру цифры для преобразования из 2 в 10. Таким образом, число 101₁₆= 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 5

Хорошо, 2-я система счисления более практична для машин, но мы часто видим и используем числа в 10 на компьютере. Как машина определяет число, которое вводит пользователь? Как числа переводятся из одной системы в другую, если они имеют только два знака — 0 и 1?

Компьютер может работать с двоичными числами (кодами), и их нужно где-то хранить. Для хранения каждой цифры используется скремблер — электронная схема. Он может принимать 2 состояния, одно из которых соответствует нулю, а другое — единице. Для хранения одной цифры используется регистр — набор исполнительных механизмов, количество которых соответствует количеству цифр двоичного числа. Набор регистров является функциональной памятью. Число, содержащееся в регистре, является машинным словом. Арифметические и логические операции со словами выполняются арифметико-логическим блоком (ALU). Регистры пронумерованы для упрощения доступа к ним. Это число называется адресом регистра. Например, если нужно сложить 2 числа, достаточно сослаться на номера ячеек (регистров), в которых они находятся, а не на сами числа. Адреса записываются в 8- и 16-битных системах (описанных ниже), так как переход от этих систем к двоичной системе и обратно довольно прост. Для преобразования из 2 в 8 число нужно разделить на группы по 3 цифры справа налево, а для преобразования в 16 число нужно разделить на группы по 4. Если в крайней левой группе цифр есть недостающие цифры, они заполняются крайней левой группой цифр.

Непозиционные системы

Иногда требуется перевести число из одной системы счисления в другую, поэтому давайте рассмотрим, как оно преобразуется между различными системами.

Преобразование в десятичную систему счисления

У нас есть серия

в системе счисления, основанной на b. Для перевода в десятичную систему счисления каждую цифру числа нужно умножить на b n, где n — количество цифр. Таким образом (a

*b 2 + a

*b 1 + a

*b 0 )

Пример: 101

= 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 5

Преобразование десятичных чисел в другие системы счисления

Позиционные системы счисления

Если записать все остатки снизу вверх, то получится сумма 17. 15

= 17

Преобразование из двоичной системы в восьмеричную и шестнадцатеричную

Для перевода в восьмеричную систему счисления — разделите двоичное число справа налево на группы по 3 цифры и заполните недостающие крайние цифры нулями. Затем преобразуйте каждую группу, поочередно умножая цифры на 2 n, где n — количество цифр.₁₀.

В качестве примера возьмем число 1001

: 1001

= 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 11

Для перевода в шестнадцатеричную систему счисления разделите двоичное число справа налево на группы по 4 цифры, а затем выполните аналогичное преобразование от 2 до 8.

Преобразование из восьмеричной и шестнадцатеричной системы в двоичную₂Преобразование восьмеричного числа в двоичное — каждая цифра восьмеричного числа преобразуется в трехзначное двоичное число путем деления на 2. (Подробнее о делении см. раздел «Преобразование десятичных чисел в другие числа»), заменяя недостающие ведущие цифры ведущими нулями.₁₀.

В качестве примера возьмем число 45

: 45 = (100) (101) = 100101₂Преобразование 16 в 2 — Преобразование каждой позиции шестнадцатеричного числа в двоичное четырехзначное число путем деления на 2, заменяя недостающие ведущие биты ведущими нулями.₈Преобразуйте дробную часть любой системы счисления в десятичные числа.₁₆Преобразование выполняется так же, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени «-n», где n начинается с 1.

Перевод из одной системы счисления в другую

Пример: 101.011

= (1*2 2 + 0*2 1 + 1*2 0 ), (0* 2-1 + 1* 2-2 + 1* 2-3 ) = (5), (0 + 0,25 + 0,125) = 5,375

Преобразование десятичных разрядов двоичной системы в 8 и 16₁a₂a₃Дробная часть преобразуется так же, как и целая часть, с той разницей, что дробная часть делится на группы из 3 и 4 цифр справа от десятичной точки, а недостающие цифры дополняются нулями справа.₁a₂a₃)_b= (a₁Пример: 1001,01₂= 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,2₃₁₀.

₂Преобразование восьмеричного числа в двоичное — каждая цифра восьмеричного числа преобразуется в трехзначное двоичное число путем деления на 2. (Подробнее о делении см. раздел «Преобразование десятичных чисел в другие числа»), заменяя недостающие ведущие цифры ведущими нулями.₁₀

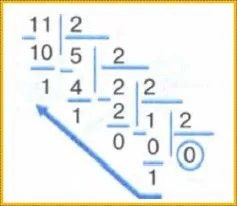
1. Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
2. Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.

1. Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
2. Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

₁₀₈.

₂₂₈

₈₂

₂₁₀

₂₈