Тип переменной определяет диапазон всех значений, которые может принимать конкретная переменная, и операции, которые возможны с ней. Существует несколько предопределенных типов переменных. Типичными типами являются числовые, литеральные и логические типы.
Что такое алгоритм в информатике
Понятие алгоритма является одним из фундаментальных понятий вычислительной математики и информатики.
Алгоритм — это строго определенная последовательность действий исполнителя, которая приводит к конкретной цели или результату за конечное число шагов.
Каждый алгоритм пишется с учетом возможностей исполнителя и учитывает его возможности. Исполнитель — это субъект, который способен выполнить определенный набор инструкций. Набор инструкций, которые исполнитель может понять и выполнить, называется системой инструкций исполнителя.
Чтобы выполнить алгоритм, исполнителю нужен не только сам алгоритм. Выполнить алгоритм — значит применить его для решения конкретной задачи, т.е. выполнить запрограммированные действия по отношению к конкретным входным данным. Поэтому исполнителю необходимы исходные (входные) данные — набор данных перед запуском алгоритма.
В результате выполнения алгоритма исполнитель должен получить желаемый результат — выходные данные, которые исполнитель извлекает в результате выполнения задания. При выполнении задания исполнитель может генерировать и использовать данные, которые не являются выходными данными — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное представление шагов алгоритма на естественном языке имеет свои недостатки. Вербальные описания не могут быть строго типизированы, поэтому свойство определенности алгоритма может быть нарушено: Исполнитель может не совсем точно понять описание шагов алгоритма. Словесные обозначения довольно длинные. Сложные задачи трудно представить в словесной форме.
Пример 1. Запишите правило деления дробей в словесной форме.
Решение. Шаг 1 Умножьте числитель первой дроби на знаменатель второй дроби. Шаг 2 Умножьте знаменатель первой дроби на числитель второй дроби. Шаг 3. Запишите дробь, в числителе которой будет результат шага 1, а в знаменателе — результат шага 2.
Описанный выше алгоритм может быть применен к любым двум дробям. Вы получаете выходные данные — результат деления двух дробей (исходные данные).
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущих к цели, можно считать алгоритмом. Поиск пищи животным — это алгоритм; движения робота также описываются алгоритмом.
В узком смысле, в котором этот термин используется в информатике, алгоритмы применяются программистами, некоторыми инженерами и аналитиками, а также специалистами по машинному обучению, контроллерами и многими другими. Это одно из ключевых понятий в компьютерной науке.
Для чего нужны алгоритмы
Алгоритмы необходимы в компьютерной науке для эффективного решения различных проблем, в том числе тех, которые являются очень сложными или которые невозможно решить «в лоб». На практике существуют алгоритмы практически для всего: сортировки, обхода структур данных, поиска данных, фильтрации информации, математических операций и так далее.
Например, вы можете отсортировать таблицу с помощью полнотекстового поиска — это самое очевидное решение. Или вы можете использовать алгоритм быстрой сортировки: Он более сложный и не такой очевидный, но он гораздо быстрее и не потребляет так много компьютерной энергии. Строго говоря, грубая сила — это тоже алгоритм, но очень простой алгоритм.
Существуют алгоритмически неразрешимые проблемы, для которых нет и не может быть алгоритма. Однако большинство задач в информатике можно решить с помощью алгоритмов, и алгоритмы активно используются в работе с ними.
Алгоритмы используются во всех областях информатики и во многих других дисциплинах. Инструкции для автоматической машины или производственной линии являются алгоритмами, как и рецепт. Поэтому алгоритмы необходимы для всего.
Свойства алгоритмов
Дискретность. Алгоритм не является единой неделимой структурой, а состоит из отдельных небольших шагов или действий. Эти действия выполняются в определенном порядке, каждое из них начинается после завершения другого.
Эффективность. Выполнение алгоритма должно привести к определенному результату и не должно оставлять неопределенности. Результат может быть неудачным — например, алгоритм может сообщить, что решения нет — но оно должно быть.
Детерминизм. Ни на одном этапе не должно быть двусмысленности или непоследовательности; инструкции должны быть четко определены.
Массивность. Алгоритм обычно можно распространить на аналогичные задачи с другими начальными данными — при условии, что вы измените начальные условия. Например, типичный алгоритм решения квадратного уравнения остается неизменным независимо от чисел, используемых в уравнении.
Ясность. Алгоритм должен содержать только те действия, которые известны и понятны исполняющему его человеку.
Совершенство. Алгоритмы конечны; они должны завершиться за определенное количество шагов и выдать результат, соответствующий определенным определениям.
Виды и типы алгоритмов
Линейный алгоритм — это последовательное выполнение инструкций в строгом порядке (например, «сделать бутерброд с сыром»).
- взять кусок хлеба;
- отрезать кусок сыра;
- положить его на хлеб.
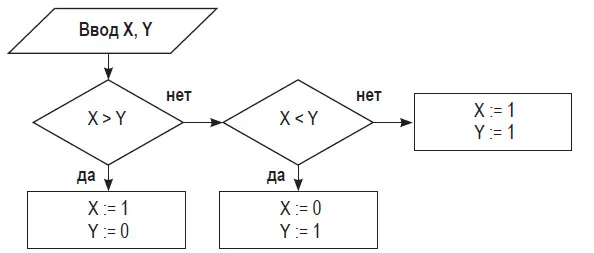
Ветвь — это последовательность действий в соответствии с определенными условиями (если выполняется одно условие, выполняется действие 1, если выполняется другое условие, выполняется действие 2),
Пример: Если идет проливной дождь, возьмите зонтик, в противном случае не берите зонтик.
В большинстве случаев слово «иначе» опускается, поскольку дальнейшая логика уже следует из контекста первой части предложения.
Пример: Если вы хотите сообщить что-то важное, позвоните (в этом случае, конечно, нет причин звонить, если сообщение неважное).
Циклические алгоритмы — это последовательности действий, которые необходимо повторить несколько раз для достижения положительного результата («груши на
В математике и информатике — это поиск эффективного решения поставленной задачи с помощью инструментов и приборов.
- взять из ящика грушу;
- посмотреть, гнилая она или нет;
- если гнилая, то выбросить;
- если нет, положить в другой ящик;
- повторить операцию до перебора всех груш в ящике.
Даже при решении простой задачи (2*6) используются определенные методы и инструменты для получения правильного результата. Самое интересное в нем то, что его можно решать по-разному: с помощью листа бумаги и карандаша, вычисляя на компьютере или умножая в уме. В этом случае лучшим алгоритмом будет самый эффективный способ решения проблемы.
Но такие простые примеры не очень интересны для энтузиастов компьютерных наук. Есть гораздо более интересные проблемы, которые увлекают многих программистов, и ученые всего мира стремятся их решить.
Есть и другие интересные примеры понимания сложности алгоритмов. Например, задача о путешествующем продавце.
Продавец должен посетить четыре города: Москва, Берлин, Лондон и Сан-Франциско. Он должен продать там, а потом вернуться.
Решение проблемы кажется простым. Сначала отправляйтесь из Москвы в Берлин, затем в Лондон, потом в Сан-Франциско и обратно в Москву.
Где применяют алгоритмы
Фактически, это сложный алгоритм для компьютера. В этих 4 вариантах скрыты 24 различные комбинации поездок для решения проблемы. Компьютер рассчитывает расстояние от одного города до другого, затем сравнивает варианты и выдает решение.
Однако если увеличить количество городов (например, до 100), компьютер не сможет решить задачу, потому что вариантов миллионы, и на решение проблемы уйдет несколько столетий.
Но самое интересное, что принцип решения такой задачи можно распространить на все задачи подобного рода, что расширит знания в информатике (что это такое?) и других науках.
Задача продавца (коммивояжера)
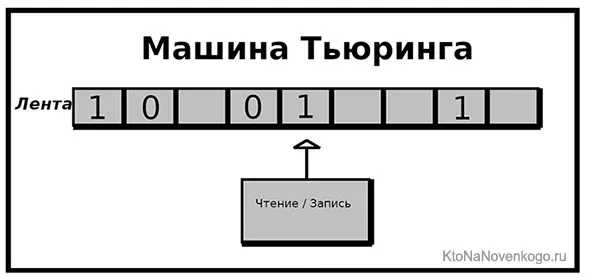
Это абстрактная машина, изобретенная Аланом Тьюрингом, знаменитым британским ученым. Гениальность этой машины заключается в следующем. Существует вид ленты, состоящей из множества отдельных (бесконечных) ячеек, содержащих данные или биты (0 и 1). Имеется считывающее устройство, которое имеет доступ к ленте.
По мере движения машина получает определенные инструкции, обращается к ячейкам, считывает информацию и продолжает работу. Но машина может изменить свои действия, записать другую информацию или двигаться в том или ином направлении (на основе стека внутренних инструкций).

В результате исследования таких машин Тьюринг предположил, что алгоритм нахождения значений функции, заданной в алфавитном поле, существует только в том случае, если эта функция вычисляется машиной Тьюринга.
Это требование
Чтобы понять эту концепцию, необходимо знать свойства алгоритма в информатике. Их несколько:
Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задачи путем выполнения простых шагов. Чтобы решить задачу с помощью алгоритма, решение должно быть основано на принципе простоты; в то же время на шаги должно быть отведено определенное время. Каждый шаг должен определяться состоянием системы, т.е. если входные данные одинаковы, то результат не меняется. Однако существуют и вероятностные алгоритмы, в которых баллы зависят от системы и от случайно сгенерированных чисел. В этом случае концепт становится подвидом обычного концепта.
Машина Тьюринга — это основа для понимания алгоритмов
Концепция заключается в том, что инструкции алгоритма должны быть доступны конкретному исполнителю и принадлежать персоналу системы. В ходе выполнения задания, если входные данные верны, математическая функция выдает результат за определенное количество шагов. Иногда процесс может дать сбой, но вероятность таких случаев стремится к нулю.
Универсальность или массовость позволяет использовать алгоритм с различными наборами входных данных. Последнее свойство обеспечивает завершение в виде конкретного числа — результата.
Каждый алгоритм имеет свои начальные условия, цели и способы решения задачи. Существует большая разница между расчетными формулами и интерактивными формулами. Происхождение первого термина восходит к экспериментам ученого Тьюринга, который смог преобразовать входные данные в выходные. Последние предназначены для связи с объектом управления и работают только под внешним воздействием. В информатике различают несколько типов алгоритмов:
Жесткие также называют механическими, поскольку они обычно используются для управления двигателем или машиной. Они определяют действия в единой правильной последовательности, которые приведут к желаемому или требуемому результату при выполнении процедур, для которых они разработаны.
Выводы
Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются в различных умственных рассуждениях без строгих аргументов, а вторые позволяют вывести результат различными способами.
- «действие» можно использовать для создания алгоритма;
- «действие» может быть элементарным;
- «действие» может быть реализовано алгоритмом;
- в «действии» обязательно участвует некоторый объект или группа объектов;
- для группы объектов «действие» происходит только тогда, когда эти объекты «достаточно близко»;
- в действии изменяются связи и параметры объектов (включая параметры их движения);
- «действие» всегда и обязательно должно быть повторимо.
Линейная формула — это серия инструкций, выполняемых в строгом порядке. Ветвь содержит как минимум одно условие и при проверке приводит к разделению на несколько блоков. Показаны альтернативные типы программ разветвления.
В циклических типах одни и те же действия повторяются несколько раз, изменяя входные данные. Это также относится к вариантам и большинству методов расчета. Цикл — это последовательность A
Проделайте то же самое со всеми числами. Первые четыре шага повторяются непрерывно. Если найдено число, которое не является простым (4, 6, 8 и т.д.), его нужно пропустить. Алгоритм в этом случае является условным, т.е. проверки выполняются в начале цикла.
Свойства и виды
Распространение информационных технологий увеличило риск провала программы. Избежать ошибок в алгоритмах можно, доказав их правильность математическими средствами. Такой анализ называется формальным методом и требует использования определенного набора инструментов.

- дискретность;
- детерминированность или определенность;
- понятность;
- завершаемость или конечность;
- массовость или универсальность;
- результативность.
Гипотеза Ричарда Мейса гласит, что легче избежать ошибок, чем устранить их. Доказывая корректность программ, можно определить их свойства, которые применимы ко всем типам входных данных. Сам термин различают в двух вариантах: частичный и полный. В первом типе корректности алгоритм выдает правильный результат только для тех случаев, в которых он завершается. Во втором случае программа завершается корректно для всего диапазона данных.
Исполнители сравнивают выходной сигнал с конкретным желаемым результатом во время теста. Для доказательства корректности используются предусловия и постусловия. Первое должно быть выполнено до начала программы, второе — после ее завершения. Формальные методы успешно применяются для решения многих задач: Проверка программ и микропроцессоров, разработка искусственного интеллекта, электронные схемы и автоматические системы для железных дорог, спецификация стандартов.
Для выполнения алгоритма требуется лишь определенное количество шагов, но на практике это занимает много времени. Именно поэтому было введено понятие сложности. Это может относиться к времени, вычислениям и размеру. Для повышения эффективности используются быстрые программы, которые появились еще в 1950-х годах.
- детерминированные или жесткие;
- гибкие;
- линейные;
- разветвляющиеся;
- циклические;
- вспомогательные;
- структурные блок-схемы.



- сначала нужно взять число 1;
- проверить, меньше ли оно, чем 100;
- если да, то узнать, простое ли оно;
- при выполнении условия записать;
- перейти к числу 2;
- повторить операцию.
Анализ работы