Происхождение непозиционных систем счисления уходит корнями в глубокую древность. Древние народы, такие как Вавилон, майя, Древний Египет, Греция и Рим, использовали системы нумерации без позиции. Некоторые из этих систем, например, латинские цифры, используются и сегодня.
Непозиционные системы счисления
Привет. На этой странице мы рассмотрим одну из самых важных тем в информатике — непозиционные системы счисления. Здесь вы узнаете, что такое нестатистические системы и основные определения, применимые к этой теме. Мы также рассмотрим, чем они отличаются от позиционной нумерации, а также преимущества и недостатки.
Позиционно-независимые системы счисления — это системы, в которых положение цифры в числе (позиция цифры) не влияет на его значение.
Чтобы понять, что именно имеется в виду, давайте выберем наиболее распространенную систему счисления — десятичную. Все это знают. Им пользуются люди в большинстве стран мира. Алфавит десятичной нумерации состоит из арабских символов — цифр от 0 до 9. Это позиционная система счисления. Почему, спросите вы? Все очень просто. В качестве примера возьмем два числа, 1000 и 10. Посмотрите на цифру один — в зависимости от того, какое место она занимает в числе, меняется значение, которое она обозначает. Число 1000 содержит тысячи, а 10 — десятки.
Это не относится к непозитивным представлениям. В качестве примера возьмем латинскую нотацию. Вы видели его и знакомы с ним. Помните, что он используется в учебниках истории для обозначения веков и количества монархов. Например, Петр I или Иван IV Грозный. Примечание I и IV записаны как 1 и 4 на арабском языке. Здесь значение единицы не меняется в зависимости от того, какую позицию она занимает. Неважно, будет ли это первая или вторая позиция.
Историки предполагают, что вычисления, так называемые позитивные вычисления, уходят корнями в глубокую древность, в самые ранние формы измерения, используемые человеком. Давайте теперь поговорим об их типах и рассмотрим их недостатки.
Примеры непозиционных систем счисления
Унарная непозиционная
Его также называют неположительным единственным числом. Вы, наверное, уже догадались, почему он так называется. Это связано с тем, что в данной форме записи используется только один символ. Это представление использовали еще древние. Для записи значений использовались насечки на костях животных или стенах пещер. Также использовались зарубки в дереве. Он используется и сегодня. Помните сериал, где заключенные считают дни в неволе. Он также используется для обучения детей счету — так называемый пальцевый метод.

Унарные ss — метки на кубиках
Римская непозиционная
Мы уже упоминали об этом выше. Они
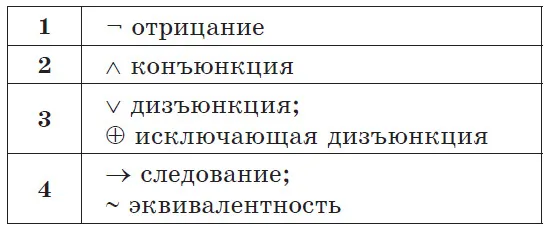
Она берет свое начало в третьем тысячелетии до нашей эры. Все значения были записаны здесь иероглифами. Не было никаких специальных правил — все числовые значения просто складывались вместе. Также не было правил написания — последовательность могла быть написана как слева направо, так и справа налево. Персонажи могут занимать любые позиции. Ниже приведена таблица со значениями некоторых из них.
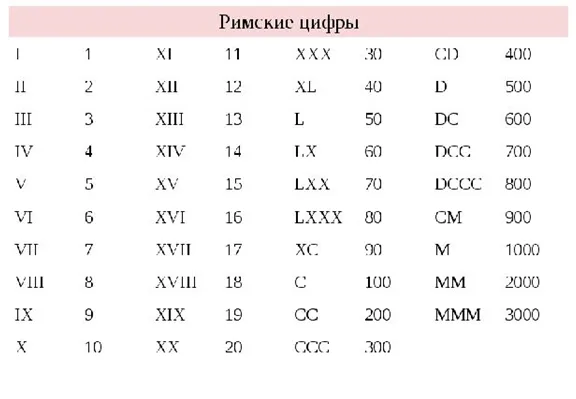
Египетская непозиционная
Стоит обратить внимание на эти формы письма. Здесь все очень просто — каждой букве алфавита соответствует цифра. Стоит отметить, что эти неположительные системы являются более продвинутыми, чем все предыдущие, поскольку в них были ссылки на десятки и сотни. Среди недостатков — их сложность. Можно выбрать два популярных примера.
Алфавитные системы счисления
Его использовали еще наши предки в Древней Руси. Первое упоминание о нем в летописях прошлых времен относится к началу десятого века. Каждая буква глаголической письменности соответствовала цифре. Во времена Российской империи в 18 веке она перестала использоваться в полном объеме и была заменена десятичной системой счисления. Мы используем его и сегодня.
Славянская
Его также называют непозитивным современным греческим или ионическим письмом. Доказательства восходят к третьему веку до нашей эры. Здесь он считался с буквами, используемыми в латинской графике. Оно заменило старую греческую форму. Непозитивное кириллическое представление фактически является его копией.

Греческая
Неположительная — это система, в которой число представлено набором узловых и алгебраических чисел. Положение цифры не имеет значения.
Непозиционные системы счисления
Неположительная система была одной из первых, которую использовали люди. Самая древняя из них — египетская (2,5-3 тысячи лет до нашей эры). Содержащиеся в нем числа были написаны иероглифами, которые подчинялись «принципу сложения». Греческая, римская и другие древние системы нумерации имели аналогичный принцип.
В древнеегипетской системе счисления в качестве цифр использовались единицы и десятичные числа: 10, 100, 1000 и так далее.
Виды
Древнеегипетская система
Поэтому написание цифр в этой системе было еще длиннее, чем в римских цифрах:
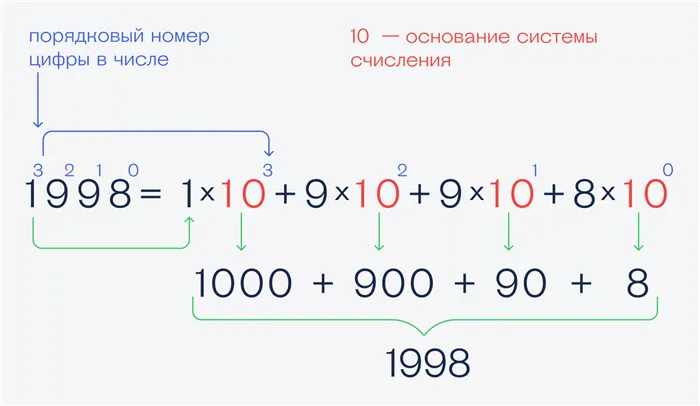
Латинские цифры знакомы всем со школы. Алфавит этой системы счисления состоит из цифр 1, 5 и ряда десятичных дробей:

Римская система
Эти простые числа (узловые числа) используются для записи других чисел путем сложения или вычитания меньшего числа из большего. Числа I, X, C, M не должны повторяться более трех раз, а V, L, D не должны быть последовательными.
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
| I | V | X | L | C | D | M |
Запись больших чисел в этой системе кажется громоздкой:
2589 = 2000 + 500 + 500 + 80 + 9 = MM + D + LXXX + IX = MMDLXXXIX.
Чтобы правильно их прочитать, нужно мысленно разделить их на цифры.
Этот способ нумерации в Древней Греции был основан на алфавите, похожем на латинский алфавит
Древнегреческая система
В математике в настоящее время существует две системы неположительных чисел — биномиальная система чисел и система классов остатков. Оба они зависят от вычислительных алгоритмов, и понимание того, чем они отличаются от локальных систем, значительно облегчит работу с ними.
| 1 | 5 | 10 | 100 | 1000 | 10000 |
| I | Г | Δ | H | X | M |
Биномиальная система счисления существует, когда число представляется в виде суммы биномиальных коэффициентов. Слово «биномиальная» означает, что система основана на биномиальной системе Ньютона — методе, с помощью которого одни числа могут быть разложены на другие.

Эта система чисел используется в комбинаторике — с ее помощью можно быстро вычислить нужную комбинацию, не перебирая все предыдущие варианты. Это также используется для тестирования программного обеспечения, контроля качества и анализа лотерей — выявляются комбинации и сочетания факторов, которые, скорее всего, могли привести к каким-то значительным результатам.
Перевод десятичного числа в римское
Система категорий остатка основана на модульной арифметике, где числа сравниваются по модулю (если они дают одинаковый остаток при делении). Там все состоит из баз, модулей и похоже на работу с таблицами. Благодаря свойству, что некоторые вычисления имеют только одно решение, система остаточных классов используется в информационной безопасности, проверке ошибок и обеспечении надежности космической или военной техники.
- Берём самое большое римское число и смотрим, наше число больше или нет.
- Если наше больше — вычитаем из нашего римское и записываем его.
- Если не больше — переходим к следующему римскому.
- Так делаем до тех пор, пока у нас в остатке не получится ноль.
- 1998 и 1000 (M) — самое большое римское число. Наше больше, поэтому отнимаем и добавляем новую букву: M. Остаток — 998
- Снова проверяем с самым большим числом — 1000 (M). Наше число меньше, поэтому берём следующее: CM (900). Это уже подходит, поэтому вычитаем его из 998: 998 − 900 = 98. Запоминаем остаток и добавляем CM к нашему числу: MCM
- Берём остаток — 98 — и проверяем снова все римские числа сверху вниз. Первое римское число, которое меньше нашего, — это XC (90). Отнимаем, получаем остаток 8 и добавляем XC к нашему числу: MCMXC
- Берём остаток — 8 — и смотрим, какое минимальное римское число меньше него, это V (5). Отнимаем пятёрку, получаем 3 и добавляем V к римскому числу: VCVXCV.
- Из числа 3 последовательно отнимаем три единицы I (1), и дописываем их к римскому числу: MCMXCVIII.
- У нас в остатке 0, а значит, мы закончили с переводом. 1998 = MCMXCVIII.