Рассеяние света также характеризуется ГК. В процессе рассеяния света участвуют фазовые скорости и преломление в абсолютных значениях. Теория была открыта Ньютоном в 1672 году.
Колебания в природе
Вокруг нас существуют различные вибрации. Большинство движений в природе, даже направленных, имеют, по крайней мере, небольшой компонент колебаний.

Колебания различают периодические (волны, маятник) и непериодические (флаг на ветру). Главное отличие между ними заключается в том, что каждое периодическое колебание очень похоже по своим характеристикам на предыдущее и последующее. Изучение непериодических колебаний показывает, что каждое из них может быть представлено бесконечной суммой периодических колебаний. Поэтому описание любого колебательного процесса основано на описании периодических колебаний.
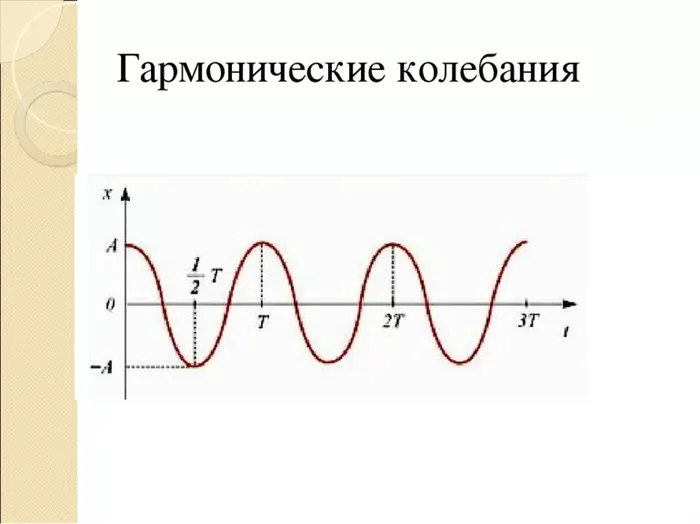
Гармонические колебания и их закон
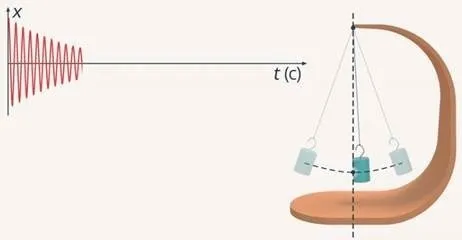
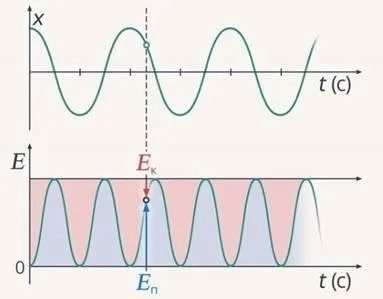
Изучение колебаний должно начинаться с построения их графика. Время $t$ откладывается по оси абсцисс, а отклонение $x$ — по оси ординат. Используется маятник с песком или цветным порошком, приводится в колебание и под ним расстилается лист, на котором остается след.
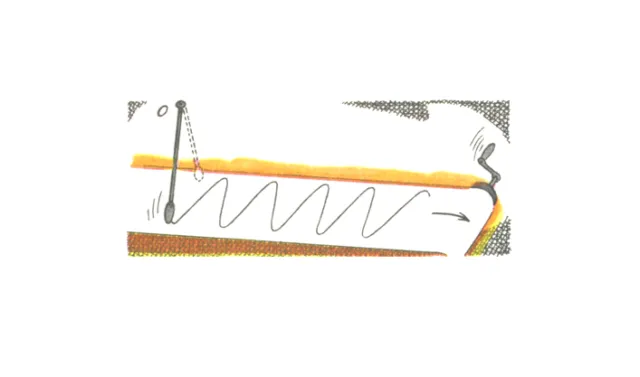
Кратко напомним, что причиной колебаний маятника является равновесие, которое равно нулю в среднем и максимуму в крайних положениях и направлено против отклонения. Ускорение маятника не меняется.
Теория высшей математики доказывает, что единственной функцией, ускорение которой пропорционально отклонению и направлено против отклонения, является синус $x=A sin(\omega t+\phi)$.
Если мы посмотрим на след, оставленный маятником на натянутом лезвии, то увидим график именно этой функции.
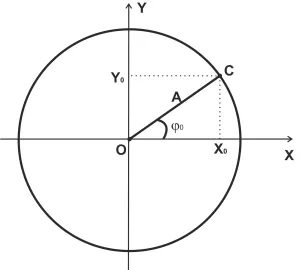
Колебание, подчиняющееся закону синуса, называется гармоническим колебанием. В приведенных выше формулах параметр $A$ называется амплитудой, параметр $\omega$ — частотой (иногда циклической частотой), а параметр $\phi$ — фазой (иногда начальной фазой). Хорошими примерами гармонических колебаний являются также водяные волны, движение груза на пружине или движение поршня в двигателе автомобиля.
Параметры гармонического колебания
Формула гармонического колебания включает три параметра.

- Ширина $A$характеризует «размах» колебания. Разность амплитуд колебаний (при прочих равных) означает разность наибольшего отклонения, которое наблюдается у исследуемых явлений. Маятник с большей амплитудой будет качаться на большее отклонение, хотя пройдет точку равновесия одновременно с маятником, у которого амплитуда меньше.
- Частота $\omega$характеризует «скорость» колебания. Разность частот означает разность количества колебаний в единицу времени (при прочих равных). Маятник с вдвое большей частотой совершит два колебания за время одного колебания другого маятника, хотя амплитуда при этом будет одинакова.
- фаза $\phi$характеризует «положение в начальный момент». Разность фаз означает, что исследуемые процессы находятся в различных состояниях в один момент времени, одно колебание может проходить точку равновесия, а другое в это время будет в точке максимального отклонения. Маятники с разными фазами (при прочих равных), будут отклоняться на одну и ту же величину, и число колебаний за одно и то же время у них будет одинаково. Но при этом они всегда будут в разных состояниях, один маятник будет постоянно «догонять» другой.
Определение гармоники для колебаний появилось в глубокой древности в связи с изучением музыкальной гармонии, когда стало ясно, что движение вибрирующей струны может быть хорошо описано законом синуса.
Гармонические колебания. Амплитуда, период и частота колебательного движения

В данном курсе рассматривается простейший вид колебательного движения — гармонические колебания. Рассматриваются основные характеристики колебательного движения: Амплитуда, период (частота) и фаза.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам, вам необходимо добавить их в свой личный шкафчик.
2. Распространите видеоуроки в своих личных кабинетах среди учеников.
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Гармонические колебания. Амплитуда, период и частота колебательного движения»
Мы говорили об этом в теме прошлой недели.
Гармонические колебания — это колебания, при которых смещение точки колебания от положения равновесия изменяется со временем по закону синуса или косинуса.
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называются кинематическим законом гармонического движения.
Мы хотим показать, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую схему.
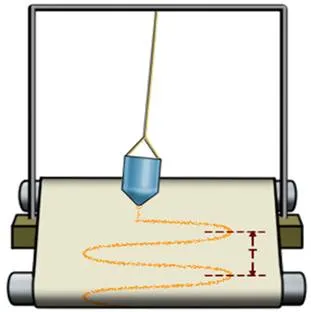
Возьмем маятник с нитью, возьмем небольшой твердый контейнер с маленьким отверстием в дне и наполним его песком, а под полученную систему поместим длинную бумажную ленту.
Если лента движется с постоянной скоростью перпендикулярно плоскости колебаний, она оставит волнистый песчаный след, каждая точка которого соответствует положению колеблющейся массы в тот момент, когда она его пересекла. Из опыта мы знаем, что след, оставленный песком на листе бумаги, является своего рода кривой.
Это называется синусоидальной волной. Из уроков математики в школе вы знаете, что подобные графики имеют функции типа.
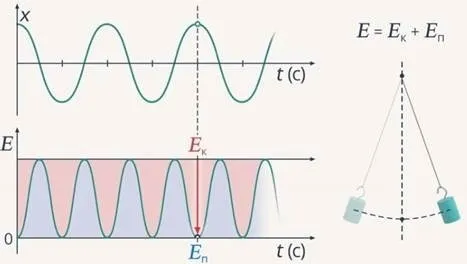
Таким образом, зависящее от времени смещение точки вибрации графически представляется в виде синуса или косинуса.
Ось времени t проходит через точки, соответствующие положению равновесия маятника, а ось смещения x проходит перпендикулярно ей. График позволяет приблизительно определить координату груза в каждый момент времени.
Теперь разберемся с величинами, содержащимися в уравнении колебательного движения.
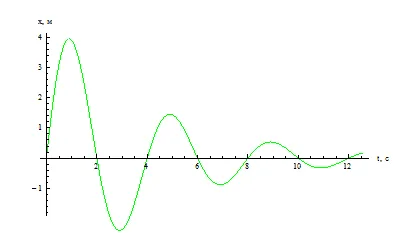
Но принудительное колебание пополняет запас энергии за счет внешнего воздействия. Если это происходит каждый период, то колебания вообще не затухают.
Вынужденные колебания — это колебания, возникающие под воздействием внешней, периодически изменяющейся силы.
Частота, с которой действует эта сила, равна частоте, с которой система будет колебаться.
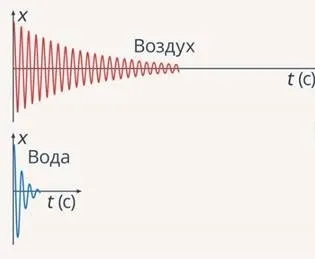
Например, качели. Если кто-то замахивается на вас, и вы получаете толчок каждый раз, когда попадаете в одну и ту же точку, такой замах считается вынужденным.
Этот замах также считается вынужденным, если вы раскачиваетесь из положения равновесия. Только в этом случае амплитуда (о которой речь пойдет ниже) увеличивается с каждым взмахом.
Вынужденные колебания
Выполняйте физические упражнения в течение 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.
Иногда для вынужденного промедления не нужно внешнего воздействия. Существуют системы, в которых это внешнее воздействие возникает само собой благодаря способности регулировать поток энергии из постоянного источника.
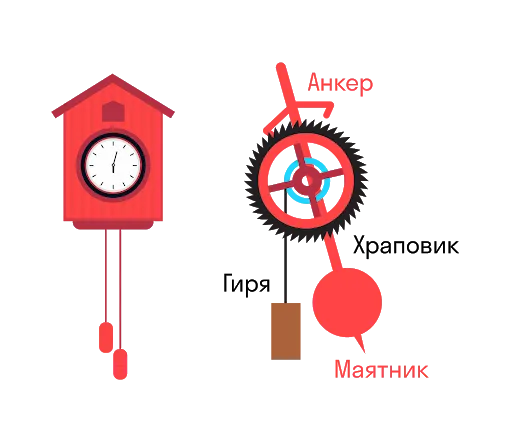
Автоматическая система осцилляции состоит из трех важных элементов:
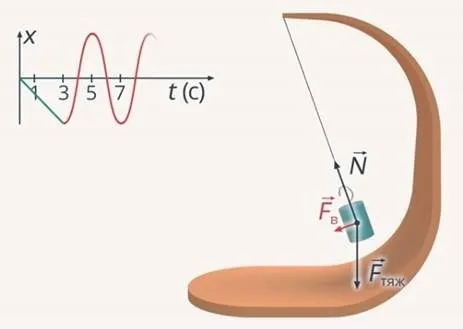
Часы с кукушкой являются примером колебательной системы. Груз на струне (цепи) стремится повернуть зубчатое колесо (щеколду). Когда маятник раскачивается, щеколда зацепляется за шарнир, и вращение приостанавливается.
Однако это придает маятнику толчок, который компенсирует потерю энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается,

Автоколебания
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Характеристики колебаний