Ускорение рассчитывается путем деления метров в секунду (м/с) на секунды (с). Деление расстояния на время равно делению расстояния на квадрат времени. Поэтому единицей СИ ускорения являются метры в секунду в квадрате (м/с²). Чтобы изучение физики было увлекательным, в таблице можно увидеть несколько интересных примеров.
Ускорение – среднее, мгновенное, тангенциальное, нормальное, полное.
Ускорение описывает степень изменения скорости.
Например, автомобиль, который начинает двигаться, движется все быстрее и быстрее по мере увеличения его скорости. В начальной точке скорость автомобиля равна нулю. Как только автомобиль начинает движение, он разгоняется до определенной скорости. Если необходимо затормозить, автомобиль не может остановиться сразу, а только через определенное время. Это означает, что скорость автомобиля стремится к нулю — автомобиль медленно начинает двигаться, пока не остановится. Но физика не знает условий для замедления. Когда тело движется, уменьшая свою скорость, этот процесс также называется ускорением, но со знаком «-«.
Среднее ускорение.
Среднее ускорение — это отношение между изменением скорости и промежутком времени, в течение которого произошло это изменение. Среднее ускорение рассчитывается по следующей формуле
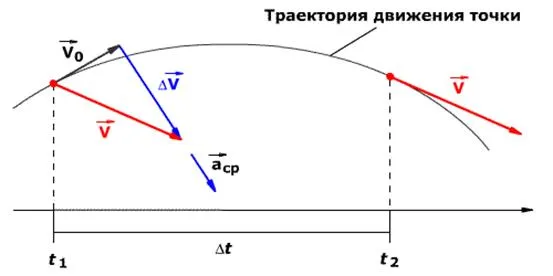
где — вектор ускорения. Направление вектора ускорения совпадает с направлением изменения скорости D — 0
где 0начальная скорость. В момент времени t1(см. рисунок ниже) тело имеет 0 .. В момент времени t2тело имеет скорость = .0. Из этого мы вычисляем ускорение:
В системе СИ единицей измерения ускорения является 1 метр в секунду в секунду (или метр в секунду в квадрате):
Метр в секунду в квадрате — это ускорение линейно движущейся точки, при котором скорость этой точки увеличивается на 1 м/с за 1 с. Другими словами, ускорение определяет степень изменения скорости тела за 1 с. Например, если ускорение равно 5 м/с2, это означает, что скорость тела увеличивается на 5 м/с.
Мгновенное ускорение.
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, которая соответствует пределу, к которому стремится среднее ускорение, когда интервал времени стремится к 0. Другими словами, это ускорение, которое тело развивает за очень короткий промежуток времени:
Ускорение имеет то же направление, что и изменение скорости D X, aY, aZ).
При ускоренном линейном движении скорость тела увеличивается по модулю, т.е. v2>v1а вектор ускорения имеет то же направление, что и вектор скорости 2.
Если скорость тела увеличивается по модулю (v2
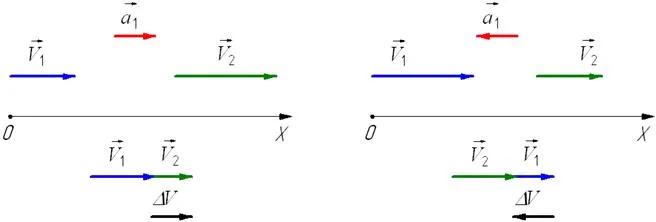
Если движение происходит по криволинейной траектории, то мера и скорость движения одинаковы.
Траектория, радиус-вектор, закон движения тела
Теперь мы рассмотрим простейшую кинематику — кинематику точки. Представим, что тело (материальная точка) движется. Независимо от того, что это за тело, мы все равно относимся к нему как к материальной точке. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы выбросили в окно. Было бы еще лучше, если бы это был новый автомобиль, на котором мы отправляемся в путешествие. Когда мы перемещаемся из точки A в точку B, наша точка описывает воображаемую линию, называемую траекторией. Другое определение траектории — одограмма радиус-вектора, которая представляет собой линию, описываемую краем радиус-вектора материальной точки по мере ее движения.
Радиус-вектор — это вектор, указывающий положение точки в пространстве.
Чтобы узнать положение тела в пространстве в определенный момент времени, необходимо знать закон движения тела — зависимость координат (или радиус-вектора точки) от времени.
Тело переместилось из точки А в точку Б. В этом случае смещение тела — отрезка, непосредственно соединяющего эти точки, — является векторной величиной. Расстояние, которое проходит тело, является длиной его траектории. Понятно, что смещение и путь не следует путать. Мера вектора перемещения и длина пути совпадают только в случае линейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение и путь
Смещение равно разности между радиус-векторами в начальный и конечный моменты времени. Другими словами, это увеличение радиус-вектора.
Средняя скорость — это векторная физическая величина, которая соответствует отношению между вектором перемещения и интервалом времени, в течение которого произошло перемещение.
Теперь представим, что временной интервал уменьшается, сокращается, становится совсем коротким и стремится к нулю. В этом случае нельзя говорить о средней скорости, но скорость становится мгновенной. Любой, кто помнит основы математического анализа, сразу поймет, что без производной нам не обойтись.
Скорость и ускорение
Мгновенная скорость — это векторная физическая величина, равная производной от радиуса вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду.
Если тело движется не равномерно и не прямолинейно, оно имеет не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) — это векторная физическая величина, вторая производная радиус-вектора по времени и, таким образом, первая производная мгновенной скорости.
Ускорение показывает, насколько быстро изменяется скорость тела. С е
$\begin a=\left(\ddot-r \dot^ \sin ^ \theta-r \dot^
ight)^+(2 \dot \dot \dot \dot \sin \theta+r \ddot \sin \theta+2 r \dot \dot \dot \dot \dot \cos \theta)^^^right. \ +\left(2 \dot \dot \sin \theta+r \ddot-2 r \dot^ \sin \theta \cos \theta
ight)^ \frac(13) \end $.
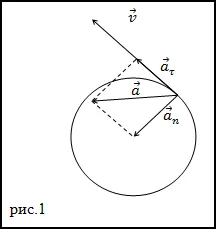
Задание. Материальная точка движется по окружности (рис. 1) радиуса R=2m, уравнение движения. Какова мера ускорения этой точки при t=3 c?
Решение. Используйте формулу в качестве основы для решения задачи:
Формула ускорения в разных системах координат
Используя приведенное уравнение движения, определите меру скорости материальной точки:x,ay,azДифференцируя уравнение модуля скорости (1.2) по времени, получим тангенциальную составляющую ускорения:
Чтобы вычислить нормальную составляющую скорости нашей материальной точки, используем выражение (1.2):
Выражение (1.1) можно использовать для расчета требуемого ускорения:
Ответ. $a=\\\\ около 13,5$ м/с 2
Проверенные авторы готовы помочь вам написать работу любой сложности
Примеры решения задач
Мы уже помогли 4 396 студентам и школьникам справиться с заданиями от решения задач до магистерской диссертации! Определите стоимость вашего задания за 15 минут!
Задание. Какова временная зависимость ускорения материальной точки (a(t)), когда частица движется вдоль оси x, а ее скорость изменяется согласно уравнению: $v=\alpha \sqrt$, где $\alpha$ — постоянная больше нуля? В начальный момент времени (t = 0 с) материальная точка находилась в начале координат (x = 0 м). Постройте график a(t).
Решение. Из условий задачи можно написать, что:
Используя формулу (2.1), определите зависимость координаты x от времени (x(t) ).
ightarrow \alpha t=2 \sqrt+C(2.2)$
где мы определяем константу интегрирования из начального условия задачи. Мы знаем, что x(0)=0, поэтому C=0. Тогда имеем:

Используйте формулу, чтобы найти ускорение для нашего случая (движение вдоль оси x):
мы получаем выражение для a(t):
Ускорение $ не зависит от времени, поэтому график a(t) имеет вид (рис. 2).
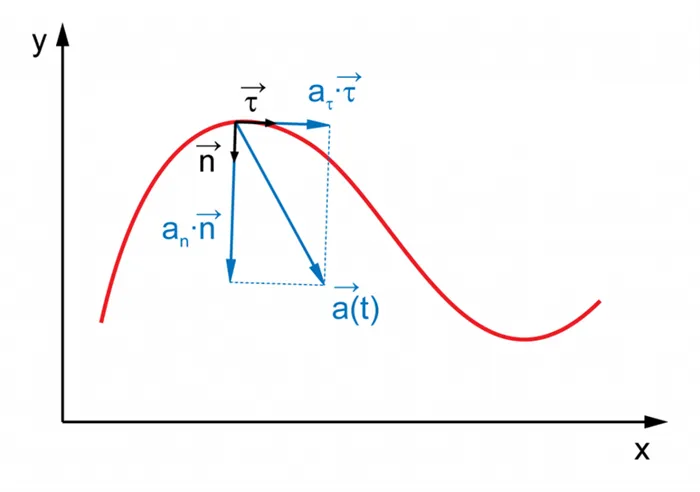
Тангенциальное ускорение — это компонент вектора ускорения, направленный по касательной к траектории в конкретной точке пути движения. Тангенциальное ускорение описывает изменение модуля скорости при криволинейном движении.
Рисунок 1.10. Ускорение траектории.
$\int \alpha d t=\int \frac>Направление вектора тангенциального ускорения (см. рис. 1.10) равно или противоположно направлению линейной скорости. То есть вектор тангенциального ускорения находится на той же оси, что и тангенциальная окружность, которая представляет собой траекторию движения тела.
Нормальное ускорение — это компонент вектора ускорения, который лежит вдоль
Ответ. $a(t)=\frac>