Максимальную высоту подъема можно легко определить из уравнения движения для равновесного движения, если известно время подъема тела и то, что скорость тела в верхней части траектории равна нулю.
Определение скорости свободного падения
Свободное падение тела — это его равновесное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут действовать на тело, либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист выпрыгивает из самолета, первые несколько секунд после прыжка он находится в свободном падении. Этот короткий период времени характеризуется ощущением невесомости, подобным тому, которое испытывают астронавты в космическом корабле.
Ученые знали о свободном падении еще в Средние века: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Они утверждали, например, что скорость падающего тяжелого предмета увеличивается прямо пропорционально пройденному расстоянию. В 1545 году испанский ученый Д. Сото исправил эту ошибку, заявив, что скорость падающего тела увеличивается пропорционально времени, прошедшему с момента начала падения объекта.

В 1590 году итальянский физик Галилео Галилей сформулировал закон, который установил определенную связь между расстоянием, пройденным падающим объектом, и временем. Он также доказал, что в отсутствие сопротивления воздуха все предметы на Земле падают с одинаковым ускорением, хотя до его открытия считалось, что тяжелые предметы падают быстрее.
Открыта новая величина — ускорение под действием силы тяжести и центробежное ускорение. Она выражается в виде g и применяется для разных мест на Земле, начиная от 9,78 м/с2 (значение на экваторе) до 9,83 м/с2 (значение на полюсах). На точность влияют долгота, широта, время суток и различные другие факторы.
Значение g по умолчанию принимается равным 9,80665 м/с 2. Для физических расчетов, не требующих высокой точности, значение ускорения принимается равным 9,81 м/с 2.
Чтобы показать, как падает объект в соответствии с открытием Галилея, ученые проводят следующий эксперимент: Они помещают предметы разного веса в длинную стеклянную трубку и вытягивают из нее воздух. Когда трубка перевернута вверх дном, все предметы падают на дно трубки одновременно под действием силы тяжести, независимо от их веса.
Когда одни и те же объекты помещены в среду, гравитация действует на них одновременно как сила сопротивления, поэтому объекты падают в разное время в зависимости от их массы, формы и плотности.
Формулы для расчетов
Существуют формулы, которые можно использовать для расчета различных величин, относящихся к
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с 2 ).
Не углубляясь в научные вопросы, повседневное определение свободного движения относится к движению тела в земной атмосфере, когда на него не влияет ничего, кроме сопротивления окружающего воздуха и силы тяжести.
Иногда добровольцы соревновались друг с другом в установлении личного рекорда. В 1962 году Евгений Андреев, парашютист-испытатель из СССР, установил рекорд, который был занесен в Книгу рекордов Гиннесса: В прыжке с парашютом в свободном падении он преодолел расстояние в 24500 метров, не используя парашют в качестве тормоза.
В 1960 году американцу Д. Киттингеру удалось совершить прыжок с парашютом с высоты 31 000 метров с тормозным устройством парашюта.
В 2005 году был установлен рекорд скорости свободного падения — 553 км/ч, а через семь лет был установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который всемирно известен своими опасными трюками.

Интересные факты
Давайте рассмотрим простой пример свободного падения. Предположим, что тело падает с высоты h с начальной скоростью, равной нулю. Предположим, мы поднимаем пианино на высоту h и оставляем его стоять.
Свободное падение — это прямолинейное движение с постоянным ускорением. Проведем координатную ось из точки начального положения тела на землю. Используя кинематические формулы для линейного равномерного ускорения, мы можем написать.
h = v 0 + g t 2 2 .
Поскольку начальная скорость равна нулю, мы переписываем ее:
Свободное падение тела
Таким образом, мы получаем выражение для времени падения тела с высоты h:
Поскольку v = g t, мы находим скорость тела в момент падения, т.е. максимальную скорость:
v = 2 h g — g = 2 h g .
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем мяч вверх.
Ось координат направлена вертикально вверх от точки бросания тела. В этот раз тело движется так же медленно и теряет скорость. В высшей точке скорость тела равна нулю. Используя формулы кинематики, мы можем написать:
Если мы подставим v = 0, то получим время, за которое тело достигнет максимальной высоты:
Время падения равно времени подъема, и тело возвращается на землю за время t = 2 v 0 g.
Движение тела, брошенного вертикально вверх
Максимальная высота подъема вертикально брошенного тела:
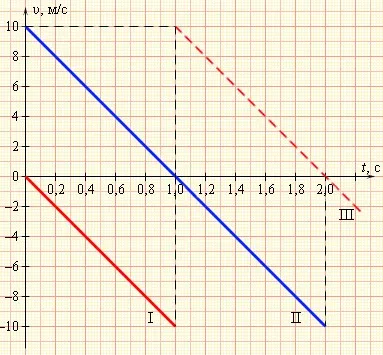
Давайте посмотрим на следующий рисунок. Здесь показаны графики скоростей тел для трех случаев движения с ускорением a = — g. Давайте рассмотрим каждый из этих случаев, предварительно указав, что в данном примере все числа округлены, а ускорение под действием силы тяжести принято равным 10 м с 2.
На первой диаграмме показано падение тела с определенной высоты без начальной скорости. Время падения t n = 1 с. Из формул и диаграммы легко вывести, что высота, с которой упало тело, равна h = 5 м.
На втором рисунке показано движение тела, брошенного вертикально вверх с начальной скоростью v 0 = 10 м с. Максимальная высота подъема h = 5 м. Время подъема и время падения t n = 1 с .
Третья диаграмма является продолжением первой. Падающее тело ударяется о поверхность, и его скорость резко меняет знак. Дальнейшее движение тела показано на второй диаграмме.
С проблемой свободного падения тела тесно связана проблема движения тела, брошенного под определенным углом к горизонту. Таким образом, движение по параболической траектории может быть представлено как сумма двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси O Y тело движется с эквивалентной скоростью с ускорением g, где начальная скорость этого движения равна v 0 y. Движение вдоль оси O X равномерное и прямолинейное, с начальной скоростью v 0 x .
Условиями для движения вдоль оси O X являются:
x 0 = 0 ; v 0 x = v 0 cos a ; a x = 0 .
Движение тела, брошенного под углом к горизонту
Условия для движения вдоль оси O Y :
y 0 = 0 ; v 0 y = v 0 sin α ; α y = — g .
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t = 2 v 0 sin α g .
Расстояние до тела:
L = v 0 2 sin 2 sin 2 a g .
Максимальный диапазон достигается при угле α = 45°.
L m a x = v 0 2 g .
Максимальная высота подъема:
h = v 0 2 sin 2 a 2 g .
Обратите внимание, что движение тела, брошенного под углом к горизонту, в реальных условиях может происходить не по параболической траектории из-за сопротивления воздуха и ветра. Особая наука, баллистика, изучает движение тел, брошенных в пространство.