Если к пружине подвесить груз, то получится пружина, которая колеблется в вертикальном направлении. Можно показать, что в этом случае формула (10) также применима к периоду колебаний.
Механические колебания.
ЕГЭ-Кодер Темы: гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебание — это изменение состояния системы, повторяющееся во времени. Понятие колебаний охватывает очень широкий спектр явлений.
Колебания механических систем или механические колебания — это механическое движение тела или системы тел, которое повторяется во времени и происходит вблизи положения равновесия. Положение равновесия — это состояние системы, в котором она может находиться в течение любого промежутка времени, не подвергаясь внешним воздействиям.
Например, когда маятник отклоняют и отпускают, он начинает раскачиваться. Положение равновесия — это положение маятника, когда он не отклоняется. Маятник может оставаться в таком положении сколь угодно долго, если не прикасаться к нему. Когда маятник качается, он проходит через положение равновесия много раз.
Сразу после освобождения отклоненного маятника он начинает двигаться, проходит через положение равновесия, достигает противоположного крайнего положения, останавливается там на мгновение, движется в обратном направлении, снова проходит через положение равновесия и возвращается обратно. Произошло полное колебание. Этот процесс повторяется через регулярные промежутки времени.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время полного колебания. Мы можем сказать, что за один период тело проходит расстояние в четыре ширины.
Частота колебаний равна обратной величине периода:. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний происходит за одну секунду.
Гармонические колебания.
Можно предположить, что положение вибрирующего объекта определяется одной координатой. Основная задача механики в этом случае — найти функцию, которая дает координаты тела в каждый момент времени.
Для математического описания колебаний, очевидно, следует использовать периодические функции. Существует множество таких функций, но две из них, синус и косинус, являются наиболее важными. Они обладают многими хорошими свойствами и тесно связаны с различными физическими явлениями.
Поскольку функции синуса и косинуса получаются друг из друга путем сдвига аргумента на, мы можем ограничиться одной из двух функций. Для безопасности мы будем использовать косинус.
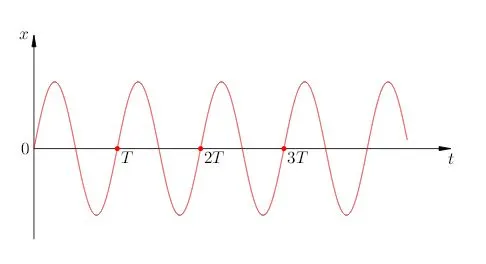
Гармонические колебания — это колебания, при которых координата e
Рисунок 1: Диаграмма гармонических колебаний
Гармонический закон вида (1) имеет наиболее общий характер. Это соответствует, например, ситуации, когда маятник одновременно подвергается двум начальным операциям: Он отклоняется на величину и получает начальную скорость. Есть два важных особых случая, когда одно из этих действий не выполняется.
Пусть маятник качается, но начальная скорость не задана (сработал без начальной скорости). Понятно, что в данном случае так можно выразиться. Получаем закон косинуса:
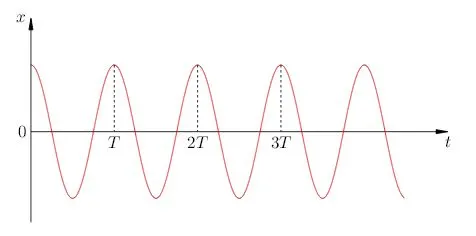
Диаграмма гармоник в этом случае показана на рисунке 2.
Рисунок 2. Закон косинуса показан на рисунке 2.
Теперь предположим, что маятник не отклоняется, а получает начальную скорость из положения равновесия в результате удара. В этом случае мы можем поставить. Получаем закон синусов:
Диаграмма колебаний показана на рис. 3 .
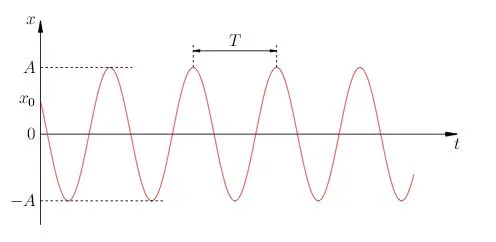 |
| Рисунок 3. Закон синуса. |
Вернемся к общему гармоническому закону (1). Мы хотим продифференцировать это уравнение:
Теперь продифференцируйте полученное равенство (4):
Сравним выражение (1) для координат и выражение (5) для проекции ускорения. Оказывается, что проекция ускорения отличается от координаты всего на один коэффициент:
 |
| Эта зависимость называется уравнением гармонических колебаний и может быть переписана в таком виде: |
С математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений являются функции (а не числа, как в обычной алгебре). Поэтому можно показать, что:
-Решением уравнения (7) является любая функция вида (1) с произвольным ,
 |
| -ни одна другая функция не является решением уравнения (1), которое может быть задано (1), -ни одна другая функция не является решением уравнения. |
Уравнение гармонических колебаний.
Другими словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только эти колебания. Две константы определяются начальными условиями — начальными значениями координаты и скорости.
Особенностью гармонических колебаний является их большое сходство. Каждое колебание маятника практически полностью повторяет предыдущее и последующее колебания.
Особенно это касается «скорости замаха». Если измерить время, которое требуется маятнику для раскачивания, то можно увидеть, что оно остается одинаковым для разных раскачиваний. Если взять много маятников разной длины, то получатся разные колебания, но время, в течение которого происходит каждое колебание, постоянно для каждого маятника.
Это время является наиболее важной характеристикой процесса осцилляции. Он называется периодом колебаний, обозначается латинской буквой $T$ и измеряется в секундах. Чем быстрее колебания (чем короче нить маятника), тем меньше время каждого колебания и тем короче период колебаний.
В колебательных процессах нередко в качестве характеристики «скорости» рассматривается не период одного колебания, а число колебаний в единицу времени. Эта величина называется частотой колебаний и обозначается греческой буквой $
u$ («ню»). Он равен отношению между количеством колебаний и временем, в течение которого они происходят:
Поскольку единицей времени в системе СИ является секунда, единицей частоты является «k
Из математики мы знаем, что делить на ноль нельзя. Это означает, что в формулу связи между периодом и частотой колебаний нельзя подставить период или ноль частоты — в обоих случаях такие колебания невозможны.
Период гармонических колебаний
Число оборотов в единицу времени, которое совершает тело при движении по круговой траектории, называется частотой вращения. Частота вращения обозначается греческой буквой n.
Если при катании на карусели в парке мы делаем один оборот за 20 секунд, то продолжительность оборота в этом случае составляет T = 20 секунд. Как мы можем определить частоту этого движения? Сколько оборотов делает карусель за 1 секунду?
Очевидно, что n = 1/T = 1/20 1 /с, т.е. за 1 с карусель совершает одну двадцатую часть полного оборота.

Частота гармонических колебаний
Таким образом, частота обращения является обратной величиной длительности обращения:
- N – число колебаний;
- t – время, за которое колебания произошли (сек).
Поэтому единицей измерения этой физической величины является обратная величина секунды, т.е. 1 /с или с-1 .

Связь периода и частоты колебаний
Чтобы определить меру скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту вращения. В действительности, тело совершает полный оборот за время, равное периоду вращения T. Тогда расстояние, которое проходит тело, равно длине окружности: l = 2πR :
или в соответствии с формулой (1):
Исходя из формул (2) и (3), центростремительное ускорение тела можно найти, выразив скорость через период или частоту вращения:
ЧАСТОТА
Мгновенную окружную скорость часто называют линейной скоростью.
Мера скорости тела на круговой траектории вычисляется по формуле:
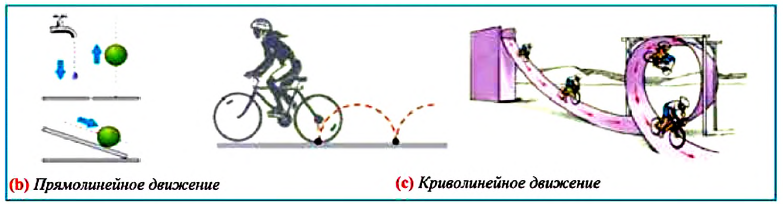
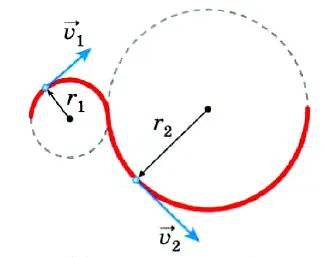
Способность описывать круговое движение объекта чрезвычайно важна, поскольку движение по криволинейной траектории можно аппроксимировать как движение по дугам окружности разного радиуса.
Найдем коэффициент скорости для вращения ребенка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, необходимое карусели для совершения полного оборота, равно 20 с.
Ответить
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
u = 0,722 м/с.
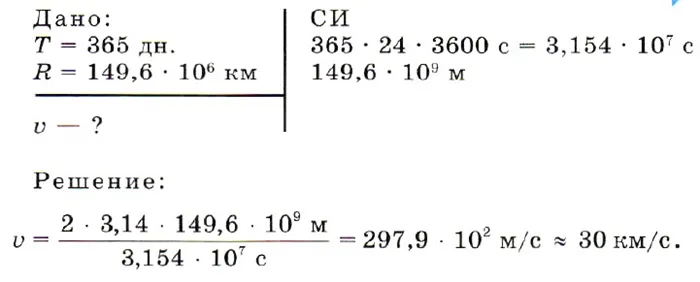
Задача 2: Земля совершает один оборот вокруг Солнца за 365 дней. Расстояние Солнца от Земли составляет 149,6 — 10 6 км. Давайте найдем линейную скорость движения Земли вокруг Солнца, рассматривая орбиту как круг.
Ответ
u ≈ 30 км/с.
Вы попали на урок физики 9: «Период и частота». …
РЕШЕНИЕ ЗАДАЧ