Скорость — это векторная величина, которая характеризуется не только своим коэффициентом, но и направлением. Если значение скорости положительное, то скорость направлена в положительном направлении оси x. Если значение скорости отрицательное, то скорость направлена в отрицательном направлении оси x.
Равномерное движение в физике — формулы и определение с примерами
В репортажах об автомобильных гонках или прогнозах погоды можно услышать, например: «Скорость победившего автомобиля перед финишной чертой составила 250 километров в час»; «Скорость ветра достигала 25 метров в секунду» и т.д. Что это значит? Как вы можете сравнить эти скорости?
Слово «скорость» известно вам уже давно. Поэтому, когда вы услышите, что скорость автомобиля составляет 20 метров в секунду, вы поймете: Автомобиль, движущийся с такой скоростью, преодолевает расстояние в 20 метров в секунду.
Представьте, какое расстояние этот автомобиль может преодолеть за 10 секунд, за полсекунды или за 0,1 секунды. Наверное, большинство из вас ответили именно так: За 10 секунд автомобиль проезжает 200 метров, за полсекунды — 10 метров, за 0,1 секунды — 2 метра. И эти ответы верны, если предположить, что автомобиль проезжает одинаковое расстояние за каждый (короткий или длинный) равный промежуток времени. То есть, если автомобиль движется равномерно.
Равномерное движение — это механическое движение, при котором тело проходит одинаковое расстояние за равные промежутки времени. Обратите внимание на слова «через равные промежутки времени». Иногда, даже учитывая неравномерность движения тела, можно определить такие равные промежутки времени, за которые тело проходит одинаковое расстояние. Например, пловец проплывает дорожку в бассейне (25 м) каждые 30 секунд, но мы не можем сказать, что он движется равномерно, потому что он замедляется при поворотах.
Равномерное прямолинейное движение
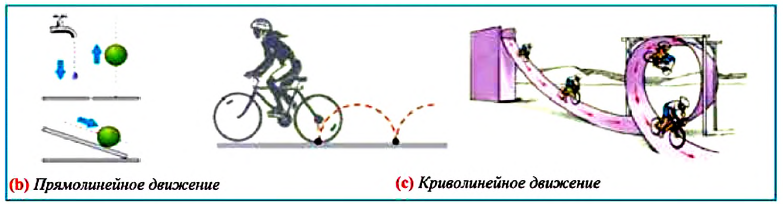
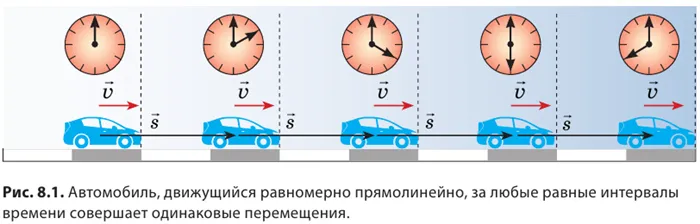
Если автомобиль движется равномерно на прямом участке дороги, то он движется равномерно (рис. 8.1), т.е. проходит одинаковое расстояние и не меняет направление движения. Такое движение называется равномерным прямолинейным движением.
Равномерное прямолинейное движение — это механическое движение, при котором тело движется равномерно через равные промежутки времени. Равномерное прямолинейное движение — это самый простой вид движения, который редко наблюдается в жизни. Примерами такого движения являются движение автомобиля по прямой трассе (без ускорения и торможения), падение металлического шарика в растительном масле, полет парашютиста через несколько часов после раскрытия парашюта.
Определение скорости равномерного движения
Мы полагаем, что вам не составит труда определить скорость равномерного движения, например, скорость пешехода, преодолевающего 30 метров за 20 секунд. Вы знаете из ма
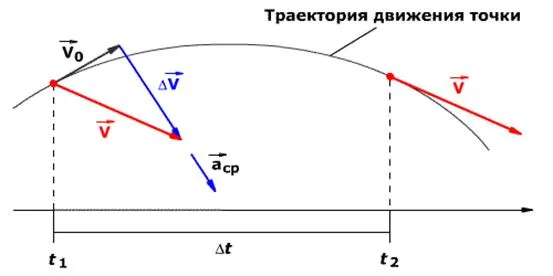
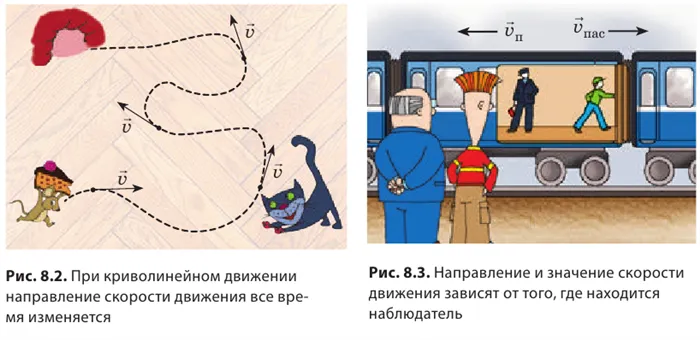
Если тело движется равномерно вдоль прямой линии, то величина и направление скорости остаются постоянными (см. рис. 8.1). Если тело движется равномерно по криволинейной траектории, то значение скорости остается неизменным, но направление постоянно меняется (рис. 8.2). Направление и величина скорости зависят от тела, по отношению к которому рассматривается движение. Представьте, что вы сидите в вагоне поезда, идущего на восток (рис. 8.3), и поезд движется через станцию со скоростью, противоположной направлению движения поезда. Считаете ли вы, что скорость пассажира одинакова для вас и для людей, стоящих на платформе? Нет, конечно, нет! Для вас пассажир движется со скоростью
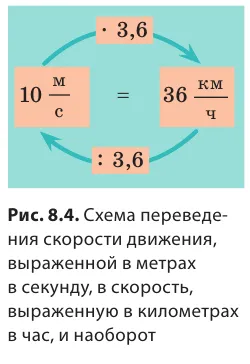
Значение скорости может быть выражено в единицах, отличных от метров в секунду. Например, автомобиль движется со скоростью 36 километров в час, а улитка ползет со скоростью 18 сантиметров в минуту. Попробуйте выразить скорости ракеты и улитки (см. выше) в метрах в секунду. Сложнее перевести скорость, указанную в метрах в секунду, в другие единицы, но порядок действий остается тем же. Например, скорость аэроплана составляет 250 м/с. Представим его в километрах в час, помня, что 1 метр = 0,001 км,
Скорость движения
Чтобы выразить скорость в метрах в секунду в километрах в час (и наоборот), мы можем использовать диаграмму, показанную на рисунке 8.4.
1. равномерное прямолинейное движение — это движение, при котором тело совершает одинаковые движения через одинаковые промежутки времени. Слова «одинаково» означают, что тело движется одинаково каждый час, каждую минуту, каждые 30 минут, каждую секунду и каждую долю секунды.
Равномерное движение — это идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно длительного периода времени. Реальное движение может приближаться к равномерному движению только с определенной степенью точности. 2.
2. изменение положения тела в пространстве при равномерном движении может происходить с разными скоростями. Это свойство движения, его «скорость», характеризуется физической величиной, называемой скоростью.
Равномерное прямолинейное движение
Скорость равномерного линейного движения — это векторная физическая величина, которая соответствует отношению между перемещением и временем, за которое произошло перемещение.
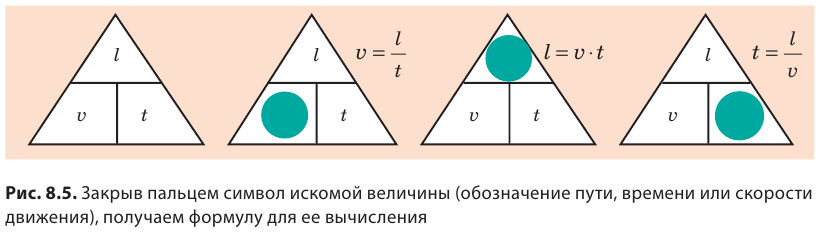
Если тело переместилось за время \( t \) \( \vec \), то его скорость равна \( \vec=\frac
единица скорости: \( \,v\,=\frac\)? \( \,v,=\frac=1\frac \). Единицей скорости является 1 м/с, скорость g
Пусть \( \vec \) будет смещением тела (Рисунок 11). Совместим координатную ось OX в направлении смещения. Найдите проекцию смещения на координатную ось OX. На рисунке \( x_0 \) — координата начальной точки перемещения, \( x \) — координата конечной точки перемещения. Проекция перемещения равна разности между координатами начальной и конечной точек: \( \vec_x=x-x_0 \). С другой стороны, проекция смещения равна проекции скорости на время, т.е. \ С другой стороны, разница между скоростью и скоростью, умноженной на время, равна времени движения. Поэтому \( x-x_0=\vec_xt \) или \( x=x_0+\vec_xt \). Если начальная координата \( x_0 \) = 0, то \( x=\vec_xt \) .
Эта формула может быть использована для определения координаты тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.<\vec>\) .
x_0 \). Проекция скорости отрицательна, если тело движется в положительном направлении оси OX (рис. 12). В этом случае \( x
Зависимость координаты от времени можно показать графически.
Предположим, что тело движется с постоянной скоростью из начала координат в положительном направлении оси OX. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае выглядит следующим образом: \( x \) = 4 м/с — \( t \). Зависимость координаты от времени линейная. Эта зависимость представлена в виде прямой линии, проходящей через начало координат (рис. 13).
1. какова проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с 2) 80 м/с 3) 20 м/с 4) 0,05 м/с
Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае \( x>2) Какова мера перемещения мухи за 0,5 минуты, если она летит со скоростью 5 м/с?

1) 0,25 м 2) 6 м 3) 10 м 4) 150 м
Автомобиль Renault преодолевает расстояние в 1,2 км за 1 минуту. Peugeot преодолевает расстояние в 0,2 км за 20 секунд. Сравните скорость Renault \( v_1 \) и скорость Peugeot \( v_2 \).
ПРИМЕРЫ ЗАДАНИЙ
1) \( v_1=v_2 \) 2) \( v_1=2v_2 \) 3) \( 2v_1=v_2 \) 4) \( 1,2v_1=10v_2 \)
На рисунке изображена гистограмма. Она представляет собой расстояние, пройденное мухой (1) и воробьем (2) за одно и то же время, когда они движутся с одинаковой скоростью. Сравните их скорости \( v_1 \) и \( v_2 \).
1) \( v_1=v_2 \) 2) \( v_1=2v_2 \) 3) \( 3v_1=v_2 \) 4) \(2v_1=v_2)
На рисунке представлен график зависимости коэффициента скорости равномерного движения от времени. Мера перемещения тела за 2 с равна
1) 20 м 2) 40 м 3) 80 м 4) 160 м
Диаграмма на рисунке показывает расстояние, пройденное телом при равномерном движении, как функцию времени. Мера скорости тела равна
1) 0,1 м/с 2) 10 м/с 3) 20 м/с 4) 40 м/с.

На рисунке представлены графики зависимости расстояния от времени для трех тел. Сравните скорости \( v_1 \), \( v_2 \) и \( v_3 \) этих тел.
v_3 \) 3) \( v_1 4) \( v_1=v_2 \), \( v_3

8. какая из следующих диаграмм отражает связь между расстоянием и временем при равномерном движении тела?
9. на следующем рисунке изображена диаграмма координат тела как функция времени. Какова координата тела в момент времени 6 с?

1) 9,8 м

1) \( v_1=v_2=v_3 \) 2) \( v_1>v_2>