Формула магнитного потока. В чем измеряется магнитный поток?

Поток является скалярной величиной, и его единицей измерения является Вебер (Vb): 1 Vb = 1 T * m 2, т.е. F = T * m 2 .

Магнитный поток простыми словами

Вероятно, термин «поток» ассоциируется у вас с течением воды. Если бы вы хотели описать этот поток количественно, вы бы имели в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Этот поток может переносить большое или малое количество воды, в зависимости от скорости движения воды и поверхности этого сечения.

Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная, довольно абстрактная величина. Но, как вы правильно догадались, название берет свое начало в гидродинамике. Здесь, однако, нет потока вещества через поверхность, а есть только векторы магнитной индукции B, которые «пронизывают» поверхность и иногда «скользят» по ней.

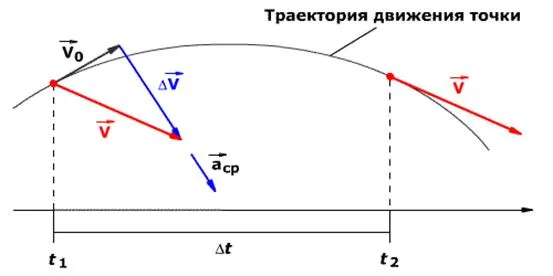
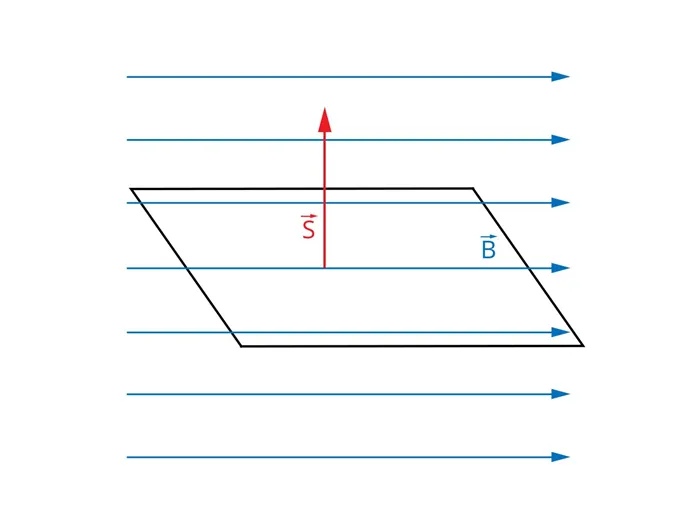
Представим себе однородное магнитное поле, описываемое вектором магнитной индукции B. Плоскую поверхность с полем S мы помещаем в это поле произвольным образом, то есть под произвольным углом к вектору B (рис. 1). Теперь определим вектор B, который перпендикулярен плоскости поверхности. Длина этого вектора равна размеру поверхности.

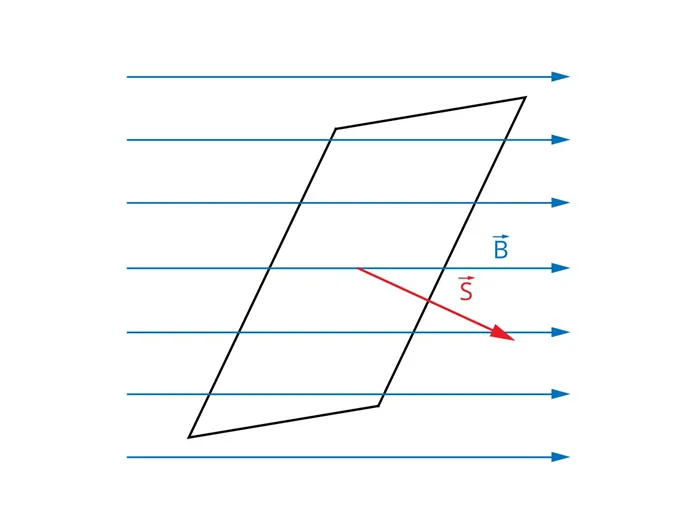
Поток вектора магнитной индукции F_Bчерез поверхность S является скалярным произведением векторов B и S .

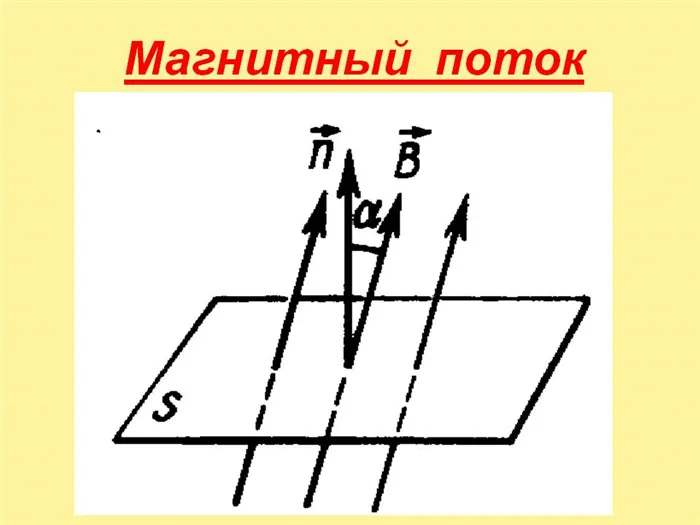
Поэтому мы можем определить термин «магнитный поток» следующим образом:

Магнитный поток — это поток вектора магнитной индукции B через поверхность. Для бесконечно малой поверхности она равна произведению коэффициента | B | поверхности dS и косинуса угла a между B и перпендикуляром n к плоскости поверхности. Для конечно-мерной поверхности это сумма (интеграл) по ее малым частям.

Википедия

Зависимости магнитного потока

Из формулы видно, что магнитный поток зависит от трех переменных: магнитного поля B, поверхности S и угла α.

Магнитный поток линейно зависит от B и S. Например, если увеличить поверхность S, но оставить магнитное поле B и угол α прежними, магнитный поток будет больше. Поэтому большая площадь поверхности означает большой магнитный поток, а малая площадь поверхности — малый магнитный поток.

Если, с другой стороны, магнитное поле B увеличивается, магнитный поток также увеличивается. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.

В общем случае, чем больше магнитное поле B или площадь S, тем больше магнитный поток.

Ситуация с углом a немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда угол α = 0°. Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. При α = 90° магнитный поток равен нулю, так как магнитное поле параллельно магнитному полю.

Примеры

Как вычислить поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую нужно рассчитать поток, на такие маленькие участки, что можно считать их плоскими, а поле — однородным. Все это делается для того, чтобы мы могли применить определение потока. Поэтому мы рассчитываем небольшие «потоки» и складываем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:

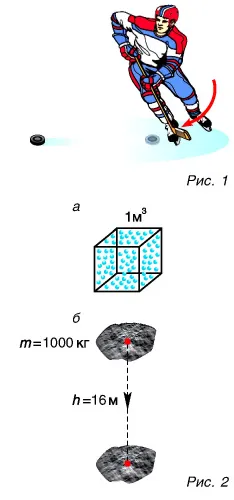
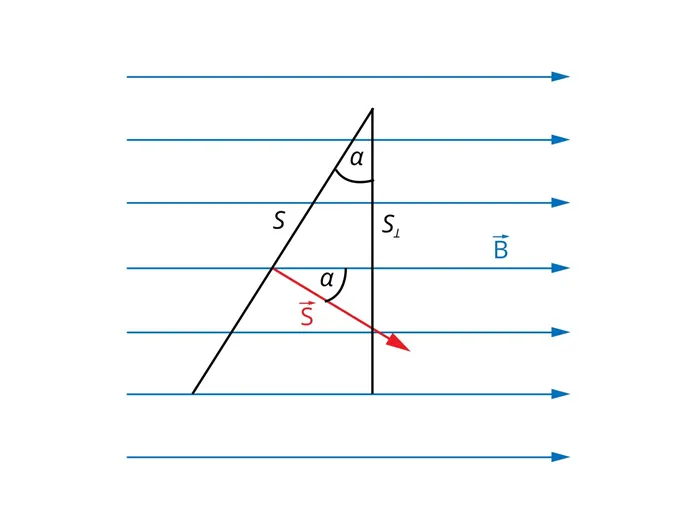
1. В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: Ф_B= B * S и при этом его значение максимально, так как:

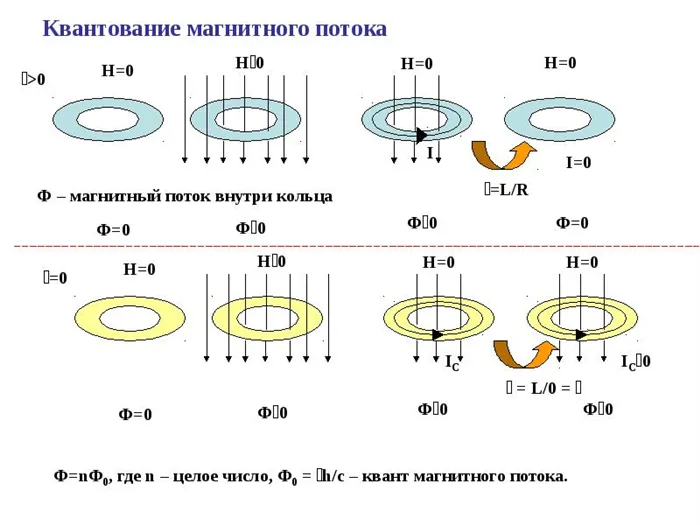
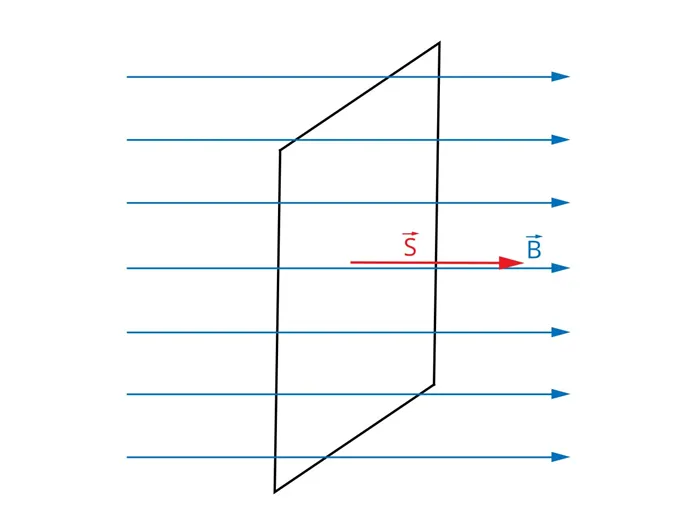
Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры._BПроводя эксперименты и работая в области магнитных явлений, Вебер дал определение магнитному потоку. Он описал его как меру силы и расширения МП. Это одна из физических величин, которую можно определить, зная коэффициент вектора магнитной индукции B→ (ВМИ). Нам также нужно знать площадь пересечения и синус угла между VMI и перпендикуляром к плоскости.

Магнитный поток обозначается буквой F и измеряется в веберах (Vb). Аппарат назван по фамилии ученого. Таким образом, 1 Вб обозначает магнитный поток Ф, создаваемый магнитным полем с индукцией в один тесла (1 Тесла), пересекающим площадь в один квадратный метр (1 м²), при условии, что эта площадь перпендикулярна ВМИ (В→).

Магнитные потоки, которые можно определить с помощью специальных приборов, называемых флюксметрами, измеряются как в лаборатории, так и в полевых условиях. Эти приборы также называются флюксметрами. Особенностью этих счетчиков с магнитоэлектрической системой (MES) является то, что ток подается на подвижную рамку без рамки через катушки, не имеющие противодействующего (безмоментного) вращающего момента.

Предупреждение. В момент отсутствия тока индикатор не имеет фиксированного положения на шкале.

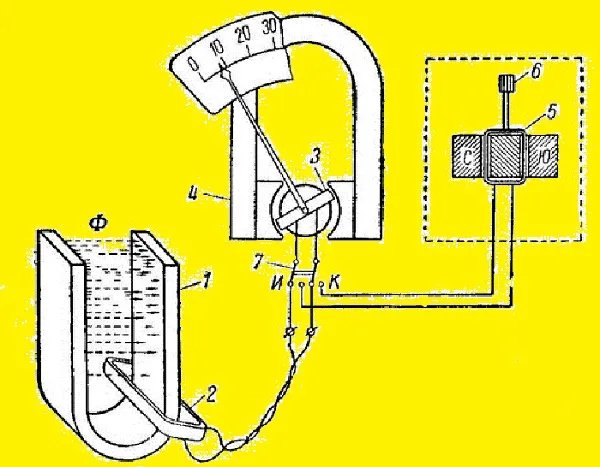
Устройство состоит из следующих частей, обозначенных на рисунке выше:_BРасходомер не может измерять слабые МП из-за низкой чувствительности._⟂Великий немецкий ученый Карл Гаусс, преуспевший в математике, физике и астрономии, установил закон (теорему) в области магнетизма. Он доказал, что в отличие от электрического поля, которое генерируется электрическими зарядами, МП не генерируется магнитными зарядами. В классической электродинамике их просто не существует._⟂Информация. Теорема, выведенная Гауссом, является одним из важнейших законов электродинамики и входит в систему уравнений Максвелла. Она описывает связь между потоком напряженности электрического поля через замкнутую произвольную поверхность и суммой зарядов, расположенных в объеме, описываемом поверхностью. Сумма выражается в алгебраической форме.

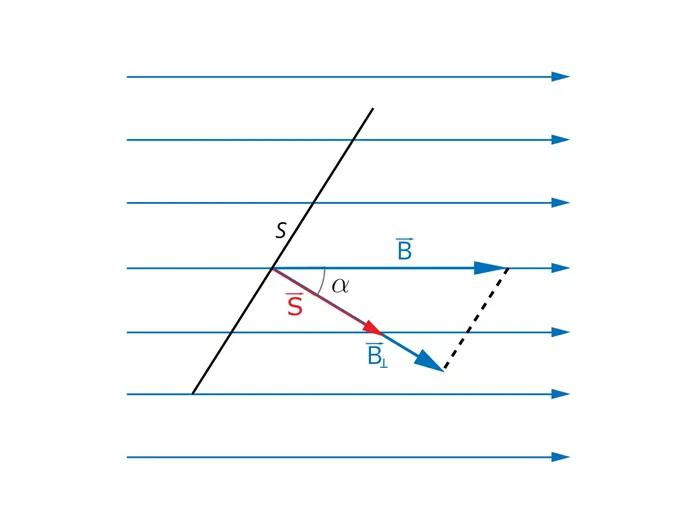
Что касается магнитной индукции, то поток B→, протекающий через замкнутую поверхность S, имеет значение ноль

Поток вектора магнитной индукции может быть отрицательным или положительным. Это связано с выбором положительного направления. Очень часто поток вектора магнитной индукции связан с контуром, по которому протекает ток. В этом случае положительное направление перпендикуляра к цепи связано с направлением тока, протекающего через правосторонний боррель. Тогда магнитный поток, создаваемый контуром тока через область, ограниченную этим контуром, всегда больше нуля.

Что такое магнитный поток

Единицей потока магнитной индукции в Международной системе единиц (СИ) является Вебер (Вб). Формула (4) может быть использована для определения единицы магнитного потока. Вебер — это магнитный поток, проходящий через плоскую поверхность площадью 1 квадратный метр перпендикулярно потенциальным линиям однородного магнитного поля:

Единицы измерения

Теорема Гаусса для потока магнитного поля отражает тот факт, что магнитных зарядов не существует, поэтому линии магнитной индукции всегда замкнуты или простираются до бесконечности, у них нет начала и конца.

Измерительные приборы

Теорема Гаусса для магнитного потока формулируется следующим образом: Магнитный поток через замкнутую поверхность (S) равен нулю. Математически эта теорема может быть описана следующим образом:

Оказывается, что теорема Гаусса для потоков вектора магнитной индукции ( ) и напряженности электростатического поля ( ) через замкнутую поверхность принципиально различны.

Задание

• испытуемый постоянный магнит – 1;
• рамка измерительная – 2;
• рамка прибора – 3;
• магнит прибора – 4;
• рамка корректирующего устройства – 5;
• головка регулировки корректирующей рамки – 6;
• переключатель «работа – коррекция» – 7.

Вычислите поток вектора магнитной индукции через катушку соленоида с N витками, длиной сердечника l, площадью поперечного сечения S, магнитной проницаемостью сердечника. Сила тока, протекающего через магнит, равна I.

Теорема Гаусса для магнитной индукции

Решение

Поэтому магнитный поток через одну катушку соленоида равен ( ):

Общий поток магнитной индукции, проходящий через все катушки:

Поток магнитной индукции

Где x — расстояние между проводником и точкой, в которой рассматривается поле. Для определения необходимого магнитного потока мы используем следующую формулу:

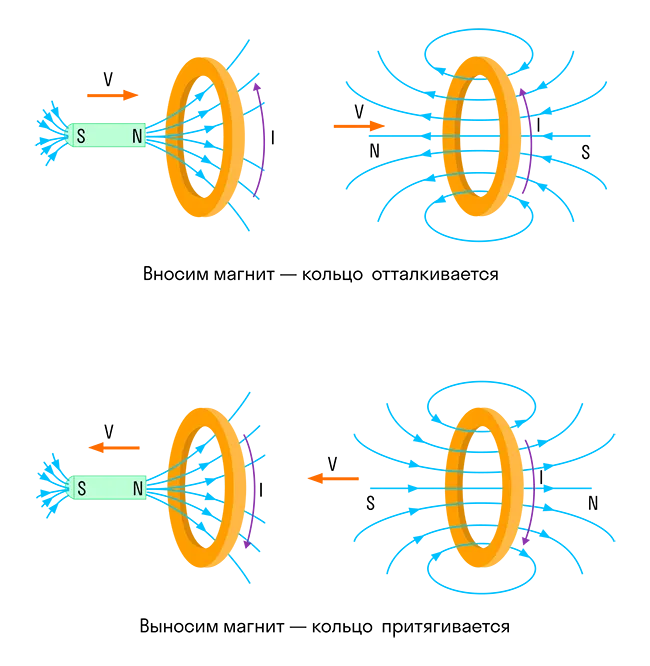
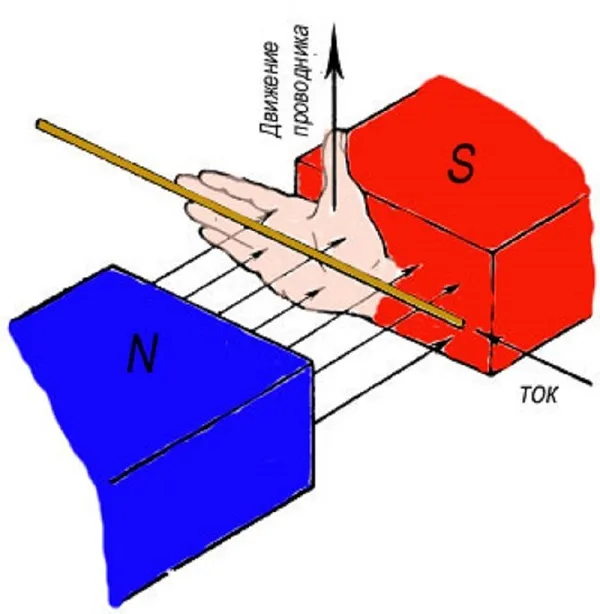
Правило Ленца