3 — сердечник, в верхней части которого имеется прорезь для маленькой отвертки. Вкручивание или выкручивание сердечника изменяет индуктивность катушки.
Катушка индуктивности
Что вы имеете в виду под «катушкой»? Ну… возможно, это какая-то «штука» с веревкой, леской, канатом, чем угодно! Индуктор — это точно такое же устройство, но вместо нити, струны или чего-то еще, вы наматываете на него обычный изолированный медный провод.
В качестве изоляции может использоваться бесцветный лак, изоляция из ПВХ или даже ткань. Хитрость заключается в том, что хотя провода в катушке находятся очень близко друг к другу, они все равно изолированы друг от друга. Если вы наматываете катушку своими руками, никогда не используйте обычную голую медную проволоку!
Индуктивность
Каждая катушка индуктивности имеет индуктивность. Индуктивность катушки измеряется в Генри (Гн), обозначается буквой L и измеряется с помощью LC-метра.
Что такое индуктивность? Когда электрический ток течет по проводу, он создает вокруг него магнитное поле:
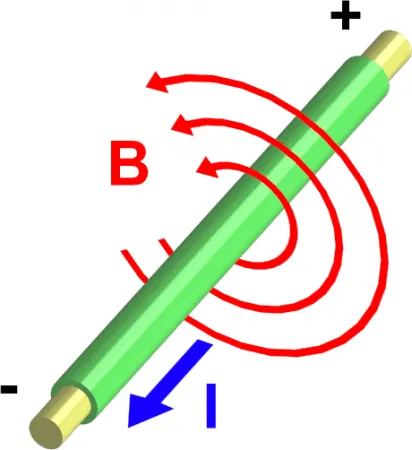
B — магнитное поле, Vb — магнитное поле.
Итак, давайте возьмем этот провод, намотаем его и подадим напряжение на его концы.

И у вас есть изображение магнитных силовых линий:

Грубо говоря, чем больше линий магнитного поля пересекает поверхность соленоида, в нашем случае поверхность катушки, тем больше магнитный поток (Ф). Поскольку катушка возбуждается электрическим током, это означает, что катушка возбуждается током силы (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и рассчитывается по формуле:
В научных терминах индуктивность — это способность забирать энергию от источника электрического тока и сохранять ее в виде магнитного поля. Когда ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а когда ток уменьшается, магнитное поле сжимается.
Самоиндукция
Индукционная катушка также обладает очень интересным свойством. Когда к катушке прикладывается постоянное напряжение, в течение короткого времени на ней возникает обратное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭЭД зависит от величины индуктивности катушки. Таким образом, при подаче напряжения на катушку ток равномерно изменяется от нуля до определенного значения в течение доли секунды, поскольку напряжение также изменяется от нуля до постоянного значения при подаче тока. Согласно закону Ома:
I — ток в катушке, A
U — напряжение на катушке, V
R — сопротивление катушки, Ом
Как видно из формулы, напряжение изменяется от нуля до напряжения, приложенного к катушке, поэтому ток также изменяется от нуля до определенного значения. Сопротивление катушки постоянному току также постоянно.
Второй эффект при использовании индукционной катушки заключается в том, что при размыкании цепи между катушкой и источником к уже приложенному к катушке напряжению добавляется ЭДС, которая сама себя контролирует.
Это означает, что когда мы размыкаем цепь, напряжение на катушке в этот момент может быть во много раз выше, чем до размыкания цепи, а ток в цепи катушки будет спокойно падать, так как самореагирующий ЭЭД поддерживает падающее напряжение.
Давайте сделаем первые выводы о том, как работает индукционная катушка при подаче на нее постоянного тока. При подаче электрического тока на катушку сила тока равномерно увеличивается, а при снятии электрического тока с катушки сила тока равномерно уменьшается до нуля. Короче говоря, ток в катушке не может измениться мгновенно.
Явление самоиндукции
Когда ток, протекающий по проводящей цепи, изменяется по величине, возникает явление самоиндукции. В этом случае магнитный поток через контур изменяется, и в проводниках токоведущей рамки возникает ВЭД, так называемая автоиндукционная ВЭД. Эта ЭДС противоположна направлению тока и равна:
Очевидно, что ЭДС самоиндукции равна скорости изменения магнитного потока, вызванного изменением тока, протекающего через контур, и также пропорциональна скорости изменения тока. Коэффициент пропорциональности между самоиндукцией EED и скоростью изменения тока называется индуктивностью и обозначается L. Эта величина всегда положительна, а единицей СИ является 1 Генри (1 Гн). Используются также дроби от этого — миллигенералы и микрогенералы. Об индуктивности в 1 Генри можно говорить, когда изменение тока в 1 ампер вызывает ЭДС самоиндукции в 1 вольт. Индуктивностью обладает не только контур, но и простой проводник, и катушка, которую можно представить как несколько последовательно соединенных контуров.
Энергия накапливается в индуктивности, которую можно рассчитать следующим образом: W=L*I 2 /2, где:
- W – энергия, Дж;
- L – индуктивность, Гн;
- I – ток в катушке, А.
Здесь энергия прямо пропорциональна индуктивности катушки.
Важно: В механике индуктивность также является устройством, в котором сохраняется электрическое поле. Элементом, который ближе всего подходит к этому определению, является индукционная катушка.
Общая формула для расчета индуктивности физической катушки имеет сложный вид и не подходит для практических расчетов. Полезно помнить, что индуктивность пропорциональна числу витков и диаметру катушки и зависит от геометрической формы. На индуктивность также влияет магнитная проницаемость сердечника, в котором находится катушка, но не ток, протекающий через катушки. Для расчета индуктивности в каждом конкретном случае необходимо использовать формулы, приведенные для конкретной конструкции. Для цилиндрической катушки, например, основная характеристика рассчитывается по следующей формуле:
Читайте также.
- μ – относительная магнитная проницаемость сердечника катушки;
- μ – магнитная постоянная, 1,26*10-6 Гн/м;
- N – количество витков;
- S – площадь витка;
- l – геометрическая длина катушки.
Для расчета индуктивности для цилиндрической катушки и катушек других форм лучше всего использовать калькуляторы, в том числе онлайн-калькуляторы.
Последовательное и параллельное соединение индуктивностей
Индукторы могут быть соединены последовательно или параллельно, в результате чего получается серия с новыми свойствами.
Параллельное соединение
Когда катушки соединены параллельно, напряжения на всех элементах равны, а токи (переменные) распределяются обратно пропорционально индуктивностям элементов.
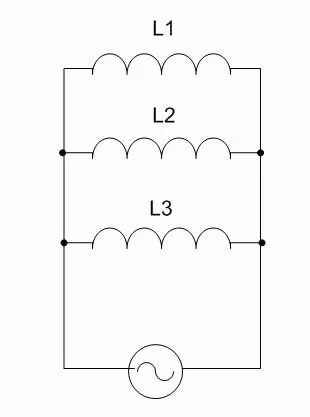
Общая индуктивность цепи определяется как 1/L=1/L1+1/L2+1/L3. Формула применима к любому количеству элементов и упрощается до L=L для двух катушек.1*L2/(L1+L2Очевидно, что результирующая индуктивность меньше, чем индуктивность элемента с наименьшим значением
Последовательное соединение
При таком типе подключения через цепь, состоящую из катушек, протекает один и тот же ток, а напряжение (переменное напряжение!) на каждом элементе цепи распределяется в соответствии с индуктивностью каждого элемента:
Общая индуктивность равна сумме всех индуктивностей и больше индуктивности элемента с наибольшим значением. Поэтому это соединение используется, когда требуется увеличение индуктивности.

Это важно: если катушки соединены последовательно или параллельно, расчетные формулы применимы только в том случае, если исключена взаимная интерференция магнитных полей элементов друг с другом (в случае экранирования, больших расстояний и т.д.). При наличии помех общее значение индуктивности зависит от взаимного расположения катушек.
Некоторые практические вопросы и конструкции катушек индуктивности
На практике используются различные конструкции индукционных катушек. В зависимости от назначения и применения устройства могут быть сконструированы по-разному, с учетом эффектов, возникающих в реальных катушках.
Добротность катушки индуктивности
Реальная катушка имеет много других параметров, кроме индуктивности, из которых коэффициент качества является одним из самых важных. Эта величина определяет потери в катушке и зависит от них:
- омических потерь в проводе обмотки (чем больше сопротивление, тем ниже добротность);
- диэлектрических потерь в изоляции провода и каркасе обмотки;
- потерь в экране;
- потерь в сердечнике.
Все эти величины определяют сопротивление потерь, а коэффициент качества — это безразмерная величина, соответствующая Q=ωL/R потерь, где:
- ω = 2*π*F – круговая частота;
- L – индуктивность;
- ωL – реактивное сопротивление катушки.
Читайте также:Определение направления магнитной индукции с помощью правила Бора и правила правой руки.
В качестве грубого приближения можно сказать, что коэффициент качества равен отношению между реактивным (индуктивным) сопротивлением и активным сопротивлением. С одной стороны, числитель увеличивается с ростом частоты, с другой стороны, из-за скин-эффекта сопротивление потерь также увеличивается, так как эффективное сечение провода уменьшается.
Экранный эффект
Для уменьшения влияния инородных тел, а также электрических и магнитных полей и взаимного влияния элементов этими полями, катушки (особенно высокочастотные) часто экранируют. Помимо положительного эффекта, экранирование вызывает снижение добротности катушки, уменьшение индуктивности и увеличение паразитной емкости. Более того, чем ближе стенки экранирующей оболочки расположены к виткам катушки, тем больше отрицательный эффект. Поэтому экранированные катушки почти всегда проектируются регулируемыми.
Подстроечная индуктивность
В некоторых случаях для компенсации резонансных отклонений необходимо точно отрегулировать значение индуктивности на месте после подключения катушки к другим элементам схемы. Для этого существуют различные методы (переключение витков и т.д.), но самым точным и плавным методом является резонанс сердечника. Для этого используется резьбовой стержень, который можно вращать в каркасе для регулировки индуктивности катушки.

Переменная индуктивность (вариометр)
Когда требуется функциональная регулировка индуктивности или индуктивной связи, используются катушки различных конструкций. Они содержат две обмотки, звуковую и неподвижную катушки. Общая индуктивность равна сумме индуктивностей двух катушек и взаимной индуктивности между ними.
Изменяя относительное положение одной катушки относительно другой, регулируется общее значение индуктивности. Такое устройство называется весоизмерительным прибором и имеет

Единица измерения индуктивности
Обратите внимание, что определение не является строгим, но оно позволяет нам определить единицу измерения индуктивности. Значение $L$ зависит от геометрических свойств проводника (форма, размеры) и относительной магнитной проницаемости среды, в которой находится проводник. Иногда проводят аналогию между индукцией и массой тела. В этом случае говорят, что масса тела не позволяет ему мгновенно изменить свою скорость (или кинетическую энергию), так же как индукция не позволяет магнитному полю мгновенно изменить свою энергию. Выражение для кинетической энергии тела в виде:
Формула для энергии магнитного поля:
В Международной системе единиц (СИ) генри — это единица индукции. Аббревиатура — Gn. Цепь имеет индуктивность 1 Гн, если изменение тока со скоростью 1 ампер в секунду вызывает электродвижущую силу (ЭДС) 1 вольт.
Генри — производная единица в системе СИ. Выразим Генри (Hn) в базовых единицах СИ. Для этого используется выражение (2).
Генри — единица измерения индуктивности, названная в честь американского ученого Дж. Генри. Он был введен в систему СИ в 1960 году. При использовании этой единицы измерения в системе СИ префиксы стандартной системы могут использоваться для образования десятичных кратных и долей. Например: kGn (килогенри) — nGn (наногенри):
В гауссовой системе единиц и системе GHSM (это варианты системы GHS) сантиметр является единицей индукции. Отношение индукции в этих системах к генри определяет экспрессию:
Единицы измерения индуктивности в СГС и связанных с ней систем
Чтобы избежать путаницы с сантиметром как единицей индукции, иногда используется термин абгенерия.
В системе GHSE (расширение системы GHS) единица индукции считается безразмерной или обозначается как statgeneri:
\1статгенерация\ca. 8.987552\cdot ^Gn.\
Примеры задач с решением
Решение. В качестве основы для решения задачи возьмем выражение:
Из этого следует, что:
Воспользуемся выражением (1.2), чтобы получить единицу $L$, выраженную в базовых единицах СИ:
Где $\leftE_I
ight=J=H\cdot m;;\leftI
ight=A.$
Реакция. Из данного выражения следует, что единица индукции Генри выражается в базовых единицах СИ так: $Gn=\frac.$<>
Задание. Какова индуктивность катушки в резонансном контуре, если для емкости конденсатора $C=50пФ$ частота свободных колебаний составляет $
u=10МГц$? Проверьте формулу. В каких единицах измеряется результирующая индуктивность?
Решение. Давайте сделаем рисунок.
В данном колебательном контуре нет сопротивления, а частота колебаний зависит от номинала
Соленоид — это длинная тонкая катушка, т.е. катушка, длина которой намного больше ее диаметра (опять же, в дальнейших расчетах предполагается, что толщина обмотки намного меньше диаметра катушки). В этих условиях и без магнитного материала плотность магнитного потока составляет

Это дает формулу для индуктивности катушки соленоида (без сердечника):
Индуктивность соленоида


Для однослойного (очень тонко намотанного), конечного по размеру (не бесконечно длинного) соленоида существуют более точные, хотя и более сложные формулы 18 :
\leftВ случае, когда 1″ width=»» height=»» />\left( C\left( \sqrt
Более точные формулы для соленоида конечного размера
>ight) -\links( 1-m<-8w + 4\frac>ight) E\links( \sqrt<\frac>\left<\frac>\right) \right) \right\>» width=»» height=»» />
+\sum_^<1-\frac<3\pi>\Frac<\infty>— Радиус цилиндра,, — Эллиптические интегралы.<\left( 2n\right)!^2>>\left( -1\right) ^w^\right\>,» width=»» height=»» />
для
-
\left( 1 — \frac
Для тороидальной катушки, заключенной в сердечник из высокопроницаемого материала, можно приближенно использовать формулу для бесконечной прямой трубы (см. выше):<3\pi>+ \frac — \frac + \frac — \frac +. \right), » width=»» height=»» />
- для 1:» width=»» height=»» />
+ O(\frac) \right) \ln — 1/2 + \frac + O(\frac) \right\>. » width=»» height=»» />
Индуктивность тороидальной катушки (катушки с кольцевым сердечником)


где — большой радиус кольца).
,\, » width=»» height=»» />
Более точное приближение дает формула
Это предполагает, что сердечник имеет прямоугольное сечение с внешним радиусом R и внутренним радиусом r, и высотой h.
\cdot \ln \frac,\, » width=»» height=»» />
Для длинного прямого (или квазилинейного) провода с круглым сечением индуктивность выражается приближенной формулой 19:
Индуктивность длинного прямого проводника
где — относительная магнитная проницаемость внешней среды (которой заполнено пространство), относительная магнитная проницаемость материала проводника, — радиус его поперечного сечения.
l \Big( \mu_e \mathrm\frac + \frac\mu_i \Big), » width=»» height=»» />