Если скорости тел до и после столкновения направлены вдоль горизонтальной оси, то закон сохранения импульса должен быть записан в проекциях на ось ОХ. Не следует забывать, что знак проекции вектора:
Импульс
Темы в кодификаторе ЕГЭ: импульс тела, импульс системы тел, сохранение импульса.
Импульс тела — это векторная величина, равная произведению массы тела и его скорости:
Для импульса не существует конкретных единиц измерения. Для импульса не существует особых правил. Размерность импульса — это просто произведение размерности массы на размерность скорости:
Почему концепция импульса интересна? Оказывается, с его помощью можно перевести второй закон Ньютона в несколько иную форму, которая также чрезвычайно полезна.
Второй закон Ньютона в импульсной форме
Be — чистый результат действия сил, действующих на тело массы. Начнем с обычных обозначений второго закона Ньютона:
Поскольку ускорение тела равно производной от вектора скорости, второй закон Ньютона формулируется следующим образом:
Поставьте константу под знак производной:
Как мы видим, левая часть содержит производную от импульса:
Аналогия ( 1 ) — это новая форма формулировки второго закона Ньютона.
Второй закон Ньютона в форме импульса. Производная импульса тела является чистым результатом действия сил, действующих на тело.
Можно также сказать, что составляющая силы, действующей на тело, равна скорости изменения импульса тела.
Производная в формуле ( 1 ) может быть заменена отношением конечных приращений:
В данном случае это средняя сила, действующая на тело в течение определенного периода времени. Чем меньше значение, тем ближе отношение к производной, и тем ближе средняя сила к ее мгновенному значению в данный момент времени.
В случае проблем этот период времени обычно довольно короткий. Это может быть, например, момент удара мяча о стену, а затем средняя сила, действующая на мяч со стороны стены в момент удара.
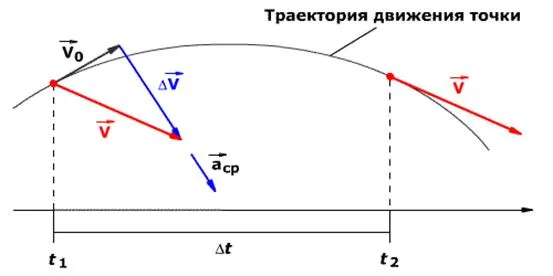
Вектор в левой части уравнения ( 2 ) — это изменение импульса во времени. Изменение импульса — это разница между конечным и начальным векторами импульса. То есть, если — импульс тела в определенный начальный момент времени, — импульс тела через промежуток времени, то изменение импульса — это разность:
Мы хотели бы еще раз подчеркнуть, что изменение импульса — это разность векторов (рис. 1):
 |
| Рис. 1. изменение импульса (см. рис. 1). |
Предположим, что мяч летит перпендикулярно стене (импульс до удара равен ) и отскакивает без потери скорости (импульс после удара равен ). Хотя импульс по модулю ( ) не изменился, происходит изменение импульса:
Геометрически эта ситуация показана на рисунке 2:
 |
| Рисунок 2. Изменение импульса при ударе. |
Мера изменения импульса, как видно, равна удвоенной мере начального импульса сферы: .
Формула ( 2 ) может быть переписана следующим образом:
Или запишите изменение импульса, как указано выше:
Эта величина называется импульсом силы. Для импульса силы не существует специальной единицы измерения; размерность импульса силы — это просто произведение размерности силы и времени:
(Обратите внимание на то, что оказывается еще одной возможной единицей измерения импульса тела).
Словесная формулировка равенства ( 3 ) выглядит следующим образом.
Пример вычисления силы
Проблема. Шар массой g, летящий горизонтально со скоростью м/с, ударяется о гладкую вертикальную стену и отскакивает от нее, не теряя скорости. Угол удара мяча (т.е. угол между направлением движения мяча и направлением, перпендикулярным стене) составляет. Воздействие длится с. Найдите среднюю силу, действующую на мяч во время удара.
Решение. Сначала покажите, что угол отражения равен углу удара, т.е. что мяч отскакивает от стены под тем же углом (рис. 3).
Рисунок 3. Проблема (сверху)
 |
| Проблема здесь в том, что стена гладкая. Это означает, что между мячом и стенкой нет трения. Поэтому единственная сила, действующая со стороны стены на мяч, — это сила упругости, перпендикулярная стене (рис. 4). |
Рисунок 4. проблема
 |
| Согласно ( 3 ) мы имеем: Из этого следует, что вектор изменения импульса совпадает с вектором, т.е. он перпендикулярен стене в направлении отскока мяча (рис. 5). |
Рис. 5. Проблема
 |
| Векторы и и равны по модулю (так как скорость шарика не изменилась). Поэтому треугольник, образованный векторами, и, является равнобедренным. Таким образом, угол между векторами и равен, т.е. угол отражения фактически равен углу падения. |
Теперь обратите внимание, что у нашего равнобедренного треугольника есть угол (это угол падения); следовательно, этот треугольник является равносторонним. Поэтому:
Средняя сила, действующая на сферу, — это то, что мы ищем:
Физическая величина, равная произведению массы тела и скорости его движения, называется импульсом тела или величиной движения тела. Импульс тела обозначается p:
ИМПУЛЬС ТЕЛА
Когда тело находится в состоянии покоя, его импульс равен нулю. Импульс тела — это векторная величина. Направление вектора импульса совпадает с направлением вектора скорости тела. Здесь мы думаем о теле как о материальной точке.
И. Ньютон сформулировал свой закон следующим образом: «Изменение величины движения пропорционально приложенной движущей силе и происходит в направлении прямой линии, на которую эта сила действует».
ИМПУЛЬС ТЕЛА И ВТОРОЙ ЗАКОН НЬЮТОНА
Из формулы (1) мы действительно можем вывести:

Под «изменением величины движения» Ньютон подразумевал изменение импульса тела, поэтому второй закон Ньютона может быть переформулирован следующим образом: Изменение импульса в единицу времени равно силе, действующей на тело.
С помощью этого закона можно выразить зависимость между импульсом силы и изменением импульса тела:
Строго говоря, математическая формулировка второго закона Ньютона применима к случаю, когда сила, действующая на тело, постоянна в течение всего времени его действия, то есть не меняется ни по направлению, ни по величине.
Объясняя свой второй закон, Дж. Ньютон писал: «Если сила имеет O
РЕШЕНИЕ ЗАДАЧИ