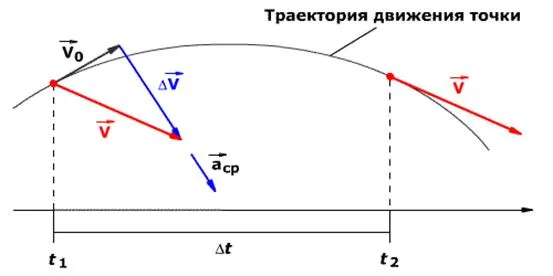
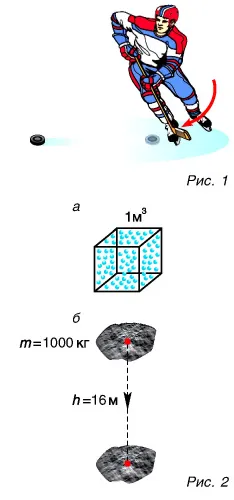
Первый был построен в 1656 году голландским ученым Христианом Гюйгенсом. Это было значительным улучшением по сравнению с существующими механическими часами. Их точность повысилась с 15 минут до 15 секунд в день. Маятники распространились по всей Европе, поскольку все существующие часы были модифицированы.
Математический маятник
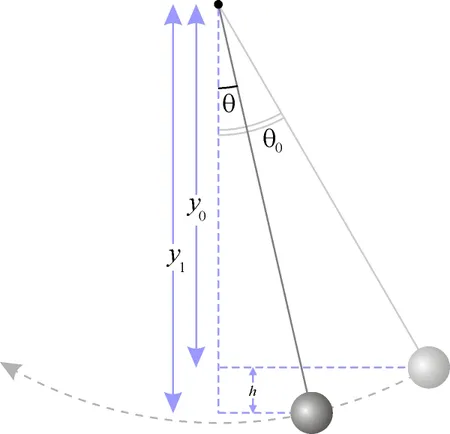
Математический маятник — это осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой, нерастяжимой струне или стержне в однородном гравитационном поле1. Период малых собственных колебаний математического маятника длины L, устойчиво подвешенного в однородном гравитационном поле с гравитационным ускорением g, равен
и не зависит от амплитуды и массы маятника.
Плоский математический маятник со стержнем — это система с одной степенью свободы. Однако если стержень заменить натяжной нитью, то получится система с двумя степенями свободы с муфтой. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
Решения уравнения движения
Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обычным DT второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координаты и скорость, из которых получаются две независимые константы:
Где — начальная фаза колебания,
Нелинейный маятник
Для маятника, который качается с большой амплитудой, закон движения более сложен:
= \varkappa \cdot \operatorname (\omega t | \varkappa),» width=»» height=»» />
где — синус Якоби. Ведь это то же самое, что и обычный тригонометрический синус.
Параметр
,» width=»» height=»» />
где » width=»» height=»» />- энергия маятника в единицах t-2 .
Период колебаний нелинейного маятника
\Omega = \frac<\pi>\Frac<\omega>,» width=»» height=»» />
где K — эллиптический интеграл первого рода.
Для практических расчетов удобно разложить эллиптический интеграл в ряд:
<\left(2n - 1\right)!!><\left(2n\right)!!>\right^2 \sin^\left(\frac\right) + \dots \right\>» width=»» height=»» />, где » width=»» height=»» />ight)^2 \sin^\links(\frac
ight) + \links(\frac
\sin^\left(\frac\right) \right)» width=»» height=»» />.
ight)^2 \sin^\links(\frac
\sqrt\frac,» width=»» height=»» />
ight) + \dots + \left\frac
Движение по сепаратрисе
— период малых колебаний,
Интересные факты
Для углов до 1 радиуса (≈60°) с приемлемой точностью (погрешность менее 1%) можно ограничиться первым приближением:
- Если амплитуда колебания маятника близка к π, то есть, движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения.
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
Простая гравитация
Точная формула для периода, с квадратичной сходимостью для каждого угла максимального отклонения, обсуждается на страницах 1096-1097 сентябрьского выпуска «Записок Американского математического общества» за 2012 год.3:
- Стержень или нить, на котором качается отвес, не имеет массы и не может растягиваться.
- Груз — это точечная масса.
- Движение происходит только в двух измерениях, то есть отвес не может очертить эллипс, а только дугу.
- Энергия движения не расходуется на трение или сопротивление воздуха.
- Гравитационное поле однородно.
- Поддержка всей конструкции не двигается.
Где
Движение маятника вдоль разделительной матрицы является непериодическим. В бесконечно удаленный момент она начинает падать из крайнего вершинного положения в одну сторону с нулевой скоростью, постепенно поднимается, останавливается и возвращается в исходное положение.
Несмотря на свою простоту, математический маятник связан со многими интересными явлениями.
Так называемый простой маятник является лишь идеализированной математической моделью. Это груз на конце безмассовой струны, подвешенной к оси без трения. Если вы находитесь в
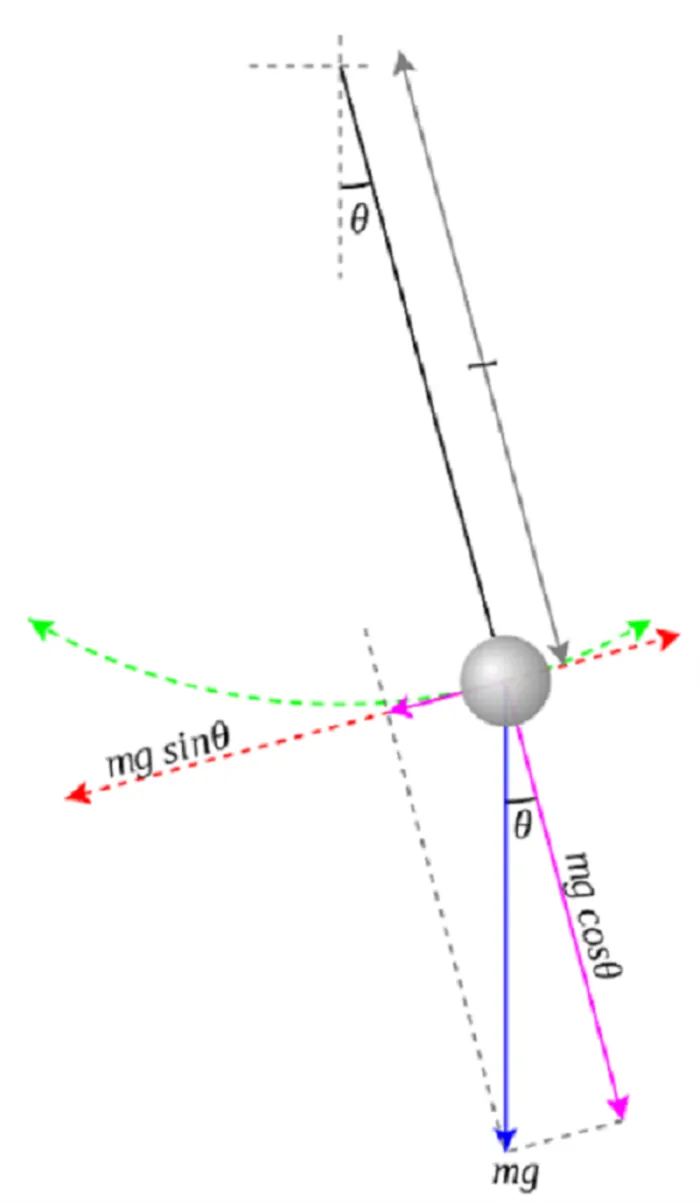
Направление мгновенной скорости всегда задается вдоль красной оси, которая считается тангенциальной, поскольку ее направление всегда касается края. Прежде чем вывести уравнение силы, следует вспомнить второй закон движения Ньютона: F = ma. F — сумма сил, действующих на объект, m — масса, a — ускорение.
Крутящий момент
Поскольку нас интересует только измерение скорости, а груз вынужден оставаться на круговой траектории, уравнение Ньютона применимо только к тангенциальной оси. Короткая фиолетовая стрелка представляет собой компонент гравитационной силы, величину которого мы можем определить с помощью тригонометрии. Это дает (g — ускорение из-за силы тяжести у поверхности Земли) F = — mg sin θ = ma- a = — g sin θ.
Отрицательный знак в правой части означает, что θ и перпендикулярная линия всегда направлены в противоположные стороны. Это имеет смысл, потому что если маятник качается больше влево, то ожидается, что при движении назад он будет ускоряться вправо. Это линейное ускорение a вдоль красной оси может быть связано с изменением угла θ формулами для длины дуги (s): s = ℓθ; v = ds / dt = ℓdθ / dt; a = d²s / dt² = ℓd²θ / dt². Отсюда следует, что ℓd²θ/dt² = — gsin θ, d²θ / dt² + d / ℓ sin θ = 0.
Во-первых, эта экспонента должна быть определена в месте соединения маятника с помощью силы (Fg), вызванной гравитацией: T = ℓ x Fg, где ℓ — вектор длины маятника.
Колебательные движения
Здесь самое время рассмотреть величину крутящего момента на маятнике: |T| = — mgℓ sinθ, где m — масса, g — ускорение из-за силы тяжести, ℓ — длина и θ — угол между вектором длины и силой тяжести. Затем наступает время переписать импульс: L = r x p = mr x (ꞷ x r).

Только величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех расчетов выглядит следующим образом: T = r x F = dL / dt.
Период колебаний математического маятника (простого гравитационного маятника) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, на который перпендикуляр отклоняется от перпендикуляра θ 0, называемого амплитудой.
Она не зависит от массы заряда. Если амплитуда ограничена небольшим колебанием, то время, необходимое для полного цикла, составляет для периода T: T≈ 2 π √ L/g. В данном случае L — длина маятника, а g — местное ускорение под действием силы тяжести.
Следует отметить, что для малых колебаний период не зависит от амплитуды. Это свойство называется изохронностью, и именно поэтому маятники используются для измерения времени. Последовательные колебания маятника, даже если они отличаются по амплитуде, длятся одинаковое время. Характерной особенностью длинных колебаний является то, что период увеличивается с каждым колебанием.
- плавучесть и вязкостное сопротивление воздуха;
- масса нити или стержня;
- размер и форма отвеса и способы его прикрепления к шнуру;
- гибкость и растяжение нити.
Формула математического маятника в малых колебаниях при приближении к гармоническому осциллятору и его движение как функция времени t выражается как θ(t) = θₒ cos (2 π / T * t + ⱷ), где phi (ⱷ) — константа, зависящая от начальных условий. В случае с маятниками, например, этот период времени немного варьируется в зависимости от определенных факторов:
Составной маятник
Если требуются точные расчеты, все эти поправки, конечно, должны быть учтены.

Другое название, физическое, обозначает любое колеблющееся твердое тело, свободно вращающееся вокруг неподвижной горизонтальной оси. Соответствующая эквивалентная длина равна L, а расстояние между осью и центром колебаний используется для расчета времени. Эта точка расположена над центром масс на расстоянии от оси, традиционно называемом радиусом колебаний, который зависит от распределения веса груза.
Христиан Гюйгенс в 1673 году доказал, что центр вращения и центр колебаний взаимозаменяемы. Это означает, что маятник, перевернутый и повернутый в сторону от прежнего центра колебаний, имеет тот же период, что и раньше, а новый центр находится в прежнем центре вращения.