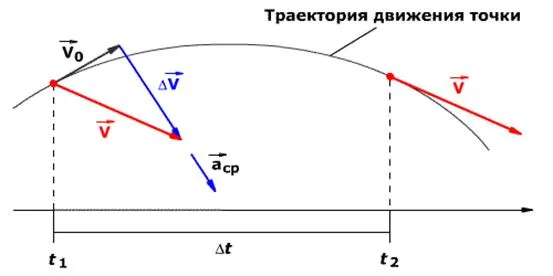
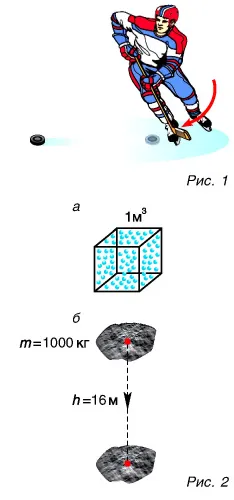
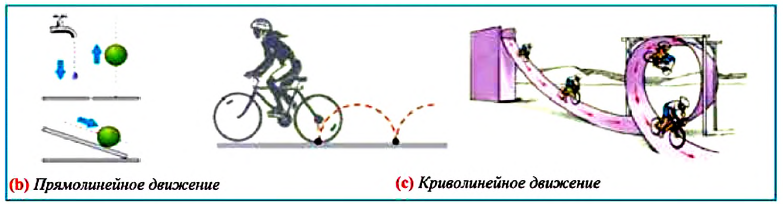
Возьмем точку Q — полюс, относительно которого рассчитывается момент силы. Затем проведите вектор с радиусом r от Q до F, точки приложения. Категория рассчитывается следующим образом:
Момент силы
Момент силы рассматривается в физике как векторная величина, равная векторному произведению радиус-вектора, заданного осью вращения в точке приложения силы, и ее направления.
Категория описывает действие силы по отношению к твердому телу.
Бывает, что велосипедисту приходится поворачивать руль транспортного средства вручную. Это гораздо быстрее, чем захват спиц, так как они находятся ближе к точке поворота. Тяга — это крутящий момент, т.е. вращательное движение.
Осторожно. Если учитель обнаружит плагиат в вашей работе, у вас будут большие неприятности (вплоть до исключения из школы). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Крутящий момент и угловой момент не идентичны, поскольку термин «угловой момент» относится к внешней силе, действующей на объект, а термин «угловой момент» относится к внутренней силе, действующей на объект под действием нагрузки.
В физике крутящий момент интерпретируется как вращение.
В теории эта категория также называется импульсом пары сил, термин, восходящий к работе Архимеда о рычагах. Так, если на рычаг перпендикулярно действует сила, то импульс силы получается умножением величины силы на расстояние от оси вращения рычага.
В линейной механике сила — это мера способности придать телу линейное ускорение. Аналогично, крутящий момент точки — это мера способности придать системе угловое ускорение. Он также придает угловое ускорение — эти два параметра прямо пропорциональны друг другу.
Например, если отодвинуть дверь дальше от дверных петель, то есть туда, где находится ручка, она открывается легче и быстрее. Отсюда видна разница во вращении/вращательной способности. Другой пример. Тяжелый предмет легче удержать, если прижать к нему руку, а не держать ее на вытянутой руке. Таким образом, в приведенных выше случаях импульс силы изменяется по мере уменьшения/увеличения рычага.
Формула для импульса выглядит следующим образом:
M — это импульс силы (также обозначается как t), а dL — изменение импульса за бесконечно малый промежуток времени dt.
Абсолютная величина момента силы
Абсолютное значение импульса силы — это величина, равная произведению абсолютного значения на плечо данной силы относительно выбранной точки.
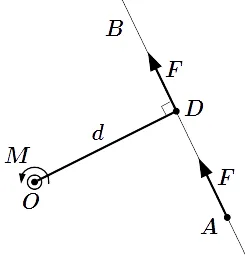
Рассмотрим следующий рисунок.
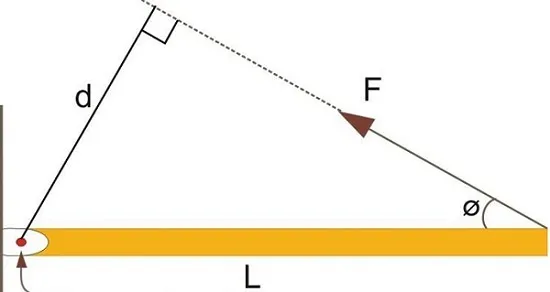
На нем изображен брусок длиной L. Таким образом, он одним концом прикреплен к вертикальной плоскости с помощью шарнира, а другой конец свободен. F¯ действует на него. Угол между
Крутящий момент рассчитывается в ньютонах на метр, т.е. имеет ту же размерность, что и работа и энергия в естественных науках. Однако следует отметить, что это понятие является векторной величиной, которую нельзя рассматривать как работу. Импульс силы совершает работу в соответствии с формулой:
Значение θ указывает центральный угол в радианах, вокруг которого вращается система в данный момент времени t.
В физике крутящий момент можно понимать как «вращающую силу». В системе СИ единицей измерения силы крутящего момента является Ньютон-метр. Момент силы иногда называют моментом пары сил — понятие, заимствованное из работы Архимеда о рычагах. В простейшем случае, когда сила действует на рычаг перпендикулярно, крутящий момент определяется как произведение величины этой силы на расстояние от оси вращения рычага. Например, сила в 3 ньютона на рычаге, находящемся на расстоянии 2 м от оси вращения, создает такой же крутящий момент, как и сила в 1 ньютон на рычаге, находящемся на расстоянии 6 м от оси вращения. Более точно, импульс частицы определяется как векторное произведение
Работа момента силы
где — сила, действующая на частицу, и радиус-вектор частицы.
Строго говоря, вектор, обозначающий момент силы, введен искусственно, так как он подходит для вычисления работы вдоль изогнутого сегмента относительно неподвижной оси и для вычисления общего момента силы всей системы, так как его можно суммировать. Чтобы понять, откуда взялось обозначение импульса и как оно появилось, стоит рассмотреть действие силы на рычаг, вращающийся вокруг неподвижной оси.
Содержание
- 1 Общие сведения
- 2 Предыстория
- 3 Единицы
- 4 Специальные случаи
- 4.1 Формула момента рычага
- 4.2 Сила под углом
- 4.3 Статическое равновесие
- 4.4 Момент силы как функция от времени
Работа, совершаемая под действием силы вокруг неподвижной оси, может быть вычислена с помощью следующих соображений.
\times\vec\right» width=»» height=»» />
Пусть под действием силы конец рычага пройдет бесконечное расстояние. Обозначим равенством вектор и вектор силы.
Предыстория
Поэтому бесконечно малая работа в бесконечно малой части и вектор силы, т.е.
Теперь попробуем выразить коэффициент вектора, и проекцию вектора силы
или
ight| \sin
Теперь мы видим, что произведениеТак как для бесконечно малого перемещения рычага, используя соотношения для прямоугольного треугольника, можно записать следующее равенство:, где в случае малого угла справедливо и следовательно \right| d\varphi» width=»» height=»» />
Для проекции вектора силы, видно, что угол » width=»» height=»» />, а так как \right )>= \sin» width=»» height=»» />, получаем, что = \left| \vec \right| \sin» width=»» height=»» />.
Теперь запишем бесконечно малую работу через новые равенства \right| \sin» width=»» height=»» />ight| \sin<\left (\alpha \right )>d\varphi» width=»» height=»» />.
это не что иное, как мера векторного произведения векторов, т.е. мера вектора силы-момента.<\left (\alpha \right )>» width=»» height=»» />Теперь вся работа написана очень просто: …
Момент силы — это сила, действующая на расстояние, и в системе СИ единицей измерения момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, также определяется как 1 Н-м, но эта единица не используется для крутящего момента. Когда энергия представлена как результат «сила умноженная на перемещение», энергия является скалярной, в то время как момент силы — это «сила, умноженная на перемещение векторно» и, таким образом, a (
Единицы
В предыдущей теме мы говорили о простых механизмах, которые изменяют механическое воздействие на тело путем изменения точки приложения силы, ее величины и направления. Мы выяснили, что рычаг — это любое твердое тело, которое может вращаться относительно неподвижной опоры или оси.
,
Мы различаем два типа рычагов: рычаг первого типа и рычаг второго типа. Рычаг первого рода — это рычаг, ось вращения которого лежит между точками приложения сил, а сами силы направлены в одну сторону. Рычаг второго типа — это рычаг, ось вращения которого лежит по одну сторону от точек приложения сил, а сами силы действуют в противоположных друг другу направлениях. Расстояние между точкой контакта и линией, вдоль которой действует сила, называется плечом рычага.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Мы вывели условие равновесия рычага, согласно которому рычаг находится в равновесии, если действующие на него силы обратно пропорциональны длинам их плеч.
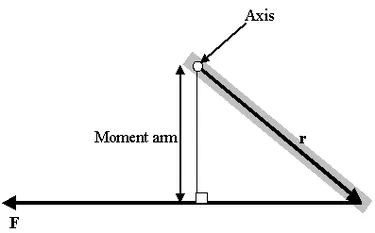

Применим основное свойство пропорциональности к состоянию равновесия рычага. Тогда условие равновесия рычага имеет следующий вид

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Момент силы»
Произведение коэффициента силы и плеча рычага дает новую физическую величину — момент силы (обозначается M).
Крутящий момент измеряется в Ньютон-метрах (Н-м).
Момент силы описывает действие силы и показывает, что это действие зависит как от величины силы, так и от рычага.
Сформулируем условие равновесия рычага, используя правило моментов: рычаг находится в равновесии под действием двух моментов, если момент силы, поворачивающей рычаг по часовой стрелке, равен моменту силы, поворачивающей его против часовой стрелки.
В эксперименте, описанном в предыдущем разделе, силы, действующие на рычаг, были 8 Н и 4 Н соответственно, а их плечи составляли 2,5 и 5 делений рычага соответственно. Это означает, что в равновесии рычага моменты этих сил равны.
Можно ли уравновесить рычаг, когда на него действует более двух сил? Да, это так. Посмотрите на иллюстрацию.
Это изображение рычага с различными силами, действующими на него. Для того чтобы такой рычаг был в равновесии, нам необходимо:
1. найдите сумму моментов всех сил, которые вращают рычаг по часовой стрелке.
Обратите внимание, что плечо силы F
— не является прямой OC, а прямая OB является кратчайшим перпендикуляром к прямой CB .
2. найдите сумму моментов сил, поворачивающих рычаг против часовой стрелки.
3. сравните сумму моментов всех сил, которые поворачивают рычаг по часовой стрелке, с суммой моментов сил, которые поворачивают рычаг против часовой стрелки.
И если эти суммы равны, то рычаг находится в равновесии.
Твитнуть

5
3