На этом уроке мы вспомним, какое движение называется движением с равным ускорением. Мы рассмотрим формулы для определения скорости тела, его координат, пути и перемещения при движении по плоскости. Мы также рассмотрим графическое представление временной зависимости кинематических величин в этом типе движения.
Основные определения
Ускорение — это физическая величина, которая описывает степень изменения скорости объекта. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, насколько изменяется скорость за одну секунду.
Линейное равномерно ускоренное движение — это движение, при котором скорость тела изменяется на одинаковую величину за равные промежутки времени. Под «изменениями» мы подразумеваем не только ускорение (т.е. увеличение скорости), но и замедление. Замедление также относится к движению с постоянным ускорением.
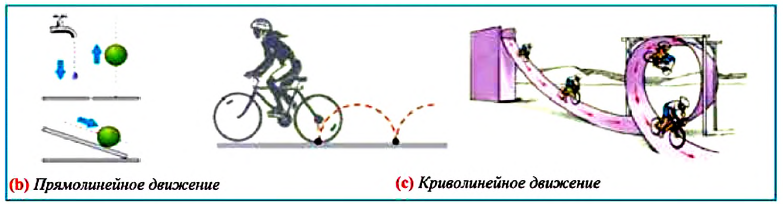
Примерами равномерно ускоренных движений являются:
- разгон самолета перед взлетом;
- торможение лыжника на горном склоне;
- свободное падение в результате прыжка с парашютом;
- велосипедист, спускающийся с горки;
- мальчишки, играющие в догонялки.
Кстати, уже известное равномерное прямолинейное движение является частным случаем равномерного ускорения, где ускорение равно нулю.
Формула для ускорения равномерно ускоренного движения имеет вид
где a — ускорение тела м/с 2, V — мгновенная скорость м/с, V0— начальная скорость м/с, t — время с.
Пока тело находится в движении, ускорение остается постоянным. График ускорения как функции времени имеет следующий вид:

Для прямолинейного равномерно ускоренного движения скорость тела в момент времени t численно равна площади фигуры под графиком зависимости между ускорением и временем.
Если выразить мгновенную скорость, т.е. скорость в момент времени t, через формулу ускорения, то мы получим уравнение скорости для равномерно ускоренного движения:
V(t) = V0+ at, где V(t) — скорость в момент времени t м/с, V0— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
Задача 1
Арсений ехал на электросамокате с горки со скоростью 6 м/с. Какова будет его скорость через 10 с, если ускорение во время разгона равно 0,5 м/с 2?
Решение.
Согласно задаче, Арсений разгоняется так, что его скорость увеличивается. Подставим числа в закон изменения скорости при равновесном ускорении:
V(10) = 6 + 0,5 — 10 = 11 м/с.
Ответ: Арсений разгонится до 11 м/с за 10 с.
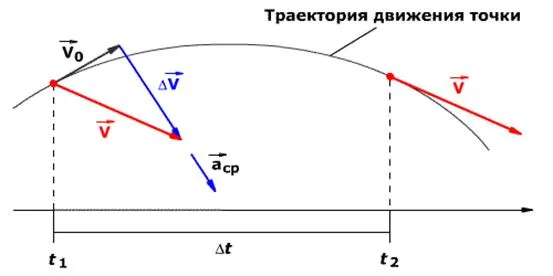
Важно знать, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет тип движения. Посмотрите на анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т.е. ускоряется. В то же время синий автомобиль снижает скорость и тормозит. В случае a движение называется изоускоренным
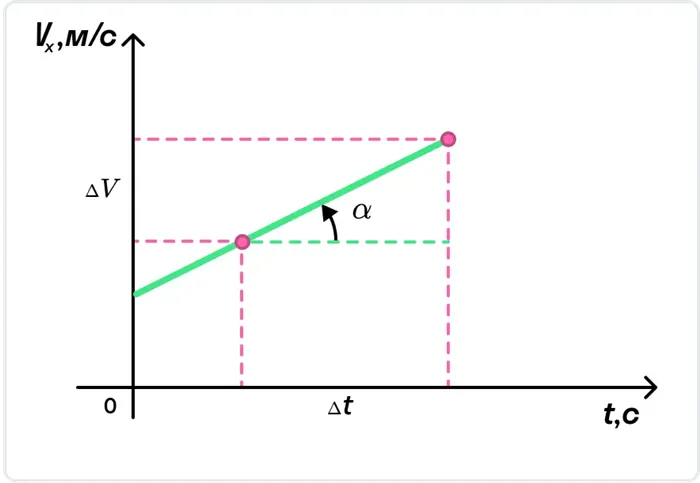
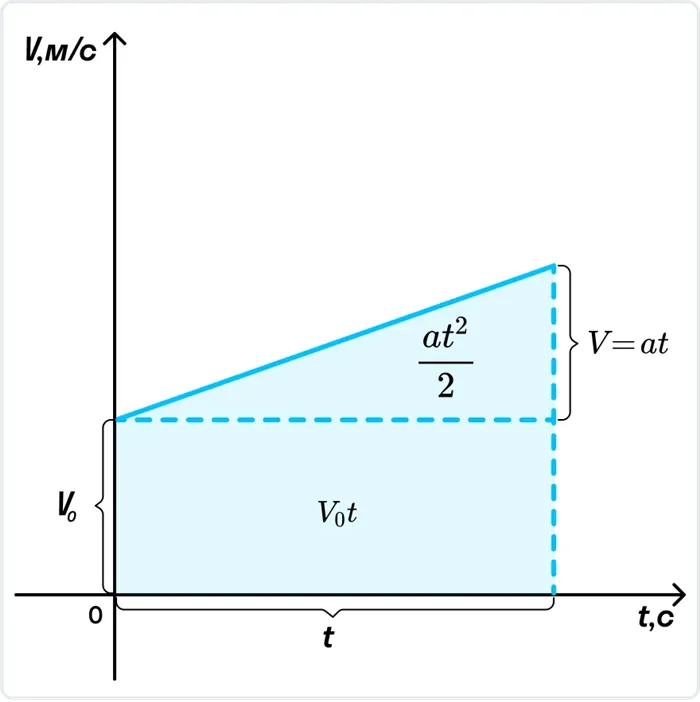
График зависимости скорости от времени при равноускоренном движении
Расстояние, пройденное телом при плоском движении, численно равно площади фигуры под диаграммой «скорость-время». Вычислим площадь трапеции как сумму площадей прямоугольника V
t и треугольник .0).
Формула для траектории равномерно ускоренного движения имеет вид
где S — расстояние, пройденное за время t м, V
— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
Для равномерно ускоренного движения с неизвестным временем пробега, но заданными начальной и конечной скоростями, пройденное расстояние можно найти по следующей формуле:0где S — расстояние, пройденное за время t м, V
— начальная скорость м/с, V — скорость в момент времени t м/с, a — ускорение тела м/с 2 .
Водитель такси Роман получил заказ и после длительной остановки начал движение с ускорением 0,1 м/с 2. На каком расстоянии от начала движения его скорость будет равна 15 м/с?0— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
Ответ: На расстоянии 1 125 м от начала движения скорость такси составит 15 м/с.
Водитель такси Роман получил заказ и после длительной остановки начал движение с ускорением 0,1 м/с 2. На каком расстоянии от начала движения его скорость будет равна 15 м/с?0Путь — это длина траектории. Когда тело движется в любом направлении, его путь увеличивается. Шагомер на вашем телефоне или смарт-часах измеряет пройденный путь. Чтобы вычислить путь по графику скорости, нужно найти площади каждой фигуры и сложить их вместе, как показано выше.
Задача 2
Перемещение — это вектор, соединяющий начальное и конечное положения тела. Чтобы найти смещение по диаграмме скоростей, нужно взять площади над осью времени со знаком «+» и под осью со знаком «-«, а затем просуммировать их.
Решение.
- По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
- Поскольку время движения неизвестно, то определим путь по второй формуле:
- Подставим числа и выполним расчет: м.
а перемещение — S
Перемещение при равноускоренном движении
Уравнение для перемещения при равномерно ускоренном движении имеет вид
где S — перемещение в момент времени t м, V
— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
Вы, вероятно, заметили удивительное сходство формул расстояний в движении плоскости. Да, но помните, что проекция смещения может принимать отрицательное значение, а расстояние — нет. В некоторых задачах расстояние и смещение могут совпадать, но не всегда.1+ S2Важнейшей задачей кинематики является определение положения тела относительно других тел с течением времени. Для решения этой задачи необходимо знать связь между координатами и временем (уравнение движения).1− S2.
Уравнение равномерного ускорения
где x(t) — координата в момент времени t m, x0— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
где S — расстояние, пройденное за время t, V0 — начальная скорость, V — скорость за время t и α — ускорение тела.
Водитель такси получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость составляет 15 м/с? Решение. Когда водитель такси начал движение, начальная скорость была равна нулю (Vn=0), Vk=15м/с, ускорение a=0,1м/с2. Мы получаем: На расстоянии 1 125 м от начала движения скорость такси равна 15 м/с.
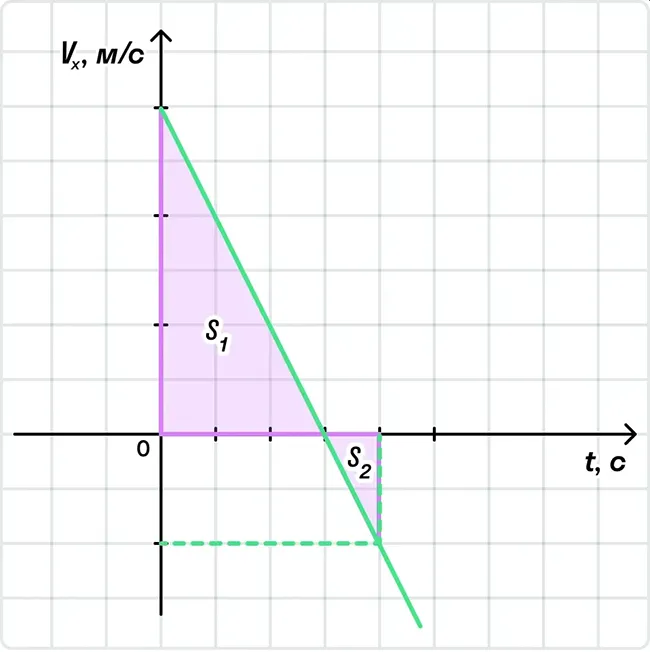
Важно помнить о разнице между движением и перемещением тела.
Например, если путешественник проходит расстояние S1 с одной стороны и S2 с другой, то смещение тела составляет S1 + S2, а перемещение S1 — S2. В некоторых задачах путь и смещение могут совпадать, но не всегда.0Движение, при котором ускорение тела постоянно, называется изоускоренным движением. Знак ускорения не имеет значения. Движение с постоянным отрицательным ускорением также ускоряется равномерно, даже если скорость уменьшается.0— начальная скорость м/с, a — ускорение тела м/с 2, t — время с.
Задача 3
Мы хотим найти формулы для скорости и координат для изохронного ускорения. Из приведенного выше определения ускорения следует, что скорость при постоянном ускорении равна
Решение.
- Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0= 3 м/с. Начальная координата равна нулю.
- Найдем ускорение из формулы пути при равноускоренном движении: м/с 2 .
- Составим уравнение движения лыжника: .
- По уравнению определим координату лыжника в момент времени t = 2 с: м.
Это линейная зависимость. Он представлен в виде прямой линии, наклон которой зависит от значения $a$. Чем он больше, тем круче поднимается кривая.
Из курса физики 9-го класса мы знаем, что перемещение тела равно площади под графиком скорости. А площадь под этой линией — трапеция с высотой $t$ и основаниями $v$ и $v_0$. Как мы знаем из геометрии, площадь трапеции равна произведению половины площади основания на высоту. Это:

a=(Vк-Vн)/t
$\overrightarrow x=
Задача 1
t$
Формула расстояния при равноускоренном движении
S = t* (Vн+ Vк)/2
Подставляя значение $v$ из предыдущей формулы и учитывая, что координата в начальный момент времени была $x_0$, получаем:
Это основная формула равновесия для определения координаты $\overrightarrow x$ материальной точки в момент времени $t$, предполагая, что начальная координата была $\overrightarrow x_0$, начальная скорость $\overrightarrow $ и ускорение $\overrightarrow a$. В проблемах он обычно используется в сочетании с предыдущим.
2аS = Vкн2
Задача 2
Перемещение при равноускоренном движении
Уравнение для перемещения при равномерно ускоренном движении имеет вид
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Равноускоренное движение

Формулы равноускоренного движения
<(\overrightarrow