Здесь лучше сразу увидеть, насколько это проще. Например, 31 × 25 легче умножить обычным способом, то есть 750+25, чем 31 × 25, то есть 7,75 × 100.
Как быстро вычислить степень числа
Теперь мы знаем, что означает степень числа. Теперь нам нужно понять, как правильно их вычислять, то есть как возводить числа в степень. Данный материал охватывает основные правила вычисления степеней для целочисленных, натуральных, дробных, рациональных и иррациональных экспонент. Все определения объясняются на примерах.
Начнем с перечня основных определений.
Возведение в степень — это вычисление значения степени заданного числа.
То есть слова «вычисление значения мощности» и «экспоненция» означают одно и то же. Поэтому если в задании сказано: «Возведите число 0, 5 в пятую степень», то это следует понимать как «Вычислите значение степени ( 0, 5 ) 5».
Давайте теперь упомянем некоторые основные правила, которые необходимо соблюдать при таких расчетах.
Как возвести число в натуральную степень
Вспомните, чему равна мощность числа с натуральной экспонентой. Для степени с основанием a и показателем n она является произведением n множителей, каждый из которых равен a. Это можно записать следующим образом:
Чтобы вычислить значение степени, необходимо выполнить операцию умножения, то есть перемножить основания степени определенное количество раз. Понятие степени с натуральной экспонентой основано на способности к быстрому умножению. Вот несколько примеров.
Необходимое условие: преобразование — 2 в степени 4 .
Решение
Используя приведенное выше определение, запишем: ( — 2 ) 4 = ( — 2 ) — ( — 2 ) — ( — 2 ) — ( — 2 ) — ( — 2 ) — ( — 2 ) — ( — 2 ) — ( — 2 ) Тогда нам остается только проделать описанные выше действия и получить 16 .
Рассмотрим более сложный пример.
Вычислите значение 3 2 7 2
Решение
Этот вход можно переписать как 3 2 7 — 3 2 7. Ранее мы уже рассматривали, как правильно умножать смешанные числа, заданные в предпосылке.
Выполняем указанные выше операции и получаем ответ: 3 2 7 — 3 2 7 = 23 7 — 23 7 = 529 49 = 10 39 49.
Если в задаче требуется округлить иррациональные числа до натуральных чисел, мы должны сначала округлить их основания до такого положения, которое позволит нам получить точный ответ. Давайте рассмотрим пример.
Площадь р .
Решение
Первый раунд до сотой. Тогда π 2 ≈ ( 3, 14 ) 2 = 9, 8596. Если π ≈ 3. 14159, то получаем более точный результат: π 2 ≈ ( 3, 14159 ) 2 = 9, 8695877281 .
Следует отметить, что необходимость вычисления степеней иррациональных чисел возникает на практике относительно редко. Затем мы можем записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Независимо от этого, мы должны указать, что такое первая сила числа. Здесь мы можем просто вспомнить, что любое число, возведенное в первую степень, остается тем же самым:
Это следует из обозначения
Это не зависит от основания степени.
Поэтому ( — 9 ) 1 = — 9 и 7 3, возведенное в первую степень, остается 7 3 .
Как возвести число в целую степень
Для простоты мы рассмотрим три случая отдельно: когда экспонента является положительным целым числом, когда она равна нулю и когда она является отрицательным целым числом.
5 0 = 1, ( — 2, 56 ) 0 = 1 2 3 0 = 1
0 0 не определено.
Остается случай степеней с отрицательной целочисленной экспонентой. Мы уже видели, что эти степени можно записать в виде дробей 1 a z, где a — любое число, а z — отрицательная целая экспонента. Мы видим, что знаменатель этой дроби — не что иное, как обычная сила с положительной целочисленной экспонентой, и мы уже научились ее вычислять. Вот несколько примеров проблем.
Расширьте 2 до степен и-3.
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3.
Решение
Тогда ответ: 2 — 3 = 1 2 3 = 1 8 .
Умножьте 1,43 на — 2.
Решение
Переформулируем: 1, 43 — 2 = 1 ( 1, 43 ) 2
Решение
Наконец, ( 1, 43 ) — 2 = 1 ( 1, 43 ) 2 = 1 2, 0449. Теперь запишем этот результат в виде дроби и умножим его на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1, 43 ) — 2 = 10000 20449
Частным случаем является увеличение числа до степени минус 1. Значение этой степени равно числу, которое является обратным исходному значению основания: a — 1 = 1 a 1 .
Пример: 3 — 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
При умножении «умножить» означает, что число и экспонента положительны. Мы покажем вам, как преобразовывать числа в силы на примере, используя калькулятор!
Для целого числа, положительного числа и силы — Правило возведения числа в степень следующее:
Как возвести в степень
Чтобы возвести число в степень, умножьте его на само себя во столько раз, во сколько раз больше значение степени.
Начнем с простейшего случая умножения, где автоматически предполагается, что число и сила положительны!
Пример экспоненты: скажем, 3 в степени 3, 3 в степени 3 можно представить как 3 в степени 3, умножить на 1 и получить 27.
Чтобы умножить число с помощью калькулятора, вам действительно нужен калькулятор и пример на умножение! И как было сказано выше, умножение имеет свое собственное имя. Хотя — это всего лишь вторая сила!
Нам нужен пример, и мы сделаем его равным пяти в степени три:
Мы вводим число, которое хотим возвести в степень 5.
Нажмите клавишу степени и букву «P».
Введите значение мощности, число — 3.
Теперь мы получим результат сложения числа в степени с помощью нашего калькулятора:
Решение алгебраических выражений — одна из самых распространенных задач в высшей математике. И как всегда, успех и правильный ответ зависят от
Нажимаем кнопку равно — » https://dwweb.ru/__img/calc/a/0029_vozvedenie_v_stepen_2020_10_02_11_19.png» alt=»Пример возведения в степень на калькуляторе.» title=»Пример возведения в степень на калькуляторе.»>
Например, если задача состоит в вычислении (0,4)^4, существует другая, не менее правильная формулировка: «Умножить 0,4 на силу 4». Затем мы можем перейти непосредственно к правилам, по которым выполняется эта математическая операция.
Как возвести число в натуральную и дробную степень
Согласно самому определению, мощность числа a с n — натуральный коэффициент — равна произведению n коэффициентов, каждый из которых в свою очередь равен a. Другими словами, чтобы возвести число a в степень n, необходимо вычислить произведение вида a*a. *а делится на n. Итак, ясно, что умножение на степень n (то есть на натуральное число) опирается на умение умножать числа, а как именно это делать, вы можете узнать, прочитав раздел об умножении действительных чисел.
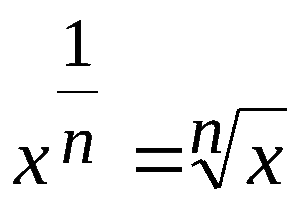
Что означает возведение в степень
Мы опишем решение на нескольких примерах.
Что касается приведения иррациональных чисел к натуральной степени, то это следует делать в конце подготовительного округления основания силы до определенной степени, позволяющей вывести значение с некоторой точностью.

Натуральная степень числа
Следует отметить, что многие задачи не требуют экспоненты иррациональных чисел. Обычно ответ дается либо в виде самой силы, например, (ln6)^3, либо, если возможно, путем преобразования выражения: корень из 5 в степени 7 — сто двадцать пять.
В выражениях, не содержащих круглых скобок, сначала выполняется умножение, затем умножение и деление в порядке старшинства, а затем сложение и вычитание в порядке старшинства.
- Пример 1. Задача Требуется выполнить возведение числa минус два в cтепень 4. Решение задачи. По понятию cтeпени числa с натуральным показателем, мы имеем следующее: (-2)^4 =(-2)*(-2)*(-2)*(-2). Все очень просто. Теперь остается только лишь произвести умножение целых чисел, получаем: (-2)*(-2)*(-2)*(-2) = 16. Записываем ответ: (-2)^4 = 16.
- Пример 2. Определите значение степени: ( 3 2/7 )^2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
Иррациональные числa
Пример 1. Найдите значение выражения 2 + 5 2. Сначала умножьте число: 5 2 = 25. Прибавьте этот результат к числу 2: 2 + 5 2 = 2 + 25 = 27.
- К примеру, нам следует возвести в квадрат числo пи.
- Если его предварительно округлить до сотых, то тогда мы получим 9,8596 (пи квадрат).
- Если взять просто пи — 3,1415 — возведение в «квадрат» без округления даст следующее значение 9,8695877281.
Пример 2: Найдите значение выражени я-6 2 × (-12) Сначала выполним умножение: Обратите внимание, чт о-6 не заключено в круглые скобки, поэтому число 6 возводится во вторую степень, а перед результатом ставится знак минус: -6 2 = -36 Затем умножаем результат на (-12): -6 2 × (-12) = -36 × (-12) = 432

Нахождение значений выражений
Если выражение содержит круглые скобки, то сначала выполняются операции над скобками, затем умножение и деление, затем сложение и вычитание.
Пример 3: Найдите значение выражения (3 2 + 1 × 3) — 15 + 5 Сначала выполните операции внутри скобок. Внутри скобок нужно применить правила, которые мы изучили ранее, то есть сначала умножить 3 на вторую силу, затем умножить 1 × 3, а затем сложить результаты умножения 3 и умножения 1 × 3. Вычитание и сложение выполняются в следующем порядке: (3 2 + 1 × 3) — 15 + 5 = 12 — 15 + 5 = 2
Пример 2 7 :2 3 = 2 7-3 = 2 4
Если уклон увеличивается на одну точку, основание склона остается неизменным
a n : a m = a n — m
a — любое число, не равное нулю m, n — любые натуральные числа такие, что m>n








