Чтобы вычислить количество рациональных чисел, необходимо найти мощность их количества. Легко доказать, что множество рациональных чисел является счетным. Все, что необходимо, — это разработать алгоритм, который подсчитывает рациональные числа, то есть устанавливает границу между множествами рациональных и натуральных чисел.
Числа. Рациональные числа.
Рациональное число — это число, представленное обычной дробью m/n, где числитель m — целое число, а знаменатель n — натуральное число, например, 2/3.
Какие числа являются логическими числами? Рациональные числа (в отличие от иррациональных) — это числа с положительным или отрицательным знаком (целые и дробные) и нулем. Более точное представление о рациональных числах следующее:
Рациональное число — это число, представленное обычной дробью m/n, где числитель m — целое число, а знаменатель n — натуральное число, например, 2/3.
Бесконечные непериодические дроби НЕ принадлежат множеству рациональных чисел.
Поэтому число π (π = 3,14…), основание натурального логарифма, e (e = 2,718…) или √2 не являются рациональными числами.
Логические числа, примеры:
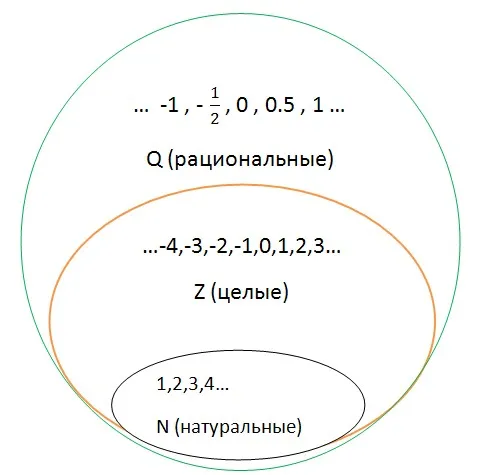
Множество рациональных чисел.
Множество рациональных чисел обозначается
Кроме того, дробь можно записать по-разному, но смысл от этого не теряется. Например, 3/4 и 9/12 (любая дробь, которую можно получить из другой дроби (и наоборот) путем умножения или деления числителя и знаменателя на одно и то же натуральное число, является одним и тем же рациональным числом). Поскольку при делении числителя и знаменателя дроби получается единственное представление рационального числа, которое не может быть сокращено, можно говорить о множестве несводимых дробей с взаимно простыми целыми числителями и натуральными знаменателями:
Множество рациональных чисел является естественным обобщением множества целых чисел. Если рациональное число a=m/n имеет знаменатель n=1, то a=m — целое число.
Любое рациональное число можно легко выразить в виде дроби, где числитель — целое число, а знаменатель — натуральное число.
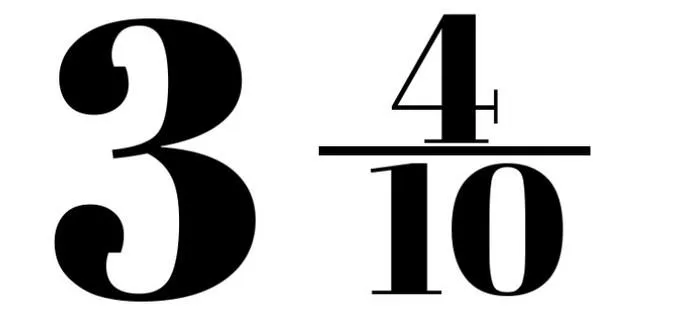
Использование рациональных чисел в реальной жизни.
В реальной жизни набор рациональных чисел используется для подсчета частей некоторых делимых целочисленных объектов, таких как пирожные или другие продукты, которые разрезаются на части перед употреблением, или для аппроксимации пространственных отношений некоторых протяженных объектов.
Фундаментальные свойства рациональных чисел.
1.Порядок.. Для любых рациональных чисел a и b существует правило, позволяющее однозначно определить 1 и только 1 из 3 отношений между ними: «» или «=». Это правило является правилом упорядочивания и формулируется следующим образом:
2.Функция сложения. Для всех рациональных чисел a и b существует правило сложения, которое присваивает им определенное рациональное число c. Само число c является уникальным присвоением числа c числу c. Само число c является уникальным присвоением числа c числу c.
. Существует рациональное число 0, добавление которого сохраняет все остальные рациональные числа.
3.Существование противоположных чисел. Каждое рациональное число имеет противоположное рациональное число; их сложение дает 0.
4.Коммутативность умножения. Если поменять местами рациональные множители, то произведение не изменится.
5.10.Связность умножения .
6.. Порядок умножения трех рациональных чисел не влияет на сумму.11.
7.Присутствие. Существует рациональное число 1, которое при умножении сохраняет все остальные рациональные числа.
8.12.Наличие обратных чисел
9.. Каждое рациональное число, кроме нуля, имеет обратное рациональное число, умножение на которое дает 1.13.
Дистрибутивность умножения по отношению к сложению .. Операция умножения связана со сложением распределительным законом:14.
Отношение отношения порядка к акту сложения .. К левой и правой части логического неравенства прибавляется одно и то же логическое число.15.
Связь между отношением порядка и операцией умножения .. Левая и правая части логического неравенства могут быть умножены на одно и то же неотрицательное логическое число.16.
Аксиома Архимеда .. Независимо от логического числа a, легко получить столько единиц, чтобы их сумма была больше a .Предположим, что a, b и c — произвольные рациональные числа.
a + b = b + a, например: 2 + 3 = 3 + 2?a + (b + c) = (a + b) + c, например: 2 + (3 + 4) = (2 + 3) + 4?a + 0 = a, например: 2 + 0 = 2;
a + (- a) = 0, например: 2 + (- 2) = 0a × b = b × a, например, 2 × 3 = 3 × 2a × (b × c) = (a × b) × c, например, 2 × (3 × 4) = (2 × 3) × 4
a × 1 = a, например, 2 × 1 = 2a × 1/a = 1, если a ≠ 0 — например, 2 × 1/2 = 1a × 0 = 0, например, 2 × 0 = 0
Свойства рациональных чисел
a × b = 0, поэтому: либо a = 0, либо b = 0, либо оба равны нулю.
Переместительные и сочетательные законы
(a + b) × c = a c + b c например: (2 + 3) × 4 = 2×4 + 3×4
(a — b) × c = a c — b c например: (3 — 2) × 4 = 3×4 — 2×4
Иррациональные числа являются противоположностью рациональных чисел, то есть числа, которые НЕ могут быть записаны в виде простых дробей.
Множество иррациональных чисел обозначается «I».
Переместительные и сочетательные законы при умножении
Целые числа — это натуральные числа, противоположные числа (меньше нуля) и ноль.
Все целые числа являются рациональными числами (включая натуральные числа), поскольку их можно представить в виде дроби.
Множество целых чисел обозначается в математике буквой Z.
Натуральные числа — это только целые числа, которые начинаются с 1.
Такая нумерация возникла естественным образом, когда люди еще считали пальцами и не знали никаких цифр («У меня столько коз, сколько пальцев на обеих руках»), поэтому ноль не является натуральным числом.
Множество натуральных чисел обозначается в математике буквой N.
Распределительный закон умножения
Существует несколько групп рациональных чисел.
Натуральные числа — это все целые числа, которые имеют mi
Иррациональные числа
Исторически целые числа возникли как решение проблемы конечности натуральных чисел. С развитием математики стало известно о существовании нуля и отрицательных чисел. Однако множество Z не содержит дробных чисел. Он замкнут относительно всех операций, кроме деления.
- число Пи = 3,14159. его можно записать как 22/7, но это будет лишь приблизительно и далеко не точно ( 22/7 = 3,142857..);
- √2 и √99 — иррациональные, т. к. их невозможно записать дробью (корни часто иррациональные, но не всегда);
- e (число) = 2,72 — иррациональное, т. к. его невозможно записать дробью;
- золотое сечение φ=1,618. — иррациональное, т. к. его невозможно записать дробью.
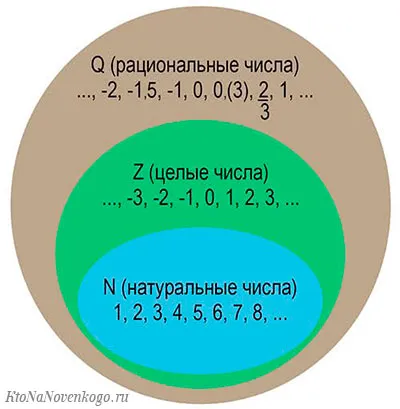
Множество рациональных чисел по определению является самым большим из трех множеств. Она включает в себя все натуральные и целые числа.
Какая разница между целыми, натуральными и рациональными числами
Система отношений между множествами может быть представлена в виде эйлеровой окружности. Система показана ниже.
Насколько полезной для вас была эта статья?
Мы уже писали, что почти все возможные варианты подпадают под понятие рациональных чисел. Теперь рассмотрим имеющиеся варианты подробнее:
Натуральные числа
Все числа, которые подпадают под понятие рациональных чисел, называются РАЦИОНАЛЬНЫМИ ЧИСЛАМИ. В математике его обычно обозначают латинской буквой Q.
Графически это можно представить следующим образом:
Рациональные числа подчиняются всем основным законам математики:
Классификация рациональных чисел, виды с примерами
Для интереса можно попробовать заменить буквы на цифры, чтобы проверить, действуют ли эти законы.
- Целые числа.
- Обыкновенные дроби.
- Десятичные дроби:
- конечные: после запятой стоит определенное количество цифр — например, 0,6; -4,657;
- бесконечные периодические: после запятой стоит бесконечное количество цифр, но одна или несколько из них повторяются. Такие повторяющиеся цифры называют периодом. Их записывают в скобках для краткости: \(0,33333\dots=0,\left(3\right).\)
Какая разница между целыми, натуральными и рациональными числами
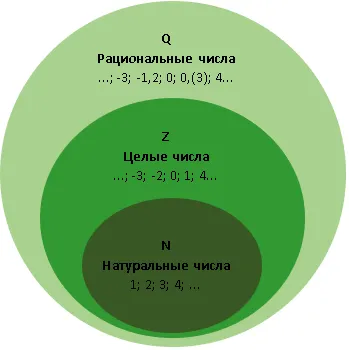
Разновидности рациональных чисел
- Натуральные числа. Любое число с 1 и до бесконечности можно представить в виде дроби. Достаточно вспомнить простое математическое правило. Если поделить число на единицу, то получится то же самое число. Например, 5 = 5/1, 27 = 27/1, 136 = 136/1 и так далее.
- Целые числа. Точно такая же логика, как в случае с натуральными числами, действует и тут. Отрицательные числа также можно представить в виде дроби с делением на единицу. И точно также будет в отношении нуля. Например, -356 = -356/1, -3 = -3/1, 0 = 0/1 и так далее.
- Обыкновенные дроби. Это напрямую говорится в определении рациональных чисел. Например, 6/11, 2/5, -3/10 и так далее.
- Бесконечные периодические дроби. Это числа, у которых после запятой бесконечное множество знаков и их последовательность повторяется. Самые простые примеры 1/3, 5/6 и так далее.
- Конечные десятичные дроби. Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.
Свойства рациональных чисел
- А + В = В + А
- А + (В + С) = (А + В) + С
- А + 0 = А
- А + (-А) = 0
- А * В = В * А
- А * 1 = А
- А * 0 = 0
- (А + В) * С = А * С + В * С
- (А – В) * С = А * С – В * С