Что называется осевой симметрией. Что такое ось симметрии?

• P – это точка пересечения MM₁и прямой a;
• Q – это точка пересечения NN₁и прямой a;
• построим отрезок MK, перпендикулярный NN₁;
• тогда точка K отразится в точку K₁.

Осевая и центральная симметрии. Проводим урок с ЭФУ

Мы хотим узнать, как провести урок в 6 классе об осевой и центральной симметрии с помощью ЭСП.

1. Зайдите на бесплатный сервис «Классная работа» от LECTA. В помощь учителю на сервисе «Классная работа» представлены поурочные планы по математике — календарно-тематическое планирование и методические рекомендации к каждому этапу урока. Поурочные разработки по математике содержат интерактивные материалы для изучения каждой темы и интерактивные задания для каждого урока, математические диктанты и проверочные работы для организации проверки знаний.
2. Откройте ЭФУ «Математика. 6 класс» (УМК А.Г. Мерзляка). Нужная нам тема рассматривается в параграфе 44.
3. Откройте в сервисе «Классная работа» поурочные разработки к этому учебнику. Тема «Осевая и центральная симметрии» рассматривается на трех занятиях — 127-129. Планы данных уроков вы можете скачать в этой статье, ко всем остальным занятием — по ссылке выше.

Повторение материала

На уроках математики в 5 классе учащиеся уже узнали, как выглядят фигуры с осями симметрии и как они строятся. Перед изучением осевых и центральных симметрий полезно просмотреть материал 5-го класса. Следует объяснить учащимся, что во многих случаях можно построить фигуру по положению ключевых точек.

Учитель: Отрезок можно определить по положению его ребер, треугольник — по положению его вершин. Какие еще примеры вы можете привести? Студенты: Квадрат с четырьмя точками. Ромб. Правильно. Чтобы построить фигуру, симметричную нашему треугольнику или ромбу, нужно зеркально отразить его основные точки.

Чтобы укрепить это интуитивное понимание, учитель может предложить детям сложить лист бумаги, на котором изображены симметричные фигуры.

.

Понятие симметрии

Слово «симметрия» происходит от греческого symmetria, что означает пропорциональность. В нашем случае симметрия — это свойство геометрических фигур, которое необходимо представить.

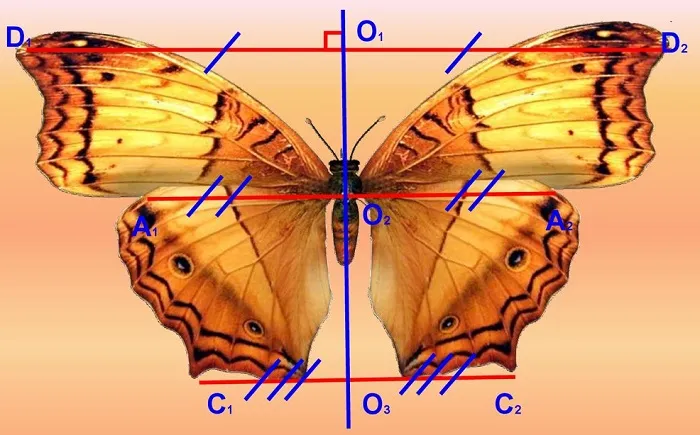
Учитель: Симметрия использовалась в рисунках, орнаментах и архитектуре с древних времен. Где еще вы можете использовать симметрию? Ученик: В строительстве домов; в изготовлении предметов быта. Учитель: Верно, но симметрия используется не только там, где люди что-то создали! В природе мы каждый день видим симметричные объекты. Назовите три таких объекта! Студенты: Бабочка, цветы, форма листа! Морская звезда, снежинка, снежинка, разрезанное яблоко.

Существует множество симметрий, какими бы странными они вам ни казались, но мы рассмотрим две симметрии на плоскости: относительно точки и относительно прямой.

Свойства осевой симметрии

1. Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
2. Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
3. Обратное преобразование осевой симметрии есть та же осевая симметрия.
4. Осевая симметрия – это поворот относительно оси симметрии на 180°.

Осевая симметрия — это движение, что означает, что при преобразовании осевой симметрии расстояние между точками сохраняется.

Если отрезок MN симметричен прямой M₁N₁относительно прямой a, тогда MN = M₁N₁.

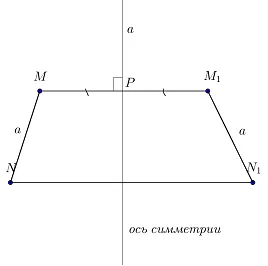
Чтобы доказать, что MN = M₁N₁сделать дополнительную конструкцию:

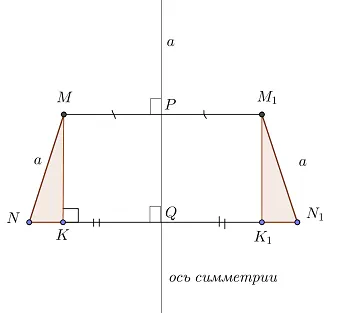
• P – это точка пересечения MM₁и прямой a;
• Q – это точка пересечения NN₁и прямой a;
• построим отрезок MK, перпендикулярный NN₁;
• тогда точка K отразится в точку K₁.

Докажите, что правильные треугольники MNK и M₁N₁K₁равны. Стороны MN и M₁N₁являются гипотенузами этих треугольников, поэтому нам нужно доказать, что перпендикуляры равны.

MK = M₁К₁поскольку они перпендикулярны параллельным прямым.

Точка N соответствует точке N₁, так что:

Поэтому треугольники равны по двум перпендикулярам так, что их гипотенузы равны, т.е. MN = M₁N₁что и требовалось доказать.

Фигуры, обладающие симметрией

Угол является осесимметричным, а его биссектриса — осью симметрии.

Из любой точки одной стороны угла опустите перпендикуляр на биссектрису угла и продлите его на другую сторону:

Рассмотрим Δ KAO и Δ MAO:

• AO – общая сторона
• Из свойства биссектрисы: ∠ MAO = ∠KAO
• Треугольники KAO и MAO прямоугольные,

Отсюда следует, что KO = OM, поэтому точки K и M симметрично касаются биссектрисы угла.

Поэтому равнобедренный треугольник также симметричен относительно биссектрисы угла, проведенной к основанию.

Равносторонний треугольник имеет три оси симметрии — биссектрисы углов, медианы и высоты отдельных углов:

Прямоугольник имеет две оси симметрии. Они проходят через центр каждой из противоположных сторон.

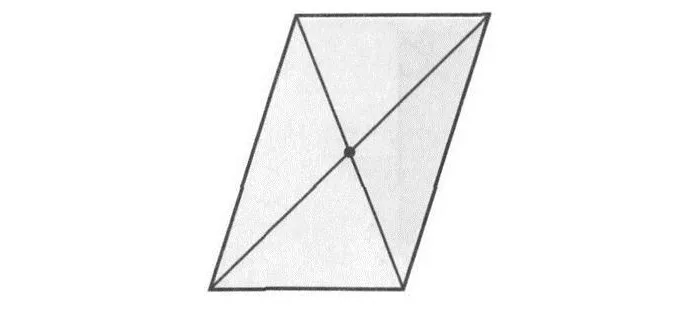
Ромб имеет две оси симметрии — это линии, которые содержат его диагонали.

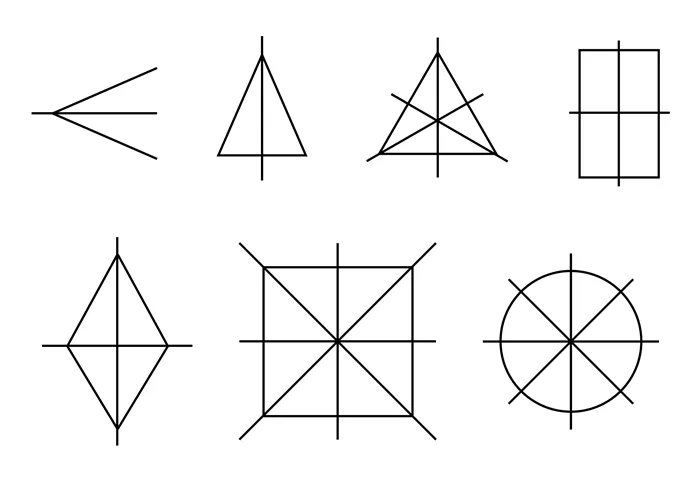
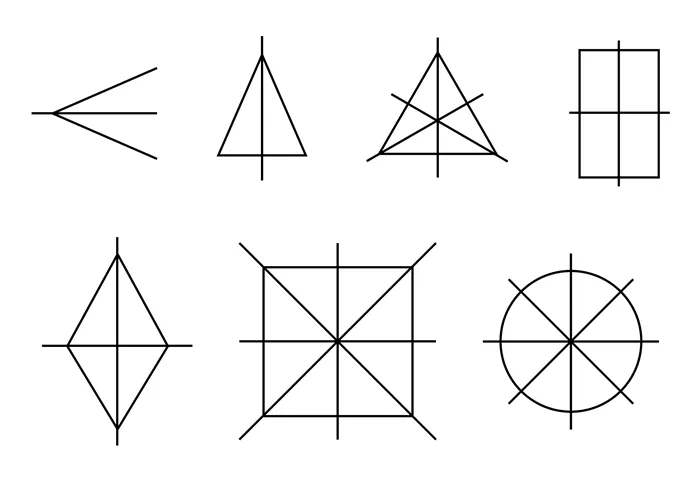
Квадрат имеет 4 оси симметрии, потому что он одновременно является ромбом и прямоугольником.

Круг имеет бесконечное число осей симметрии — это все прямые линии, проходящие через центр круга.

Симметрия в повседневной жизни

Симметрия была частью жизни человека с древних времен. Декоративные знаки зеркального отражения можно найти в древних зданиях и на древнегреческих вазах. Свойство пропорционального расположения было заимствовано наукой у природы.

Отражения часто встречаются в живой и неживой природе. Снежинки обладают этим свойством. В растительном мире противоположные элементы растений расположены одинаково: Большинство листьев являются зеркальным отражением центрального стебля. В животном царстве законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны имеют соединенные части тела: Уши, ноги, глаза, крылья, рога. Бабочка — впечатляющий пример зеркальной симметрии. Ось симметрии — это прямая линия, которая обычно проходит по середине тела насекомого.

Поскольку люди являются частью природы, они используют принцип симметрии в своих творениях. В искусстве свойство отражения используется для создания красоты и гармонии. В архитектуре пропорциональность имеет практическую функцию — она придает зданиям стабильность и надежность. В повседневных предметах единообразие проявляется в расположении фрагментов рисунка на коврах, в принтах на тканях, в узорах обоев.

Стремление к симметрии, вероятно, связано с земным притяжением. Люди интуитивно считают, что симметрия — это формула стабильности. Принцип отражения в зеркале играет важную роль в жизни человека. Стремление к гармонии и красоте заставляет людей соблюдать правила пропорциональности.

Насколько полезной была статья для вас?

Видео

Это явление в некотором смысле актуально. Она представляет собой преобразование нескольких точек пространства или области, в которых центр всегда фиксирован и не меняет своего положения.

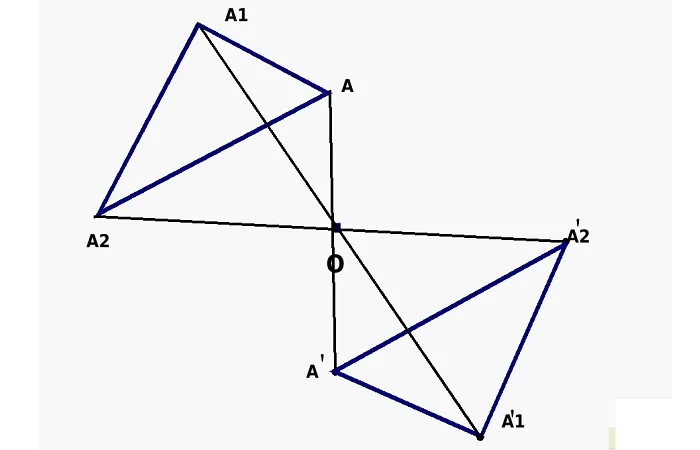
Этот тип симметрии предполагает, что два объекта, например, две точки, равноудалены от своего центра. Если провести между ними условную линию, то они расположатся на своих противоположных концах, а середина этой линии и будет осевой средней точкой.

Если предположить, что средняя точка фиксирована, и начать преобразовывать линию (т.е. вращать ее относительно средней точки), то точки на их концах описывают две кривые. Все точки на одной кривой имеют такие же симметричные точки на другой кривой.

Объекты, имеющие центр симметрии, представляют большой интерес для ученых. В геометрии существует несколько таких объектов. К ним относятся линии, отрезки, круги, прямоугольники и т.д. В природе также существуют центрально-симметричные объекты.

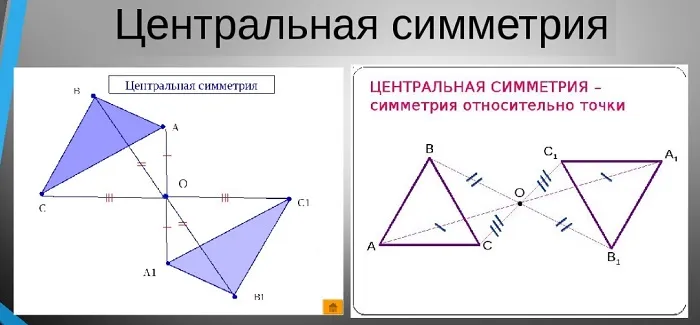
Рис. 2 Графическое представление центральной симметрии.

Фигуры, имеющие несколько осей симметрии

Существуют объекты и геометрические фигуры с определенным количеством осей. В качестве примера возьмем прямоугольник и ромб, которые имеют две такие оси.

Для прямоугольника характерны две оси симметрии. Это прямые, проходящие через точки, являющиеся серединами противоположных сторон.

Симметрия встречается в природе, в архитектуре, в мире искусства и композиции, а также в других областях человеческой жизни.

Признание этого факта прошло долгий путь, и великие умы размышляли над ним на протяжении многих веков. С древних времен до наших дней определение этого понятия прошло долгий путь.

В 8 классе геометрия посвящена симметрии: центральной, осевой, зеркальной симметрии и так далее. Чтобы не застрять во всех этих вещах, вам следует больше практиковаться. Рисуйте и наблюдайте, угадывайте симметрию и выполняйте другие упражнения. Вот несколько упражнений для тренировки. Мы верим в вас!

Задача 1. Посмотрите на симметричные геометрические рисунки и назовите тип симметрии.

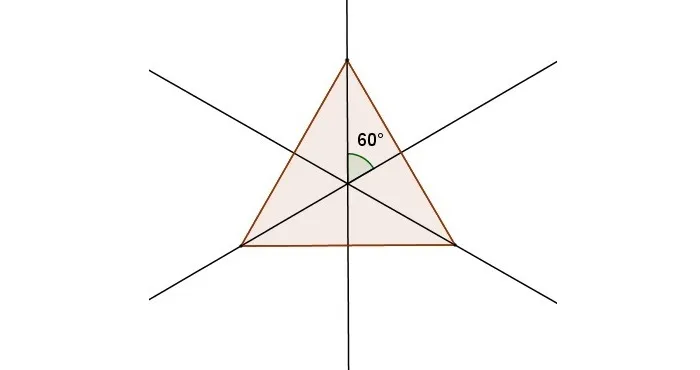
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что это так:

Симметрия относительно прямой линии — осевая Симметрия относительно точки — центральная.

Задача 2. Пусть M и N — произвольные точки, пусть l — ось симметрии. М

и N

Задачи на самопроверку

— симметричны относительно M и N относительно прямой l. Докажите, что MN = M

Примечание: Напишите перпендикуляры N

на линии ММ

Задача 3. Постройте фигуру, симметричную относительно заданной прямой a.

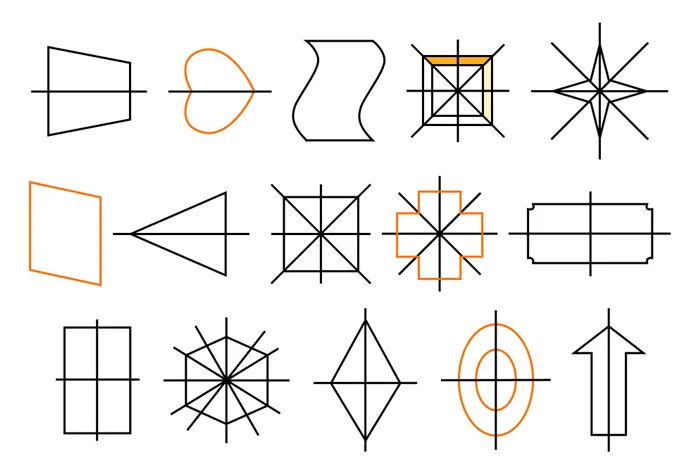
₁₁₁N₁.

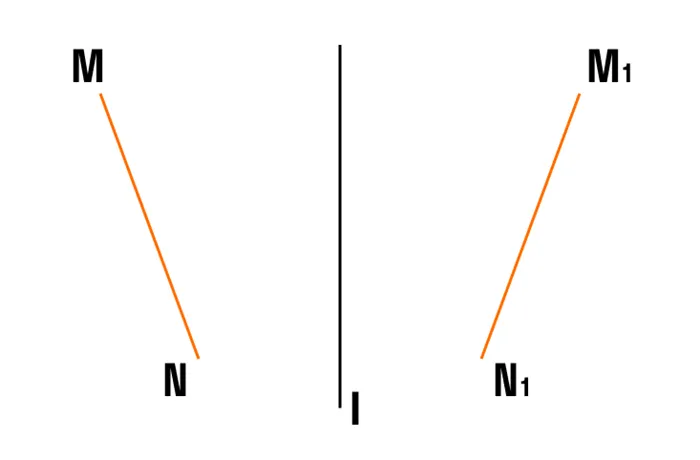
₁₁.