Только неправильные дроби имеют целую часть. Помните, что неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и их целая часть выделена:
Дроби
Дроби — это предмет, на котором спотыкается половина населения Земли. Если спросить людей, по какому предмету у них возникают проблемы с математикой, большинство из них ответят, что с дробями.
Вы не можете их винить. Дроби — это настоящий вызов. Она требует большого терпения и внимания, особенно если вы осваиваете ее впервые.
Но есть и хорошие новости. Если вы наберетесь терпения и освоите дроби, то можете быть уверены, что дальнейшее изучение математики будет легким и интересным.
И если вы хорошо усвоили предыдущий урок по дробям, то можете быть уверены, что вы уже на полпути.
Что такое дробь?
Проще говоря, дробь — это часть чего-либо. Это может быть что угодно — еда, деньги или число. Дробь называется дробью. Само слово «дробь» также говорит само за себя — дробь означает делить, разделять, делиться.
Вспомните пример из жизни. Мы купили пиццу, чтобы поесть в течение дня. Предположим, мы решили разделить его на четыре части, чтобы съесть по одному кусочку.

Посмотрите на эту фотографию. Представьте, что это наша пицца, разделенная на четыре части. Каждый кусок пиццы — это перерыв, потому что каждый кусок — это часть пиццы.
Допустим, мы съели один кусочек. Как мы можем записать его? Просто. Сначала мы проводим небольшую линию:
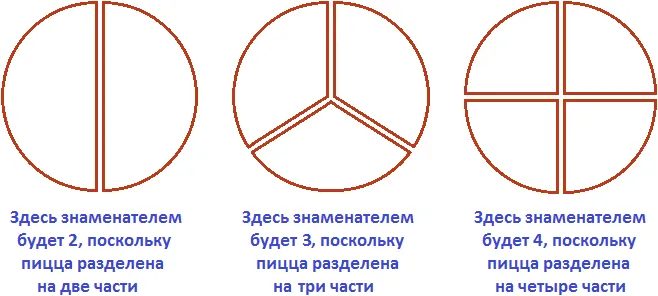
Внизу строки указано, на сколько кусочков была разделена пицца. Пицца была разделена на четыре куска. Таким образом, в конце строки вы пишете 4:
А в конце строки указано, сколько кусочков пиццы было съедено. Один кусочек был съеден, поэтому в верхней части строки мы пишем единицу:
Они называются дробями. Дробь состоит из числителя и знаменателя.
Число, которое находится вверху, является числителем дроби.
Число внизу — это знаменатель дроби.
В данном примере числитель дроби равен единице, а знаменатель дроби равен четырем. Эту дробь можно прочитать как «четверть» или «дробь от четырех» или «четверть» или «четверть», что является синонимами.
Теперь представьте, что мы съели еще один кусок той же пиццы, разделенный на четыре части. Как написать такую дробь?
Очень просто: вверху пишем 2 (потому что мы съели два ломтика), а внизу — 4 (потому что всего было четыре ломтика):
Эта дробь читается как «две четверти» или «два кусочка от четырех» или «две четверти».
Теперь представьте, что мы разделили пиццу не на четыре, а на три куска.

Предположим, мы съели один кусок этой пиццы. Как вы пишете такие
Линия в дроби, отделяющая числитель от знаменателя, означает деление. Это означает, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь. В дробной строке говорится, что четыре можно разделить на два. Мы знаем, что четыре деленное на два равно двум. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
Это самые простые примеры. Вы можете видеть, что у них нет остатка. Остальные немного сложнее, но интереснее. Мы обсудим это в следующем разделе «Разложение целой дроби».

Фракции a/b и c/d определяются как ,
Из этого определения следует, что одну и ту же дробь можно записать разными способами. Например, так как 1 — 4 = 2 — 2. Конечно, существует множество дробей, которые не являются одинаковыми. Например, da 1 — 4 ≠ 3 — 5.
Дробь означает деление
Возникает закономерный вопрос: как найти все дроби, которые равны заданной? Ответ дается в виде определения:
— Числитель и знаменатель могут быть умножены на одно и то же число, кроме нуля. Это дает дробь, которая равна заданной дроби.
Это очень важное свойство — запомните его. С помощью этого основного свойства дробей можно упрощать и сокращать многие выражения. В дальнейшем она всегда будет проявляться в виде различных свойств и теорем.
Если числитель меньше знаменателя, то дробь правильная. В противном случае, если числитель больше или хотя бы равен знаменателю, дробь ложная и в ней можно распознать целую часть.
Основное свойство дроби
Целая часть записывается перед дробью прописными буквами и выглядит следующим образом (выделено красным цветом):
Чтобы выделить целую часть неправильной дроби, необходимо выполнить три простых действия:
Насколько это может быть сложно? На первый взгляд, это может показаться сложным. Но с небольшой практикой вы сможете делать это почти устно. А пока вы можете ознакомиться с некоторыми примерами:
Работа. Обозначьте целую часть в приведенных дробях:
![]()
Во всех примерах красным цветом выделена вся часть деления, а зеленым — остальная часть деления.
Неправильные дроби. Выделение целой части
Обратите внимание на последнюю дробь, где остаток от деления равен нулю. Получается, что числитель полностью делится на знаменатель. Это имеет большой смысл, потому что 24 : 6 = 4 — это сложный факт из таблицы умножения.
Если у вас все получилось, числитель новой дроби определенно меньше знаменателя, что означает, что дробь правильная. Следует также отметить, что лучше всего записывать целочисленную часть в конце задачи перед написанием ответа. В противном случае вы можете значительно усложнить расчеты.
![]()
Существует и противоположная функция, а именно устранение
- Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди;
- Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;
- Знаменатель переписываем без изменений.
Основное свойство дробей заключается в том, что если числитель и знаменатель дроби умножить или разделить на одно и то же ненулевое число, то дробь будет равна. Формула выглядит следующим образом:
Где a, b, k — натуральные числа.
Обычная дробь и десятичная дробь — старые знакомые. Вот как они связаны между собой:
У нас есть отличные курсы математики для учеников с 1 по 11 класс, записывайтесь!
С дробями можно делать то же самое, что и с обычными числами — складывать, вычитать, умножать и делить. Их также можно использовать для сокращения и сравнения дробей. Давайте попробуем так.
Переход к неправильной дроби
Из двух дробей с одинаковым знаменателем больше та, у которой числитель больше.
Давайте сравним 1/5 и 4/5, как нам кажется:
- Умножить целую часть на знаменатель. В результате могут получаться довольно большие числа, но нас это не должно смущать;
- Прибавить полученное число к числителю исходной дроби. Результат записать в числитель неправильной дроби;
- Переписать знаменатель — опять же, без изменений.
Из двух дробей с одинаковым числителем больше та, у которой знаменатель меньше.
![]()
Сравните 1/2 и 1/8. Как рассуждать:
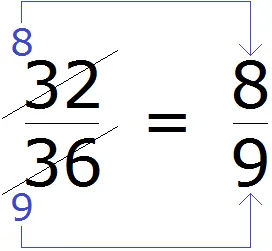
Предположим, у нас есть торт. Поскольку знаменатель первой дроби равен 2, мы делим торт на две части и берем одну часть, то есть половину торта.
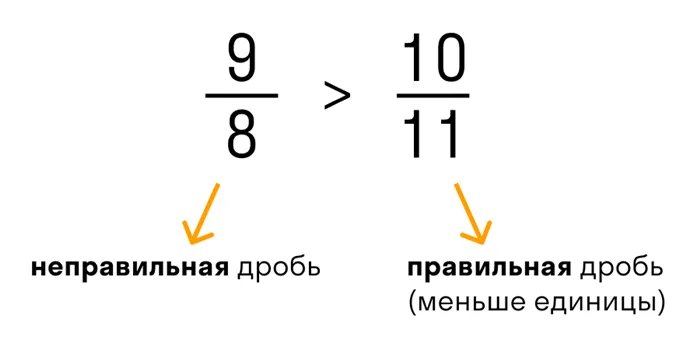
Правильная и неправильная дроби
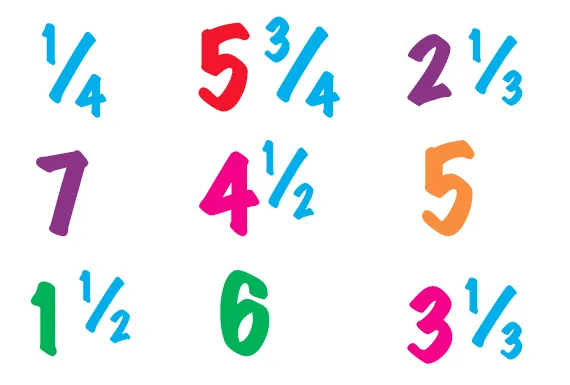
Знаменатель второй дроби равен 8, поэтому мы делим торт на восемь частей и получаем маленький кусочек. Половина торта больше, чем маленький кусочек.
1/8.
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, =\frac=\frac» width=»162″ height=»40″ />.
=\frac=\frac» width=»163″ height=»39″ />.
Чтобы сравнить дроби с разными знаменателями, нужно привести их к общему знаменателю. А когда дроби приводятся к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
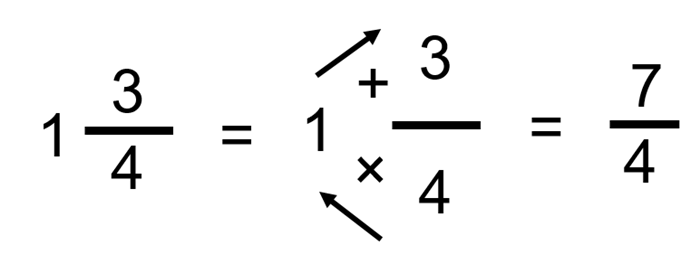
Свойства дробей
Пример. Сравните 2/7 и 1/14.
Важно помнить: любая неправильная дробь больше любой правильной дроби. Это объясняется тем, что неправильная дробь всегда больше или равна 1, а нормальная дробь всегда меньше 1.
- Дробь не имеет значения, если знаменатель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
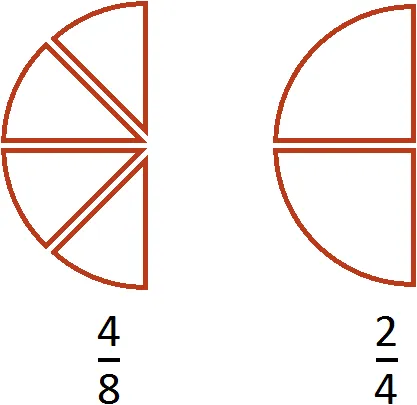
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Чтобы сравнить дроби с разными числителями и знаменателями, необходимо:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Чтобы привести дроби к общему знаменателю, необходимо:
Действия с дробями
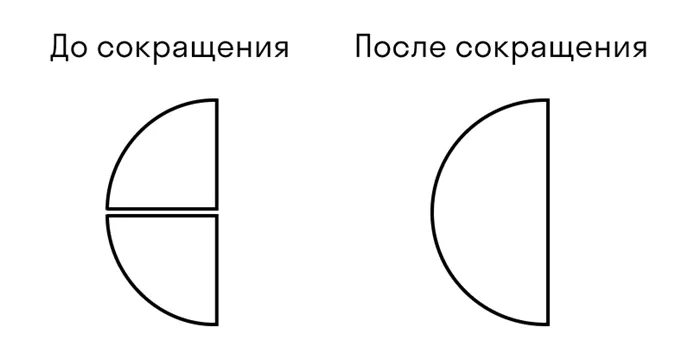
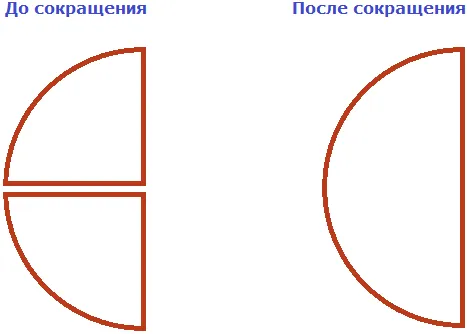
При сокращении дроби числитель и знаменатель дроби делятся на одно и то же натуральное число. Уменьшить дробь — значит сделать ее меньше и понятнее. Например, дробь 1/3 намного проще и приятнее, чем 27/81.
Сравнение дробей
Чтобы уменьшить дробь, вы удаляете числитель и знаменатель и записываете результат деления числителя и знаменателя на одно и то же число.
В этом примере две части дроби делятся на два.
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4. 1<4
- Поэтому первая дробь 1/5 меньше второй 4/5.
Вы можете не торопиться и сокращать дроби по одной в несколько этапов.
Таким образом 1/2>

- Приведем дроби к общему знаменателю:
- Сравним дроби с одинаковыми знаменателями:
- привести дроби к общему знаменателю;
- сравнить полученные дроби.
- Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей