Геометрия: свойства треугольника. Какая фигура называется треугольником?

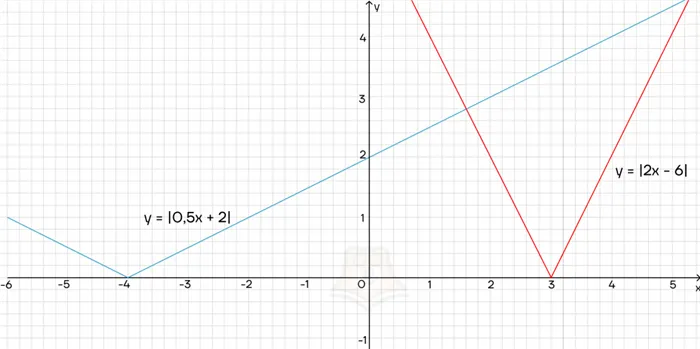
Универсальным инструментом для решения треугольников является теорема косинусов и теорема синусов. Они подходят для любого треугольника, а не только для прямых линий (как теорема Пифагора).

Треугольник

Вообще говоря, окружностей типа окружностей Веррьера, касающихся двух сторон треугольника и его описанной окружности, существует не три, а шесть: три внутренних и три внешних. Три последние касаются продолжений двух сторон треугольника и внешним образом Окружности, взаимно касающиеся друг друга внутри треугольника

• Три окружности Мальфатти попарно касаются друг друга внутри треугольника. (см. выше)
• Окружность девяти точек или окружность Эйлера касается вписанной окружности внутри треугольника в Окружности, взаимно касающиеся друг друга вне треугольника

• Три окружности Веррьера касаются описанной окружности вне треугольника.
• Окружность девяти точек или окружность Эйлера касается трех вневписанных окружностей вне треугольника внешним образом ( Файл:Circ9pnt3.svg Иллюстрация к Файл:Apollonius point.svg

Другие окружности

• Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна .

• Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, отрезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея .

Эллипсы, параболы и гиперболы треугольника

Круг (эллипс) и его перспектива

• В треугольник можно вписать бесконечно много 2 .

Окружность эллипса Штейнера и шевианты, проходящие через его фокусы.

• В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника) 3. Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера. Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера 4 .

Эллипс Брокара и точка Лемуана его перспективы

• Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит 5 .

• Файл:Inscribed parabola.png Свойства вписанной параболы

• Перспекторы вписанных в треугольник парабол лежат на описанном эллипсе Штейнера 6. Фокус вписанной параболы лежит на 7. Парабола, вписанная в треугольник, имеющая директрисой Файл:Kiepert hyperbola.png Гипербола Киперта
  • Если описанная около треугольника гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны) 8. Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек 8 .
  • Гипербола Киперта — описанная гипербола, проходящая через 9 .
  • Гипербола Енжабека — описанная гипербола, проходящая через 10

  Преобразования

  Ниже описаны три типа преобразований: 1) изогональное соединение, 2) изотомическое соединение, 3) изоциклическое преобразование.

  Фраза «Описанные окружности бесконечно удалённую прямую перейдёт описанный Изоциркулярное преобразование

  Если вписать окружности, касательные к сторонам окружности, в отрезки под окружностью, проходящие через точку, а затем соединить точки касания этих окружностей с окружностью с противоположными вершинами, то эти окружности пересекутся в точке. Составьте, расположено на тилинейной полярной окружности точки, тогда тилинейная полярная окружность точки, изогонально (изотомически) конгруэнтная точке, расположена на тилинейной полярной окружности точки).

  Кубики

  Предположим, что прямая, проходящая через эту точку, является изогонально конгруэнтным изотопическим кубом (здесь — изогонально конгруэнтная точка). Такие кубы также проходят через центры концентрической и неконцентрической окружности, а также через саму неподвижную точку и изогонально сопряжены с ней.

  • Кубика Дарбу получается, если зафиксировать точку, симметричную ортоцентру относительно центра описанной окружности. Она проходит через ортоцентр и центр описанной окружности.
  • Кубика Томсона получается, если в качестве фиксированной точки выбрать центроид. Кубика Томсона проходит через центроид, точку Лемуана, ортоцентр, центр описанной окружности, середины сторон и середины высот.
  • Кубика Мак-Кэя получится, если в качестве фиксированной точки взять центр описанной окружности. Она также проходит через ортоцентр и центр описанной окружности.
  • Кубика Нейберга — множество таких точек, что — прямой Эйлера (зафиксирована её бесконечно удалённая точка). На этой кубике лежит более 15 замечательных точек, в частности, точки Торричелли, Аполлония, ортоцентр, центр описанной окружности, вершины правильных треугольников, построенных на сторонах (внешним или внутренним образом), точки, симметричные вершинам относительно сторон, а также лежащие на всех кубиках центры вписанной и вневписанных окружностей.

  Содержание

  1. Виды треугольников
  2. Свойства сторон треугольника
  3. Свойства углов треугольника
  4. Свойства высоты треугольника
  5. Свойства медианы треугольника
  6. Свойства биссектрисы треугольника
  7. Средняя линия треугольника
  8. Равнобедренный треугольник
  9. Равносторонний треугольник
  10. Прямоугольный треугольник
  11. Треугольник и окружность
  12. Основные формулы
  13. Теорема Чевы
  14. Теорема Менелая

  

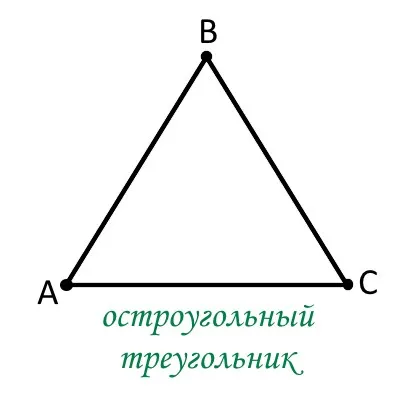
  1. Треугольник называется остроугольным, если все его углы острые.
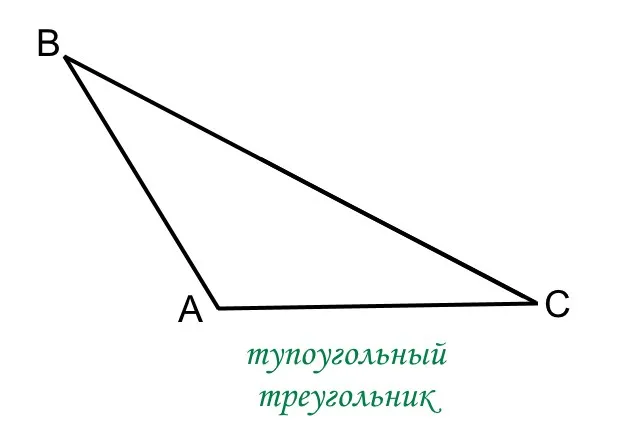
  2. Треугольник называется тупоугольным, если один из его углов тупой.
  3. Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
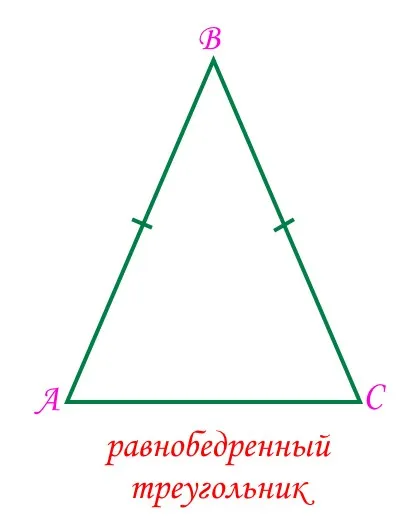
  4. Равнобедренный треугольник — треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
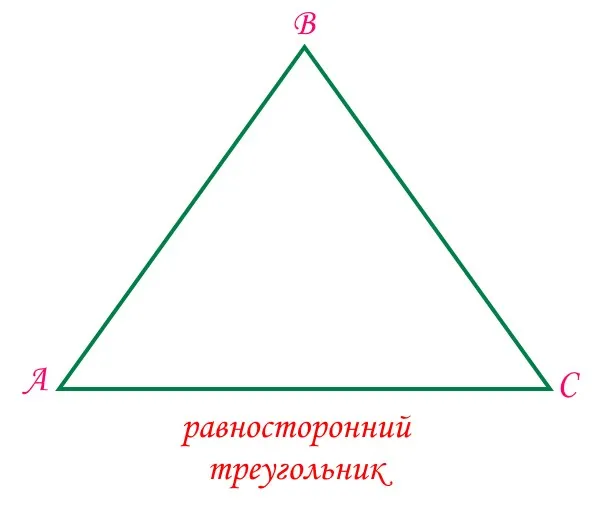
  5. Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
  6. Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны. Основные признаки равенства треугольников: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам.

  Свойства сторон треугольника

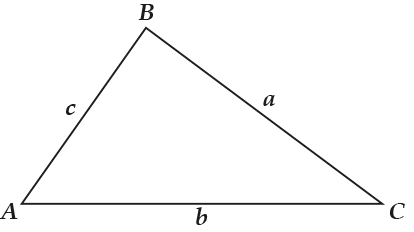
  • Сумма любых двух сторон треугольника больше его третьей стороны. На рисунке: b+c>a, a+c>b, a+b>c.
  • Длина каждой стороны треугольника больше разности длин двух других сторон. На рисунке: |a-b|
  • Сумма углов треугольника равна 180°:
  • В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
  • Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.

  Свойства высоты треугольника

  

  Высота треугольника — это перпендикуляр, проведенный из любой вершины треугольника к противоположной стороне или к продолжению стороны. На иллюстрации.

  

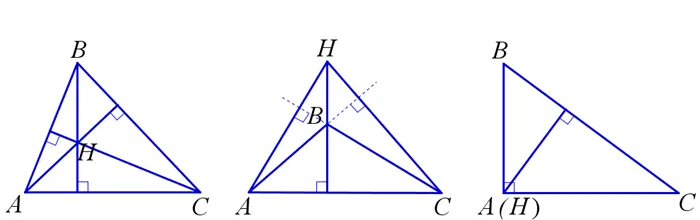
  Высоты треугольника пересекаются в точке, называемой ортоцентром треугольника. На рис: H — центр правой стороны треугольника ABC.

  Высота треугольника

  На каждом треугольнике можно нарисовать три высоты. Высота треугольника — это перпендикуляр, проведенный из вершины треугольника к стороне, противоположной вершине.

  В треугольнике, например, высота составляет.

  

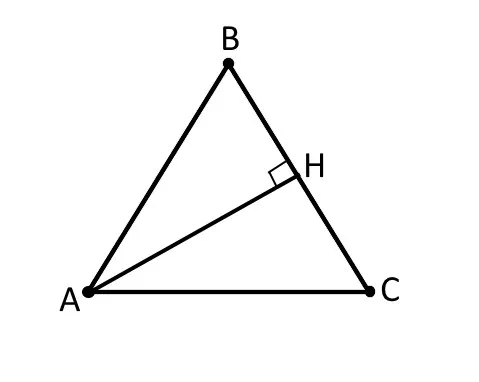
  Теперь проведите высоту от каждой вершины, чтобы получить три высоты — больше высот нарисовать нельзя.

  

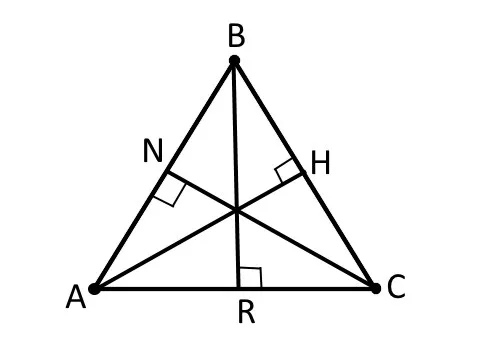
  Этот треугольник имеет три высоты, ,, , .

  О биссектрисах углов и медианах мы поговорим в других статьях. Давайте сначала разберемся, что такое треугольник.

  Виды треугольника

  Виды треугольников могут состоять из углов и сторон. То есть в первом случае вид треугольника зависит от того, какие углы содержатся в треугольнике, а во втором — от того, какие стороны содержатся в треугольнике.

  Виды треугольников по углам

  В зависимости от того, являются ли все углы треугольника острыми, есть ли тупой угол или угол равен, треугольник является остроугольным, тупоугольным или прямоугольным.

  Посмотрите на рисунки — перед вами три основных типа треугольников:

  

  

  

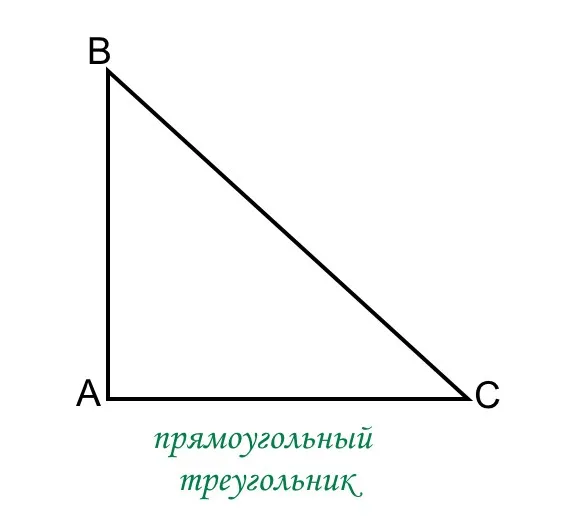
  Виды треугольников по сторонам

  Когда все стороны треугольника равны, треугольник называется равносторонним или правильным. Если только две стороны треугольника равны, он называется равнобедренным.

  На рисунке изображены равносторонний треугольник и равнобедренный треугольник.

  

  

  Свойства сторон треугольника

  Треугольник обладает важными свойствами и характеристиками.

  Устойчивость — это важное свойство треугольника, которое необходимо на уроках физики. Но сначала мы познакомимся с ним на уроках геометрии.

  Устойчивость треугольника

  Таким образом, длина третьей стороны треугольника может составлять от 4 до 10 см. В целых числах длина также может быть 5, 6, 7, 8 или 9 см.

  С помощью свойства сторон треугольника мы можем определить, существует ли треугольник с определенными сторонами.

  Чтобы проверить это, сложим длины коротких сторон, и если сумма длин будет больше длины более длинной стороны, то треугольник существует.

  Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

  Правило существования треугольника

  Решение: Проверим с помощью свойства сторон треугольника: Сложите две короткие стороны 3 и 7 см: 3+7=10, и 10

  7 — треугольник с такими длинами сторон существует.

  Следующий факт относится не к углам, а к сторонам треугольника.

  Сумма двух сторон треугольника больше его третьей стороны.

  А вот такие длины сторон 5 см, 7 см и 6 см вполне могут образовать треугольник: складываем 5+6=11 и 11>Это означает, что:

  Неравенство треугольника

  Вы уже догадались, почему этот факт называется неравенством треугольника?

  Какова теперь цель этого неравенства треугольника?

  

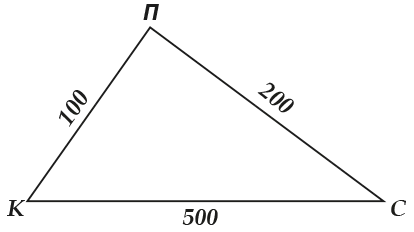
  И представьте, что у вас есть три друга: Коля, Петя и Сергей.

  Так, Коля говорит: «От моего дома до дома Пети \(100\) метров по прямой». А Петя: «От моего дома до дома Сергея — 200 метров по прямой». А Сергей: «Это тебе хорошо, а от моего дома до дома Коли 500 метров по прямой».

  Ну, тогда вы должны сказать: «Вау, вау! Один из вас говорит неправду!»

  Этого не может быть!

  Потому что если от Николая до Пети \( 100\) м, а от Пети до Сергея \( 200\) м, то расстояние от Николая до Сергея должно быть ровно меньше \( 300\) (\( =100+200\) м — иначе нарушается неравенство треугольника.

  И здравый смысл, конечно, нарушен: Каждый с детства знает, что путь до линии (\( KC/S)) должен быть короче, чем путь, начинающийся в точке \( P\) (\( K-P-C\)).

  Поэтому неравенство треугольника просто отражает этот известный факт. Теперь вы знаете, как ответить на подобный вопрос:

  

  Существует ли треугольник со сторонами \( 1,3,7\)?

  Что если существует не один, а два или более треугольников? Как вы можете проверить, одинаковые ли они? Вообще-то, по определению:

  Два треугольника равны, если они конгруэнтны, когда расположены рядом друг с другом.

  Но… это ужасно неудобное определение! Как можно разместить два треугольника даже в тетради?!

  Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: \( 1+3

  Равенство треугольников

  Но, к счастью для нас, существуют знаки равенства треугольников, которые позволяют действовать с умом, не подвергая опасности свой блокнот.

  Кроме того, открою вам секрет: для математика «положить треугольники на треугольники» означает не разрезать их и наложить друг на друга, а сказать много-много слов, доказывающих, что два треугольника совпадают, когда вы кладете их друг на друга.

  Вот почему вы никогда не должны писать в своей статье: «Я проверил — дре

  Первый признак равенства треугольников

  

  Второй признак равенства треугольников

  

  Третий признак равенства треугольников

  

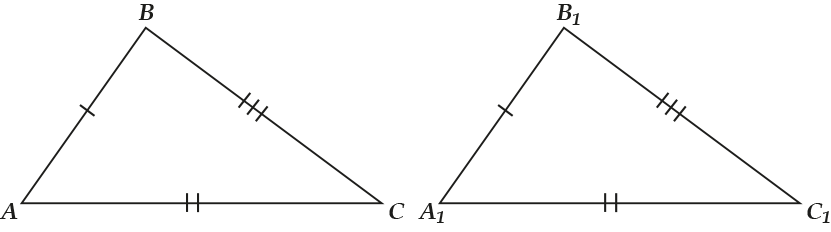
  1. Первый признак – по двум сторонам и углу между ними;
  2. Второй признак – по двум углам и прилежащей стороне;
  3. Третий признак – по трём сторонам.

  Типы треугольников (прямоугольный, равнобедренный, равносторонний) и другая теория по треугольникам

  • Равнобедренный треугольник
  • Прямоугольный треугольник
  • Равносторонний треугольник
  • Биссектриса
  • Медиана
  • Высота
  • Подобие треугольников
  • Синус, косинус, тангенс и котангенс
  • Теорема синусов
  • Теорема косинусов
    Примеры разложения многочленов на множители. Как разложить на множители?