Модуль числа. Что такое модуль в математике?

В первом случае написано условие x>0. Например, если x = 3, то числитель и знаменатель равны 3, что дает 1.

Модуль

Коэффициент числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков, минуса и плюса. В этой статье мы узнаем, что содержит число по модулю.

Мы можем легко найти расстояние от одной точки до другой, просто измерив его линейкой. Но можем ли мы найти расстояние от 0 до любого числа?

Представим, что наш дом находится на полпути между школой и магазином. Школа и магазин находятся в 500 метрах друг от друга, но они расположены на противоположной стороне дома.

Давайте поместим их на координатную линию. Поскольку школа и магазин находятся на одинаковом расстоянии, мы проходим 500 метров от дома до магазина. Но по линии координат мы проходи м-500 метров до школы, потому что идем против направления оси, и 500 метров до магазина.

В результате возникнет противоречие? Нет, потому что когда мы ищем расстояние, нас не волнует ни направление, ни отметка. В математике существует специальное определение для модуля или абсолютного значения.

Модуль — это расстояние между любой точкой на координатной прямой и началом координат.

Поскольку мы можем отложить расстояние на координатной прямой в двух направлениях, это расстояние может быть найдено как с отрицательными, так и с положительными точками. Расстояние измеряет длину отрезка, т.е. оно всегда положительно.

Можно сказать, что модуль берет только цифры из каждого числа и игнорирует знаки. Например, |-8| = 8 и |8| = 8.

Возникает вопрос: куда исчезает минус? Чтобы избавиться от минуса, просто умножьте число н а-1: (-8) * (-1) = 8. Таким образом, модуль просто умножает число н а-1.

Таким образом, модуль числа a является выражением:

Возьмем два случая: a = 8 и a = -8. Для первого |8| = 8, для второго |-8| = -(-8) = 8, поэтому определение справедливо.

Можете ли вы найти коэффициент функции? Да. Модулем любой функции является выражение:

Свойства модуля

Модуль, как и все термины в математике, имеет свои свойства.

Свойство 1. |a|>= 0.

Как уже упоминалось, модуль всегда является положительным числом, поскольку он игнорирует знак числа.

Свойство 2. |a| = |-a|.

Это свойство также подтверждает приведенный выше аргумент. Молекулы противоположных чисел, т.е. чисел с разными знаками, равны.

Свойство 3. |a|>= a.

Если число а будет положительным, например, 5, то неравенство |5|>= 5 \(\rightarrow\) 5>= 5 верно, так как знак неравенства не является строгим.

Если число а будет отрицательным, например, -5, то неравенство |-5|>= -5 \(\rightarrow\) 5>= -5 верно, потому что положительное число всегда больше отрицательного.

Свойство 4. |a * b| = |a| * |b|.

Пусть a = 5, b = -2, тогда |5 * (-2)| = |-10| = 10, а |5| * |-2| = 5 * 2 = 10, т.е. выражения равны друг другу.

Обоснование такое же, как и для предыдущего свойства. Пусть a = 10, b = -5<|10|><|-5|>Поскольку и модуль, и квадрат числа дают положительный результат, квадрат модуля можно заменить квадратом числа.

Как построить график функции с модулем? Во-первых, давайте разберемся, что делает модуль при построении графика функции.

Рассмотрим функцию y = x — прямая линия. Y может быть как положительным, так и отрицательным.

Поставим x под знак модуля: y = |x|. Теперь y может быть только положительным. Что произойдет с частью диаграммы под осью x? Она зеркально отражена. В конце мы ставим галочку:<3.

Модуль зеркально отражает каждый график относительно оси x.

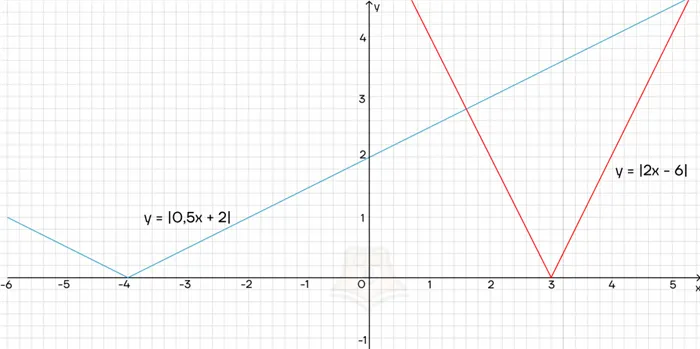
Что произойдет, если перед осью x будет модуль? Давайте построим графики:₀Клещ будет сужаться и расширяться. Чем больше коэффициент перед x, тем более узкой будет рамка.

Из уравнения x = a, из-за ограничений на x получаем a>Давайте попробуем добавить сумму к выражению субъединицы.

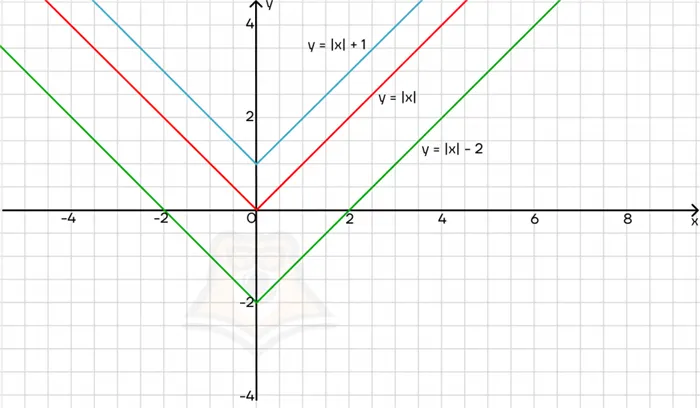
График коэффициента перемещается вдоль оси x. Также:<0.

Мы добавляем число к коэффициенту, а не к субмерному выражению:

График перемещается вдоль оси y.

Вам нужно только добавить знак минус перед коэффициентом. Важно поставить знак минус перед единицей, а не в единице. В этом случае график является зеркальным отражением оси x и лежит непосредственно под ней.

График модуля

В переводе с латинского «modulus» означает меру, размер.

Считается, что этот термин был впервые введен английским философом и математиком Роджером Коутсом, другом и учеником Исаака Ньютона.

Многие ученые использовали термин коэффициент в своих научных статьях, но только в конце 19 века ему было дано символическое название.

В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символическое обозначение коэффициента числа, которое используется и сегодня.

В некоторых случаях «мера числа» заменяется «абсолютной величиной», но важно знать, что это эквивалентные термины.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна для зарегистрированных пользователей

если мы прибавляем число, то график сдвигается влево;
если мы вычитаем число, то график сдвигается вправо.

В математике термин «единица» имеет несколько значений. Давайте проанализируем, что в математике называется модулем числа (абсолютной величиной).

Геометрия: свойства треугольника. Какая фигура называется треугольником?

Модуль числа (абсолютная величина)

Эта информация доступна зарегистрированным пользователям

Рассмотрим понятие единства с геометрической точки зрения.

Вы уже знаете, что мы отмечаем действительные числа на координатной прямой и что каждому действительному числу на этой прямой соответствует определенная точка, и наоборот, каждой точке на координатной прямой соответствует действительное число.

Точка определяется определенным расстоянием от начала координат.

Длина отрезка от начала координат до точки соответствует определенному количеству единичных отрезков координатной прямой.

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Длина такого отрезка всегда является неотрицательной величиной.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Единицей измерения координатной линии является 1 деление — 1 метр.

Теперь отложите координату первого шарика A (+ 4 ) вправо.

Теперь рассмотрим некоторые свойства коэффициента числа.

1. мера нуля равна нулю

Поскольку не существует расстояния от нуля до начала координат (0 частей единицы), мера нуля равна нулю.

|0| = 0

2. модуль числа всегда неотрицательное число (т.е. положительное или нулевое).

Длина такого отрезка всегда является неотрицательной величиной.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Эта информация доступна для зарегистрированных пользователей

Свойства модуля (абсолютной величины)

Точка O на координатной прямой — это точка, из которой шар покатился — начальная точка.

Один отрезок прямой линии равен 1 делению — 1 метру.

Точка A на координатной прямой A (+ 3 ) — это момент удара мяча о стену.

Точка B с координатой B ( 0 ) — совпадает с начальной точкой.

Можно ли сказать, что мяч не прошел никакого расстояния, пока покоился в начале координат, потому что он приземлился в точке 0 м (ни один единичный отрезок не подходит от точки 0 до начала координат O)? Конечно, нет!

Шарик прошел бы путь, равный нулю, если бы его вообще не толкали и он оставался бы в состоянии покоя в точке O.

Однако следует учитывать, что путь (расстояние), пройденный мячом, состоит из 3 единичных отрезков справа и 3 единичных отрезков слева; если мы все

Длина такого отрезка всегда является неотрицательной величиной.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Проблема 1.

Решение:

Проведем координатную линию с началом координат в точке O.

Эта информация доступна для зарегистрированных пользователей

Мы знаем, что мерой числа является расстояние (количество единичных отрезков) от нуля до данной точки.

Мы можем отложить 142 единичных отрезка вправо на координатной прямой и получить точку с координатами 142.

Мы также можем отложить 142 единичных отрезка влево от нуля и получить точку с координатами 142.

На координатной прямой есть два числа, которые по модулю равны 142, и расстояние между этими точками содержит по 142 единичных отрезка.

|142| = 142

Длина такого отрезка всегда является неотрицательной величиной.

Что называется осевой симметрией. Что такое ось симметрии?

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите числа — 15 ; — 1 ; — 1 ? 4 ; 7 в порядке возрастания по модулю.

Решение задач с применением модуля числа

Решение:

Следует понимать, что мы не располагаем числа — 15 ; — 1 ; в порядке возрастания. 4 ; 7, но их модули.

Для этого мы должны определить модули каждого из них:

|-15| = 15

|-1| = 1

Длина такого отрезка всегда является неотрицательной величиной.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите эти числа в порядке возрастания (от наименьшего к наибольшему):

1, 4, 7, 15 .

Это дает следующую последовательность уравнений,

|-1| = 1

|4| = 4

|7| = 7

|-15| = 15

Следовательно, числа должны располагаться в порядке возрастания их модуля: -1, 4, 7, 7, -15

Ответ: — 1, 4, 4, 7, 7, — 15

|-15| = 15

На координатной прямой мы отметили две точк и-73 и 68. Какой коэффициент числа больше?

Решение:

Представьте, что на координатной прямой на определенном расстоянии от точки O (начало координат) отмечены две точки.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Понятие модуля числа часто кажется студентам пугающим и непонятным. На самом деле, в этой теме по математике 6 класса нет ничего сложного. Чтобы лучше понять вопрос, давайте рассмотрим основные моменты, связанные с понятием коэффициента.

Мы начнем с понятия числовой линии и вектора. Прямая линия — это линия, на которой можно увидеть направление движения, точку 0 (начало координат) и величину единичного перехвата.

Каждое из действительных чисел может быть отмечено на числовой прямой. Независимо от подмножества, размер числа и его десятичные знаки. Прямая линия бесконечна и поэтому подходит абсолютно ко всем числам, кроме комплексных.

Числовая линия часто используется для сравнения различных типов чисел. Если отметить на линии два числа, то число справа будет больше, а число слева — меньше.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Модуль — это размер сегмента вектора. То есть, если число обозначено символом модуля, то вычитается параметр направления вектора. В геометрии это необходимо для нахождения сумм векторов и вообще для любых алгебраических операций с векторами. В этом примере невозможно указать и учесть направление, поэтому был придуман модуль.

В алгебре модуль числа означает, что при вычислениях учитывается только размер отрезка, без учета направления. На практике это означает, что

повороты модуля:

Возникает вопрос, почему отрицательное число становится положительным? Знак минус указывает только направление вектора. Символ знака минус указывает направление знака. А знак модуля отменяет параметр направления. Может ли размер сегмента быть отрицательным? Нет, конечно, нет. Таким образом, коэффициент отрицательного числа всегда является положительным числом.

|-15| = 15

В этом уроке мы более подробно рассмотрим понятие коэффициента числа.

Модуль — это расстояние между началом координат и числом на координатной прямой. Поскольку расстояние никогда не бывает отрицательным, модуль всегда неотрицателен. Поэтому модуль числа 3 равен 3, так же как модуль числ а-3 равен 3.

Предположим, что на координатной прямой расстояние между целыми числами равно одному шагу. Если теперь обозначить числ а-3 и 3, то их расстояние от начала координат равно трем шагам:

Коэффициент — это не только расстояние между началом координат и числом. Модулем также является расстояние между любыми двумя числами на координатной прямой. Это расстояние выражается как разность между этими числами с помощью символа модуло:

Модуль числа

Где x

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Числовая прямая

и х

— это числа на координатной прямой.

Например, отметьте на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью коэффициента. Для этого напишите разность между числами 2

В зависимости от того, что подставляется вместо x, выражение | x | равно x, если подставляемое число больше или равно нулю. А если x заменить на число, меньшее нуля, то выражение | x | будет равно — x .

Модуль

Второй случай на первый взгляд может показаться противоречивым, поскольку обозначение | x | = — x выглядит так, как будто модуль становится равным отрицательному числу. Если x равно 0, то под символом модуля стоит отрицательное число. После знака равенства замените x на это отрицательное число и раскройте скобки.Например, найдите коэффициен т-7, используя правило разложения по модулю:

Положительное число и вектор, сонаправленный с числовой прямой.
Отрицательное число и вектор, направленный в противоположную числовой прямой сторону.
Число ноль или ноль-вектор – это вектора без направления.

В этом случае второе условие для x имеет вид

Поэтому мы используем вторую формулу. То есть, | x | = — x. Вместо x мы добавляе м-7.Пример 2: Пусть x = 5. То есть, мы рассматриваем коэффициент 5.

Положительное число в положительное.
Отрицательное число в положительное.
Ноль в ноль.

Ломаная линия. Какая фигура называется ломаной?

В этом случае первое условие x ≥ 0 выполняется, так как 5 ≥ 0.

Поэтому мы используем первую формулу. То есть | x | = x. Получаем | 5 | = 5.

Обобщённое понятие модуля числа

Нулевая точка — это своего рода точка перехода, в которой модуль меняет порядок расширения, а затем сохраняет свой знак. Визуально это можно представить следующим образом:

На рисунке красные символы минус и плюс показывают, как модуль | x | изменяется в интервалах x

Например, если взять числа 1, 9 и 13, которые принадлежат интервалу x ≥ 0, то модуль | x | расширяется со знаком плюс в соответствии с рисунком:

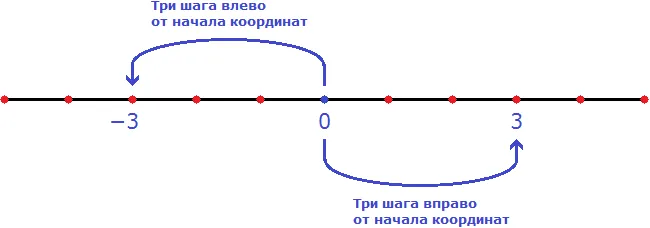
А если взять числа меньше нуля, например, -3, -9, -15, то модуль раскладывается со знаком минус в соответствии с рисунком:

Пример 3: Пусть x = √4 — 6. То есть, рассмотрим коэффициент выражения √4 — 6,₁Квадратный корень из 4 равен 2. Тогда коэффициент равен₂x, который был √4 — 6, теперь становитс я-4. В этом случае второе условие x.

Коэффициент выражения можно рассматривать как полный множитель. Его можно сократить и вывести за скобки. Если модуль является частью многочлена, его можно добавить к аналогичному модулю.

Как и обычный буквенный множитель, модуль имеет коэффициент. Например, модуль модуля | x | равен 1, а модуль модуля -| x | раве н-1. Модуль модуля 3| x +1| равен 3, а модуль модул я-3| x +1| раве н-3.

Пример 1. Упростите выражение | x | + 2| x | — 2 x + 5 y и укажите коэффициент полученного выражения.

Решение

Выражения| x | и 2| x | являются аналогичными понятиями. Запишите их. Остальное оставьте без изменений:

Расшифруйте коэффициент выражения. Если x ≥ 0, то имеем 3 x — 2 x + 5 y, где x + 5 — y.

Когда х₁мы имеем следующее решение:₂Пример 2: Разложите по модулю выражение: -| x |₂мы имеем следующее решение:₁.

Раскрытие модуля

В этом случае символу модуля предшествует знак минус. Его можно понимать как минус один перед символом модуля. Если x ≥ 0, модуль приобретается со знаком плюс.

Например, если знак абсолютного значения содержит математическое выражение, вы должны рассмотреть применимые математические определения, прежде чем раскрывать коэффициент.

|A + 5| = A + 5, если A больше или равно нулю.

5-A, если A меньше нуля.

В некоторых случаях знак может быть однозначно определен для любого значения переменной.

Рассмотрим другой пример. Построим координатную линию, на которой отметим все числовые значения, абсолютная величина которых равна 5.

Сначала необходимо провести координатную линию, отметить на ней начало координат и определить размер единичного отрезка. Линия также должна иметь направление. Теперь на этой линии нужно нарисовать метку, соответствующую размеру единичного отрезка.<0, ведь −7<0

Итак, мы видим, что на этой координатной прямой есть две интересующие нас точки со значениями 5 и-5.

<0 и x ≥ 0 .

<0, ведь −4<0

Преобразование выражений с модулями

<0, то получим − 3 x − 2 x + 5 y, откуда − 5 x + 5 y. Вынесем за скобки множитель − 5, получим − 5( x − y )

Геометрическое значение

Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.

Свойства абсолютной величины

Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>0 .
Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а| .
Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0| .
Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В| .
Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | | .
Такое же правило распространяется и на показатель степени выражения.

Модуль числа. Что такое модуль в математике?

Модуль

Свойства модуля

График модуля

Модуль числа (абсолютная величина)

Свойства модуля (абсолютной величины)

Решение задач с применением модуля числа

Модуль числа

Числовая прямая

Модуль

Обобщённое понятие модуля числа

Раскрытие модуля

Преобразование выражений с модулями

Геометрическое значение

Свойства абсолютной величины

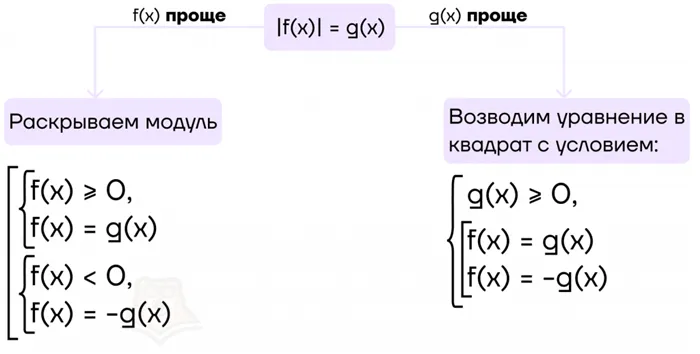
Особенности решения уравнений с модулем