Признаки равенства треугольников. Как доказать что треугольники равны?

Если две стороны и угол между ними треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Теоремы за 7 класс по геометрии

Прежде чем приступить к доказательству теоремы, необходимо вспомнить, что такое треугольник и в каком случае два треугольника можно считать равными.

Что такое треугольник и когда они считаются равными?

Треугольник — это геометрическая фигура, состоящая из трех отрезков, соединяющих три точки (если они не лежат на одной прямой). Эти точки считаются вершинами треугольника. А отрезки, которые их соединяют, являются сторонами).

На рисунке 1 изображен треугольник ABC. который имеет три вершины (A, B и C). А стороны равны AB, AC и BC.

Треугольники считаются равными, если все их стороны и углы равны (если равны только углы, а стороны пропорциональны, треугольники называются сопряженными). Таким образом, очевидно, что равные треугольники можно положить друг на друга — и они будут полностью совпадать.

Доказательство первого доказательства равенства треугольников

Два треугольника: ABC и DEF (рис. 2).

Согласно теореме, две пары отрезков этих треугольников равны между собой (AC = FD и CB = EF). Углы между отрезками также равны (т.е. ∠ ABC = ∠ EFD).

Докажите, что треугольник ABC равен треугольнику DEF.

Доказательство:

1. поскольку углы равны (∠ ABC = ∠ EFD), треугольники можно расположить так, чтобы вершина C совпадала с вершиной F.

(2) Отрезки CA и CB пересекаются с отрезками FE и FD.

(3) Поскольку отрезки двух треугольников одинакового размера (AC = FD и CB = EF), отрезок AB также совпадет со стороной ED.

(4) Это, в свою очередь, приводит к совпадению вершин A и D, B и E.

5. следовательно, треугольники полностью конгруэнтны, т.е. равны.

Теорема доказана.

Второе доказательство равенства треугольников

Если одна сторона и два смежных угла треугольника равны одной стороне и двум смежным углам другого треугольника, то эти треугольники равны.

MN = PR ∡ N = ∡ R ∡ M = ∡ P

Как и в случае с доказательством первого пункта, нам нужно проверить, достаточно ли этого для того, чтобы треугольники были равны, могут ли они быть полностью конгруэнтными?

(1) Поскольку MN = PR, эти отрезки конгруэнтны, если их конечные точки совпадают.

2 Поскольку ∡ N = ∡ R и ∡ M = ∡ P, MK и NK накладываются на PT и RT соответственно.

3 Если лучи совпадают, то их пересечения K и T также совпадают.

4 Все вершины треугольников конгруэнтны, т.е. Δ MNK и Δ PRT полностью совпадают, т.е. равны.

Третья точка равенства треугольников

Если три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники равны.

ПН = ПНКН = ТРМК = ПТ

Давайте снова попробуем расположить треугольники Δ MNK и Δ PRT и обнаружим, что соответствующие равные стороны и соответствующие углы этих треугольников равны и полностью совпадают.

Например.

1. если две параллельные прямые пересекаются вторичной прямой, то углы пересечения равны.

2. если две параллельные прямые пересекаются вторичной прямой, то соответствующие углы равны. 3.

Теорема об углах, образованных двумя параллельными прямыми и секущей

3. если две параллельные прямые пересекаются вторичной прямой, то сумма односторонних углов равна 180°. 4.

4. если точки пересечения двух прямых из точки пересечения вторичной прямой равны, то прямые параллельны.

1. Предположим, что параллельные прямые a и b пересекаются малой линией MN ( c ). Докажите, что углы пересечения 3 и 6 равны. Предположим, что углы 3 и 6 не равны. Определите угол PMN, который равен углу 6 MN, так что PMN и угол 6 являются углами пересечения MP и b MN. По построению, эти углы пересечения равны, т.е. MP || b. Предположим, что существуют две прямые (прямые a и MP ), которые проходят через точку M и параллельны прямой b. Однако это противоречит аксиоме о параллельных прямых. Следовательно, наша гипотеза неверна и угол 3 равен углу 6.

3.4 Углы с параллельными или прямыми сторонами

Если стороны угла параллельны сторонам другого угла, то эти углы равны или общие.

Доказательство

(соответствующие параллельному и вторичному ). (соответственно параллельные и вторичные ). (перпендикуляр), поэтому. = и = (по свойству смежных углов). Эти два уравнения остаются верными, если мы заменим. на равный угол. Тогда = и = — это то, что нужно было доказать.

Если стороны одного угла перпендикулярны сторонам другого угла, то эти углы равны или вместе дают величину .

= — и = -, таким образом. || и ||. (согласно Теореме 1). Из этого следует. Тогда, =, = .

Два треугольника считаются равными, если все их соответствующие стороны и все соответствующие углы равны.

Существуют следующие основные положения равенства треугольников:

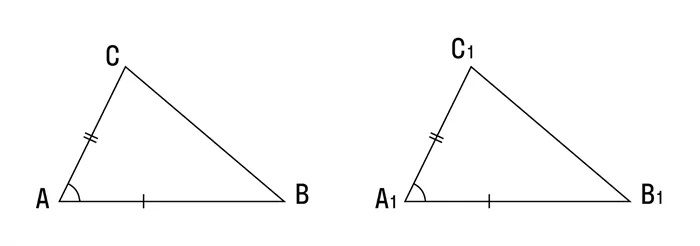
Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны. На рис: AB=A1B1, AC=A1C1, ∠BAC=∠B1A1C1 ⇒ △ABC=△A1B1C1.

Признаки равенства треугольников

Если одна сторона и два смежных угла треугольника равны одной стороне и двум смежным углам другого треугольника, то эти треугольники равны. На рис.

Если три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники равны. На рис: AB=A1B1, AC=A1C1, BC=B1C1 ⇒ △ABC=△A1B1C1.

1. По двум сторонам и углу между ними,
2. По стороне и двум прилежащим к ней углам
3. По трем сторонам.

Первый признак равенства треугольников

Три точки равенства треугольников являются фундаментальными. Но есть и другие признаки, о которых следует помнить.

1. если угол, сторона, касательная к этому углу, и высота, данная на другой стороне одного треугольника, равны углу, стороне и высоте другого треугольника соответственно, то эти треугольники равны.

Третья точка равенства треугольников

2. если две стороны и медиана одного треугольника и медиана между ними соответственно равны двум сторонам и медиане другого треугольника, то эти треугольники равны.

3. если одна сторона и две медианы треугольника равны стороне и двум медианам другого треугольника, то эти треугольники также равны.

4. если две стороны и биссектриса между ними одного треугольника равны двум сторонам и биссектрисе другого треугольника, то эти треугольники также равны.

5. два треугольника равны, если сторона, среднее и высота одного треугольника соответственно равны стороне, среднему и высоте другого треугольника.

Все свойства треугольника можно найти в статье: Геометрия: свойства треугольника.

Теория:

Два треугольника равны, если три стороны одного треугольника равны трем сторонам другого треугольника.

Доказательство:

Третья точка равенства треугольников

Рассмотрим два треугольника ABC и A

B

Доказательство:

Рассмотрим следующее:₁Докажите, что₁ABC = A₁B

C

Добавьте треугольники ABC и A₁Докажите, что₁ABC = A₁.

друг к другу так, чтобы вершина A была конгруэнтна с A₁Докажите, что₁ABC = A₁лежат по разные стороны от прямой AC.₁Соединение Б и В₁вы получите два равнобедренных треугольника BAB₁и БАБ

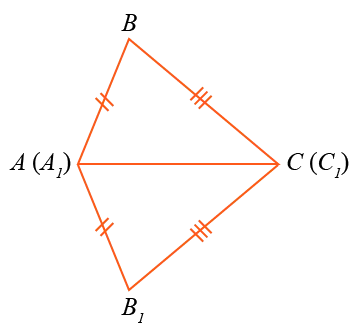
В треугольнике BAB₁∠ 1 = ∠ 4, в BAB₁∠ 2 = ∠ 3 (как угол при основании). Следовательно,₁.

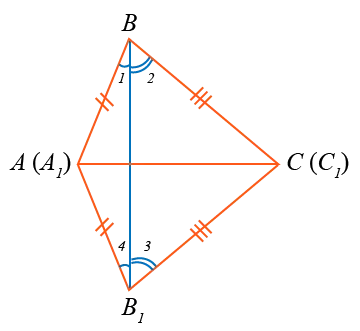
∠ 1 + ∠ 2 = ∠ 4 + ∠ 3, поэтому ∠ABC = ∠ABC₁C .₁Поэтому AB = A

B₁, BC = B

C₁Докажите, что₁B₁ABC = A₁Отсюда следует, что треугольники ABC и A₁Докажите, что₁ABC = A₁.

равны в соответствии с первой конвенцией о равенстве треугольников. Теорема доказана.₁Докажите, что₁ABC = A₁

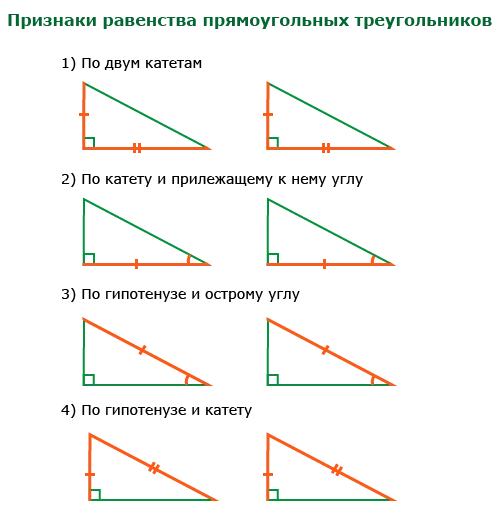
Признаки равенства прямоугольных треугольников

1. Если катеты одного треугольника равны катетам другого.
2. Если катет и прилежащий к нему острый угол одного треугольника равны катету и прилежащему к нему острому углу другого.
3. Если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
4. Если гипотенуза и катет одного треугольника равны гипотенузе и катету другого.