Сложение и вычитание дробей. Как складывать дроби с разными знаменателями?

Небольшое замечание по последним двум примерам, где дроби вычитаются с подчеркнутой целой частью. Знак минус перед второй дробью означает, что вычитается вся дробь, а не только целая часть.

Урок 12 Получить доступ за 75 баллов Сложение и вычитание дробей с разными знаменателями

В этом уроке мы рассмотрим, как складывать и вычитать обыкновенные дроби, а также научимся складывать и вычитать обыкновенные дроби и десятичные дроби.

Сначала мы рассмотрим самый простой случай, когда дроби имеют одинаковый знаменатель.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Интуитивно понятно, что если сложить \(\mathbf>\) и \(\mathbf>\), то получится \(\mathbf>\)

Действительно, это так.

Как правило, при сложении двух дробей с одинаковым знаменателем получается дробь, у которой знаменатель равен слагаемому, а числитель равен сумме числителей слагаемых.

Также нередко встречаются короткие дроби, поэтому числитель и знаменатель необходимо сократить.

Эта информация доступна зарегистрированным пользователям

Ответом будет дробь, в которой числитель такой же, как и в заданных дробях, т.е. 5 .

Запишите в числитель результата сумму числителей данных дробей, т.е. сумму 3 и 1.

В данном случае результатом является несократимая дробь, поэтому это окончательный ответ.

Также выполните алгоритм, добавив дробь со знаменателем 12 и прибавив к числителю сумму числителей исходных дробей, то есть сумму 1 и 3.

В данном случае мы имеем дело с дробью, числитель и знаменатель которой имеют общий множитель, а именно 4.

Что такое бином Ньютона и почему им всех пугают. Бином ньютона что это?

Затем нужно уменьшить дробь на это значение.

Поскольку дробь не разлагается, ответ будет таким.

Теперь перейдем к вычитанию.

Это работает и в этом случае, если знаменатели одинаковы.

Также представим, что у нас есть \(\mathbf>\) и надо вычесть \(\mathbf>\), очевидно, что результат будет равняться \(\mathbf>\).

Правило гласит: если вычесть одну дробь из другой, а знаменатели равны, то получится дробь, числитель которой равен разности числителей, а знаменатель — той же дроби.

Чтобы привести дроби к общему знаменателю, нужно привести дроби к общему знаменателю.

Сложение и вычитание дробей с разными знаменателями

Он равен коэффициенту наименьшего общего кратного и общего знаменателя.

А затем каждую из дробей нужно умножить на соответствующий ей дополнительный коэффициент.

После этих операций мы получаем две дроби с одинаковыми знаменателями и можем выполнять операции по алгоритму предыдущей части.

Давайте рассмотрим несколько примеров, чтобы понять, как это работает.

Как мы уже говорили, сначала нужно привести дроби к общему знаменателю.

Наименьшее общее кратное 2 и 3 равно 6, поэтому к первой дроби прибавляем 3 (\(\mathbf\)), ко второй — 2 (\(\mathbf\)).

Умножьте первую дробь на ее дополнительный коэффициент.

Теперь умножьте вторую дробь на ее дополнительный коэффициент.

Теперь у нас есть две дроби с одинаковым знаменателем. Сложите их, используя алгоритм сложения дробей с одинаковым знаменателем.

Снова проверяем, является ли дробь несводимой.

В данном случае это так, поэтому это и есть ответ.

Как и в прошлый раз, мы начнем с нахождения общего знаменателя.

Наименьшее общее кратное 4 и 6 равно 12.

Аддитивный коэффициент первой фракции равен 3 : \(\mathbff\).

Аддитивный коэффициент второй фракции равен 2: \(\mathbff\).

Умножьте первую дробь на ее аддитивный коэффициент:

Затем добавьте вторую дробь:

Объем параллелепипеда. Как найти объем параллелепипеда?

А затем выполните вычитание из одной дроби в другую:

Проверяем еще раз: дробь не уменьшается, значит, это и есть ответ.

Теперь давайте посмотрим, как складывать и вычитать обыкновенные дроби и десятичные дроби.

Опять же, мы добавляем еще один шаг в начале алгоритма: преобразование десятичной дроби в дробь.

Это очень просто. Давайте рассмотрим, как именно.

Сначала нужно переписать исходную дробь в новую дробь, где числитель — десятичная дробь, а знаменатель — единица:

Затем просто умножьте числитель и знаменатель на 10, пока числитель не станет больше или равен единице:

Эта информация доступна зарегистрированным пользователям

Действия между обыкновенными и десятичными дробями

Давайте рассмотрим несколько примеров.

Сначала преобразуйте десятичную дробь в обычную дробь:

Теперь нужно привести дроби к общему знаменателю.

Мы проверяем, что дробь нельзя уменьшить, и делаем вывод, что это и есть ответ.

Опять же, мы преобразуем десятичную дробь в обыкновенную дробь:

Мы намеренно не сокращаем дробь, чтобы в дальнейшем, если нам понадобится умножить дробь на 2, нам не пришлось делать лишних шагов.

Затем мы приводим дроби к общему знаменателю и считаем сумму:

Это та сумма, которая нам необходима.

Посчитайте разность \(\mathbf-0.1>\):

Приведение дробей к общему знаменателю. Как привести дробь к общему знаменателю?

Эта информация доступна для зарегистрированных пользователей

Правила сложения дробей с разными знаменателями:

Примеры сложения дробей с разными знаменателями:

Правила сложения смешанных дробей:

Пример сложения смешанных фракций:

Эта информация доступна зарегистрированным пользователям

Сложение дробей с разными знаменателями.

2. запишите дроби так, чтобы запятые находились друг под другом.

приводим дроби к наименьшему общему знаменателю (НОЗ). Для этого находим наименьшееобщее кратное (НОК) знаменателей;
складываем числители дробей, а знаменатели оставляем не меняя;
сокращаем дробь, которую получили;
если получили неправильная дробь – преобразовываем неправильную дробь в смешанную дробь.

3. сложите дроби без запятой.

Сложение смешанных чисел (смешанных дробей).

4. в сумме поставьте запятую под запятыми тех дробей, которые вы складываете.

приводим дробные части этих чисел к наименьшему общему знаменателю (НОЗ);
отдельно складываем целые части и отдельно дробные части, складываем результаты;
если при сложении дробных частей получили неправильную дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части;
сокращаем полученную дробь.

Примечание.

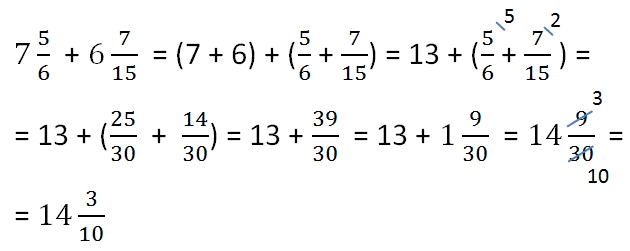
Сложение десятичных дробей.

Если данные десятичные дроби имеют разное количество десятичных знаков, то для дроби с меньшим количеством десятичных знаков мы добавляем нужное нам количество нулей, для уравнения в дробях мы добавляем количество десятичных знаков.

Рассмотрим пример. Найдите сумму десятичных знаков:

Приравняйте количество десятичных знаков к десятичным числам. Добавьте 2 нуля к правой части десятичного числа 13,7.

Если вы достаточно хорошо знаете, как складывать десятичные числа, вы можете добавить недостающие нули в уме.