Полученные формулы V и S полезны для решения различных практических задач и доказательства теорем (по рисункам). Формулы для параллелограммов:
Прямоугольный параллелепипед и его объем. Пирамида. | теория по математике 🎲 стереометрия
У каждого есть представление о параллелограмме из детства, когда он играл в кубики, держал в руке такие предметы, как коробка сока или леденец, или видел аквариум такой формы. В нашей жизни мы постоянно сталкиваемся с объектами, которые представляют собой прямоугольные параллелепипеды (рис. 1).

Рисунок 1
Определение Прямоугольный параллелепипед — это шестиугольник, у которого все грани прямоугольные. Лицо — это плоская поверхность предмета, образующая угол с другой такой же плоской поверхностью. Основания параллелепипеда — это его верхняя и нижняя грани. Например, на рисунке 2 показан прямоугольный кубоид ABCDEFGH с шестью сторонами и основаниями ABCD и EFGH. Кубоид имеет восемь вершин. Они обозначены большими латинскими буквами. Прямоугольный параллелепипед также имеет 12 вершин, которые являются сторонами граней AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
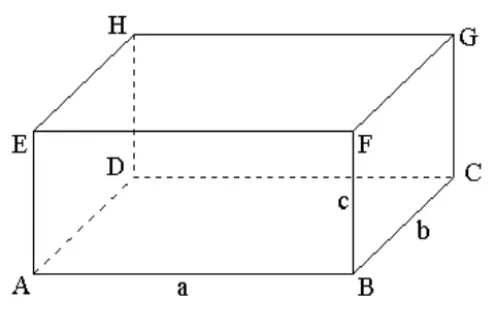
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
Длина, ширина, высота
Прямоугольный параллелепипед имеет три измерения — длину (a), ширину (b) и высоту (c) — рисунок 3. С помощью этих размеров мы можем определить не только площадь каждой стороны, но и площадь всей поверхности параллелепипеда.
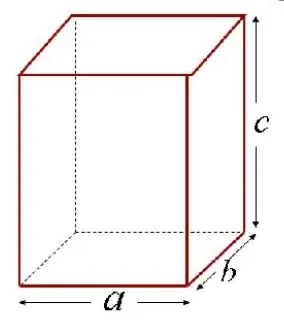
Рисунок 3
Поскольку каждая сторона параллелепипеда является прямоугольником, для нахождения площади каждой стороны нужно перемножить длину и ширину этих сторон, то есть S=ab, S=bc, S=ac. Чтобы найти площадь кубоида, сложите площади всех сторон, то есть площадь S = ab+bc+ac+ab+bc+ac. Поскольку противоположные грани имеют одинаковый размер, их площади также одинаковы, поэтому площадь S = 2ab+2bc+2ac. Это действие можно записать короче, вставив 2 в качестве общего множителя после скобок, т.е. площадь S = 2(ab+bc+ac). Таким образом, площадь можно определить быстрее.
Куб
Прямоугольный параллелепипед, в котором все размеры равны, называется кубом. Поверхность куба состоит из шести одинаковых квадратов (рис. 4).
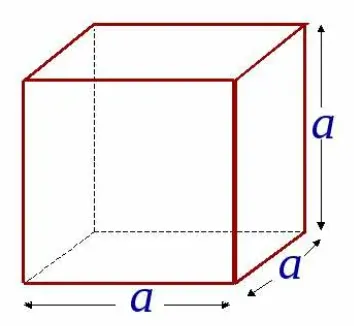
Рисунок 4
Чтобы определить площадь ребра, нужно просто определить площадь квадрата по формуле S=a 2. Чтобы определить площадь поверхности куба, нужно умножить эту площадь на 6, так как у куба шесть равных сторон: S=6a 2
Что такое параллелепипед: определение, элементы, виды, свойства
Данная статья посвящена определению, элементам, формулам и основным свойствам параллелепипеда, включая прямоугольник. Представленная информация дополнена иллюстративными рисунками для лучшего понимания.
Параллелограмм — это геометрическая фигура в пространстве; шестиугольник, грани которого являются параллелограммами. Он имеет 12 граней и 6 торцов.
Параллелограмм — это тип призмы, основанный на параллелограмме. Основные элементы F
Основанием прямолинейного параллелепипеда является параллелограмм. В прямоугольном параллелепипеде боковые грани прямоугольные.
Виды параллелепипедов
- Прямой параллелепипед – боковые грани фигуры перпендикулярны ее основаниям и являются прямоугольниками.
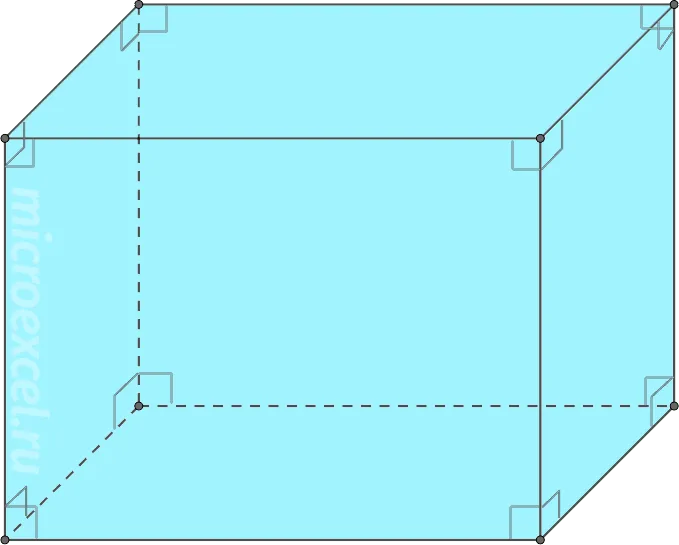
- Прямой параллелепипед может быть прямоугольным – основаниями являются прямоугольники.
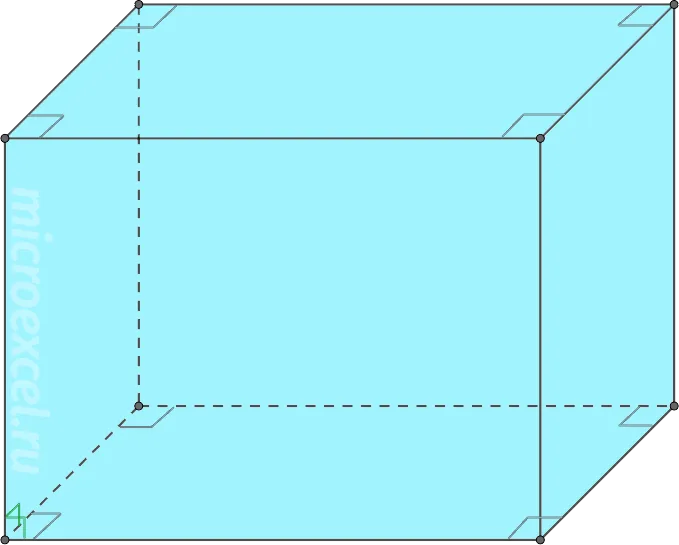
- Наклонный параллелепипед – боковые грани не перпендикулярны основаниям.
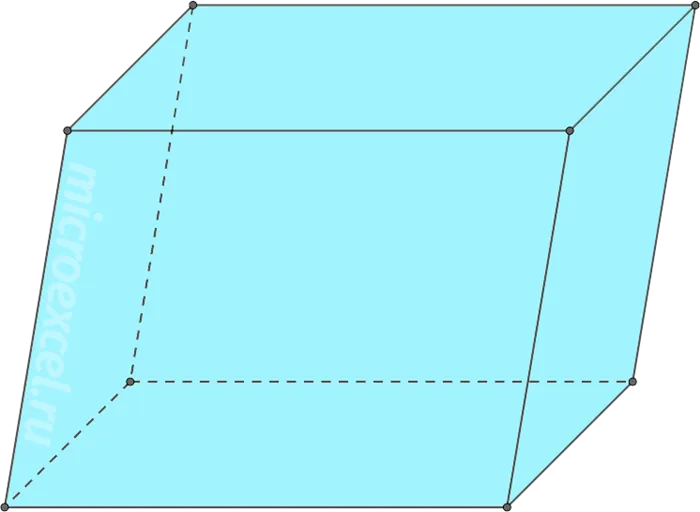
- Куб – все грани фигуры являются равными квадратами.
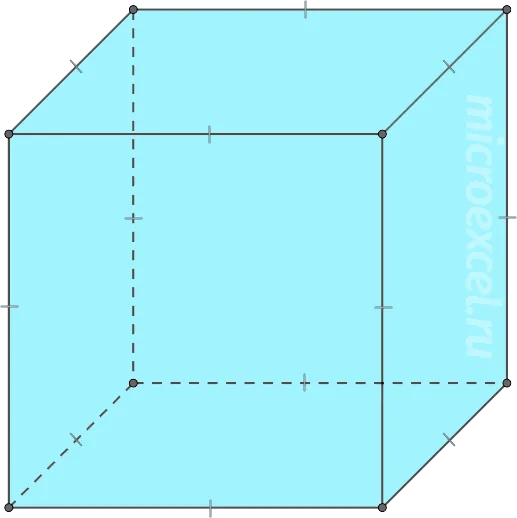
- Если все грани параллелепипеда – это одинаковые ромбы, он называется ромбоэдром .
На иллюстрации: Ребро AA1 перпендикулярно основанию ABCD. A1 перпендикулярна AB и AD, которые лежат в плоскости основания.
Свойства прямолинейного параллелепипеда:
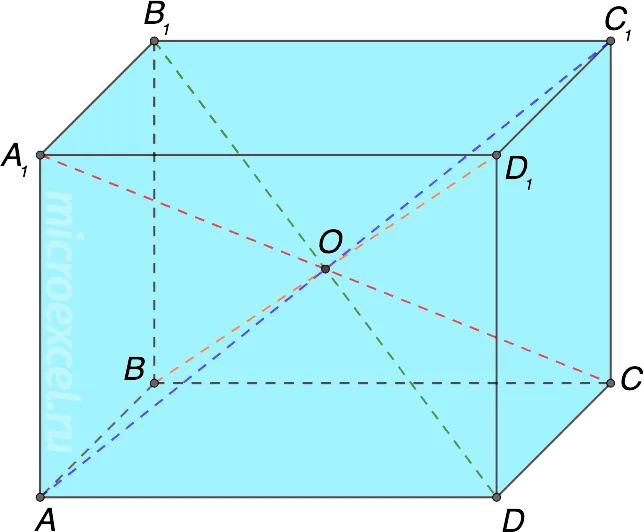
Это звучит довольно заумно и сложно, но на самом деле все свойства просто описывают форму. Прочитайте вслух каждое свойство, глядя на чертеж параллелепипеда после каждой точки. Все сразу встанет на свои места.
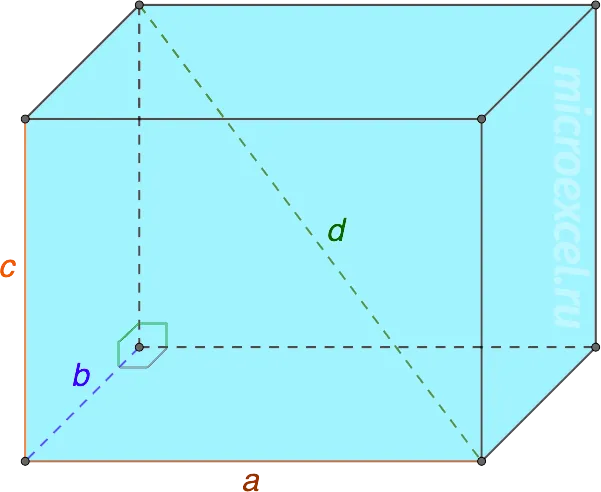
Типы прямолинейных кубоидов:
Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.
Публикации по теме:
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение радиуса шара: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема Фалеса: формулировка и пример решения задачи
- Свойства прямоугольного треугольника
- Свойства равнобедренного треугольника: теория и задача
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства медианы равностороннего треугольника
- Определение и свойства биссектрисы угла треугольника
- Свойства биссектрисы равнобедренного треугольника
- Определение и свойства высоты треугольника
- Формулы для нахождения высоты треугольника
- Свойства высоты равнобедренного треугольника
- Свойства высоты прямоугольного треугольника
- Нахождение радиуса описанной вокруг квадрата окружности
- Что такое ромб: определение, свойства, признаки
- Нахождение радиуса вписанной в ромб окружности
- Что такое окружность: определение, свойства, формулы
- Нахождение площади сегмента круга
- Что такое параллелограмм: определение, свойства, признаки
- Что такое трапеция: определение, виды, свойства
- Свойства равнобедренной (равнобокой) трапеции
- Что такое средняя линия треугольника
- Что такое куб: определение, свойства, формулы
- Что такое шар (сфера): определение, свойства, формулы
- Нахождение площади шарового сегмента
- Нахождение объема шарового слоя
- Что такое конус: определение, элементы, виды
- Основные свойства конуса
- Что такое усеченный конус: определение, основные элементы
- Основные свойства пирамиды
- Что такое правильная пирамида: определение, виды, свойства
- Пирамида с перпендикулярным плоскости основания боковым ребром
- Что такое тетраэдр: определение, виды, формулы площади и объема
Прямой параллелепипед
Дайте определение прямоугольного параллелепипеда:
Параллелепипед — это параллелепипед, основанием которого является прямоугольник, а боковые грани перпендикулярны основанию.
На рисунке: Прямоугольный параллелепипед ABCD; боковое ребро AA1 перпендикулярно ABCD; угол BAD = 90°.
Внимательно посмотрите, как выглядит параллелепипед. Обратите внимание на отличие от прямого параллелограмма.
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
Прямоугольная параллельная плоскость обладает всеми свойствами любой параллельной плоскости.
Формулы для прямоугольного параллелограмма:
- Площадь боковой поверхности прямого параллелепипеда Sб = Ро*h Ро — периметр основания h — высота
- Площадь полной поверхности прямого параллелепипеда Sп = Sб+2Sо Sо — площадь основания
- Объем прямого параллелепипеда V = Sо*h

Прямоугольный параллелепипед
Свойства прямоугольного параллелепипеда
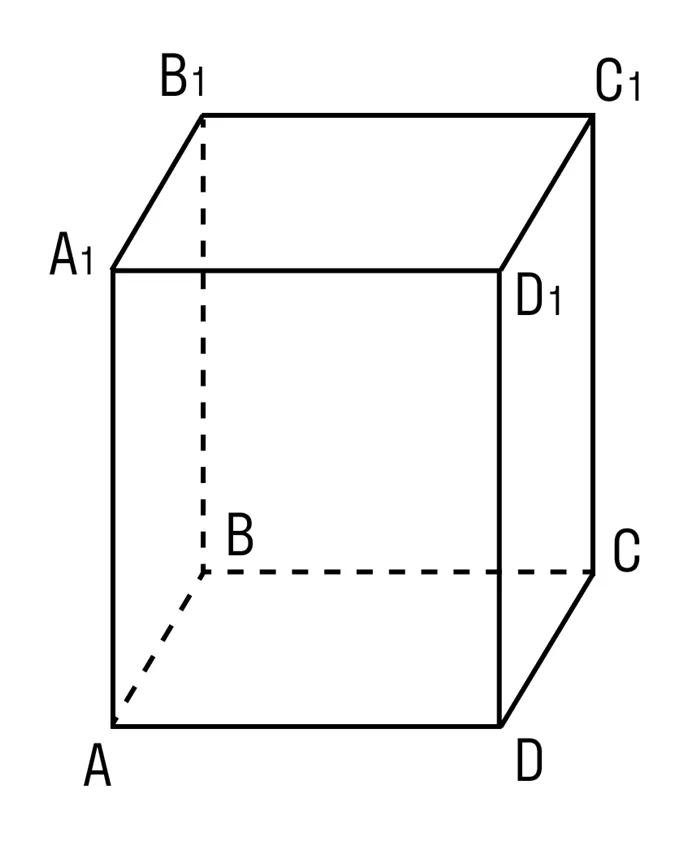
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
- Объем прямоугольного параллелепипеда V = a · b · h a — длина, b — ширина, h — высота
- Площадь боковой поверхности Sбок = Pосн·c=2(a+b)·c Pосн — периметр основания, с — боковое ребро
- Площадь поверхности Sп.п = 2(ab+bc+ac)








