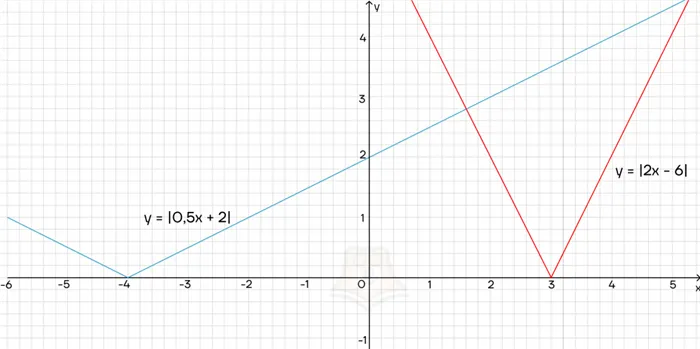
Для иллюстрации приведем графики этих силовых функций: y = x 2 (черный график), y = x 4 (синий график), y = x 8 (красный график). Если α = 2, мы получаем квадратичную функцию, графиком которой является квадратичная парабола.
Определение функции
Определение функции, ее области и диапазона значений. Определения, связанные с обозначением функции. Определения комплексных, арифметических, вещественных, монотонных и полиномиальных функций. Определения максимума, минимума, верхней и нижней границы для ограниченных функций. Ограниченность и продолжение функций.
Функция y = f ( x ) — это закон (правило, отображение), согласно которому каждому элементу x множества X соответствует единственный элемент y множества Y. Множество X называется областью определения функции. Область определения иногда также называют множеством определения или множеством определения функции. Множество значений функции Множество элементов y ∈ Y, имеющих прообразы в множестве X, называется множеством значений функции или областью значений функции. Элемент x ∈ X называется аргументом функции или независимой переменной. Элемент y ∈ Y называется значением функции или зависимой переменной. Атрибут функции Представление самой функции f называется атрибутом функции.
Атрибут f обладает тем свойством, что если два элемента и из множества определений имеют одинаковое значение :, то .
Символ, обозначающий характеристику, может быть тем же, что и символ элемента значения функции. Другими словами, вы можете написать это следующим образом: Напомним, что y — это элемент множества значений функции, и что это правило для сопоставления элемента x с y.
Сам процесс вычисления функции состоит из трех этапов. На первом этапе из множества X выбирается элемент x, затем элемент x отображается на элемент множества Y с помощью правила, и на третьем этапе этот элемент отображается на y.
Частичное значение функции — это значение функции для выбранного (частичного) значения ее определения. График функции f — это множество пар.
Сложные функции
Область определения функции f включает в себя область значений функции g. Тогда каждому элементу t в области определения функции g соответствует элемент x, а этому x соответствует y. Это соответствие называется сложной функцией: Сложную функцию также называют синтезом или суперпозицией функций, а иногда : .
В математическом анализе предполагается, что атрибут функции, обозначаемый одной и той же буквой или символом, определяет одно и то же соответствие. В других дисциплинах, однако, можно встретить другой вид обозначений, при котором представления с одним атрибутом, но разными
Действительные функции
Область функции и множество ее значений могут быть любыми множествами. Например, арифметические последовательности — это функции, область которых — множество натуральных чисел, а множество значений — вещественные или комплексные числа. Векторное произведение также является функцией, поскольку для двух векторов и существует только одно векторное значение. Здесь область определения — это множество всех возможных пар векторов. Множество всех векторов — это множество значений. Логическое выражение — это функция. Его область применения — множество вещественных чисел (или любое множество, в котором определена операция сравнения с элементом «0»). Набор значений состоит из двух элементов — «true» и «false».
Числовые функции играют важную роль в математическом анализе.
Арифметическая функция — это функция, значениями которой являются действительные или комплексные числа. Вещественная или действительная функция — это функция, значениями которой являются вещественные числа.
Максимум и минимум
У вещественных чисел есть операция сравнения. Поэтому множество значений вещественной функции может быть ограничено и иметь наибольшее и наименьшее значение.
Ограниченная сверху (снизу) Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что неравенство выполняется для всех них. Ограниченность Арифметическая функция ограничена, если существует такое число M, что для всех : Максимум M (минимум m ) функции f на множестве X — это такое значение функции при таком значении ее аргумента, при котором для всех, .
Верхняя и нижняя грани
Верхняя граница (точная верхняя граница) функции Верхняя граница или точная верхняя граница вещественной, ограниченной сверху функции — это наименьшее число, которое ограничивает сверху область значений функции. Это такое число s, для которого: 1) для всех ? 2) для каждого, существует такой срок, на который значение функции превышает s′: Верхняя граница функции может быть задана следующим образом: Верхняя граница функции, которая не ограничена сверху, — это бесконечно удаленная точка из. Нижняя граница (точная нижняя граница) функции Нижняя граница или точная нижняя граница вещественной функции, которая ограничена снизу, — это наибольшее число, которое ограничивает диапазон ее значений снизу. Это такое число i, для которого: 1) для всех ? 2) для каждого, существует такой аргумент, значение функции которого меньше i′: Нижняя граница функции может быть задана следующим образом: Нижняя граница функции, ограниченной снизу, — это бесконечно удаленная точка из .
Таким образом, каждая вещественная функция на непустом множестве X имеет верхнюю и нижнюю границы. Но не каждая функция имеет максимум и минимум.
В качестве примера рассмотрим функцию на открытом интервале
Нет ничего необычного в том, что в жизни существует взаимосвязь между различными ценностями. Предположим, что вход в зоопарк содержит информацию о стоимости билетов. Для детей до 7 лет вход бесплатный, для детей от 8 до 18 лет билет стоит 100 рублей, а для взрослых — 200 рублей. Поэтому цена билета зависит от возраста покупателя. Математики говорят в этом случае, что цена билета является функцией возраста посетителя.
Что такое функция
Возьмем выражение 2s + 5. Обозначим его значение переменной d. Для каждого значения s мы можем вычислить соответствующее ему значение d. Если s = 5, то
и для s = 10 мы имеем
Оказывается, что значение d однозначно определяется s, т.е. d является функцией от s .
Попробуем дать строгое определение функции. Как и во многих других определениях в математике, в нем используется понятие множества.
Обозначим через D множество всех тех чисел, которые можно подставить вместо d в функцию. Очевидно, что это множество всех действительных чисел. Аналогично, обозначим через S множество всех значений, которые может принимать s.
определяет правило, согласно которому каждому элементу D присваивается элемент множества S. В этом контексте мы можем сформулировать определение:
Множество S называется областью определения функции, а множество D — областью значений функции. Величина s называется независимой переменной, независимой переменной или просто аргументом, потому что мы можем придать ей любое значение. Термин зависимая переменная, зависимая переменная или просто функция используется для величины d, поскольку ее значение зависит от значения, выбранного для аргумента. Другими словами, аргумент и функция — это две величины, одна из которых (независимая) определяет другую (зависимую). Иногда встречается условное обозначение:
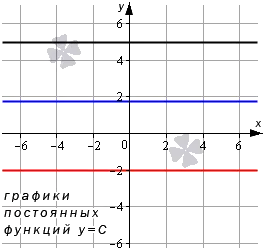
Буква s в скобках означает, что d зависит именно от переменной s. Другой пример: u( t) — это функция, где t — независимая переменная, а u — переменная, зависящая от аргумента.
Иногда необходимо определить значение функции для определенного значения аргумента. В этом случае аргумент заключается в круглые скобки:
d(-100) = 2*(-100) + 5 = -195
Поэтому, если нам нужно определить значение функции y(x), когда x равно 7, например, мы напишем y(7).
Давайте сделаем несколько уточнений. Во-первых, величины, между которыми устанавливается соответствие, не обязательно должны быть числовыми. Например, если стоимость корпуса мобильного телефона зависит от его цвета (синий, желтый, красный), то эту стоимость можно считать функцией цвета, которая не описывается числом. Если для каждого кассира, работающего в магазине, можно определить, где находится кассовый аппарат, то можно определить количество кассовых аппаратов.
Наиболее распространенным методом определения функции в алгебре является аналитический. Для этого необходимо написать формулу, которая позволит вам использовать значение независимой переменной для расчета зависимой переменной:
Способы задания функции
Эти записи аналогичны другим, где аргумент явно указан в круглых скобках после зависимой переменной:
Иногда функцию можно представить в виде алгоритма. Например: «Чтобы вычислить значение g(x), сложите все десятичные знаки натурального числа x». Для аргумента 135 функция будет считать 9:
g(135) = 1 + 3 + 5 = 9
Вот еще несколько значений этой функции:
g(5656) = 5 + 6 + 5 +6 = 22
Подобный подход не редкость в некоторых языках программирования.
Если область функции не содержит бесконечного числа чисел, ее можно задать в виде таблицы, указав все возможные значения независимых переменных и соответствующие значения зависимых переменных. Ниже приведен пример матричной функции, определяющей соответствие между европейскими и английскими размерами мужских пальто:
А вот еще одна табличная функция, которая присваивает каждому натуральному числу n от 1 до 5 число, равное 2n + 3:
Из приведенной выше таблицы легко увидеть, что
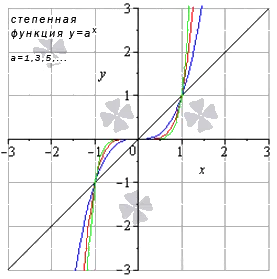
Графический способ определения функций очень распространен. Он требует, чтобы была построена диаграмма (линия или серия линий в координатной плоскости), которая может быть использована для определения зависимой переменной на основе ее определения. Эта диаграмма может иметь следующий вид:
Координатная плоскость показывает горизонтальную ось, на которой откладывается значение независимой переменной (в данном примере это x), и вертикальную ось, на которой откладывается зависимая переменная (y). Сам график представлен синей линией. Покажем, как мы можем использовать его для нахождения значения y. Предположим, нам нужно найти y(2), то есть значение y при x = 2. Найдите число 2 на горизонтальной оси x (также называемой осью абсцисс) и проведите от нее перпендикулярную линию до пересечения с диаграммой:
Затем проведите горизонтальную линию от этой точки до пересечения с вертикальной осью y (также называемой осью ординат):
Затем внимательно посмотрите, где горизонтальная линия пересекает ось y. В этом случае y(2) = — 2,5.
Мы можем сформулировать определение графика функции:
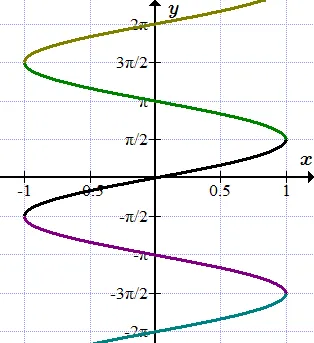
Мы должны понимать, что не каждая строка определяет функцию. Дело в том, что никакая вертикальная линия не может пересекать график в 2 или более точках, потому что тогда одному значению аргумента соответствует много значений функции; такая ситуация показана на рисунке:
Иногда одну и ту же взаимосвязь можно описать как аналитически, так и графически
С помощью современных компьютерных технологий можно практически мгновенно рассчитать положение миллионов таких точек. Если соединить их все плавной линией, получится график:
Построение графика функции
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось OX в своих корневых точках ( x
; 0) и ( x
; 0). Если корней нет, то квадратичная функция не пересекает ось OX; если корень есть, то это означает, что функция не пересекает ось OX в данной точке ( x ; 0).
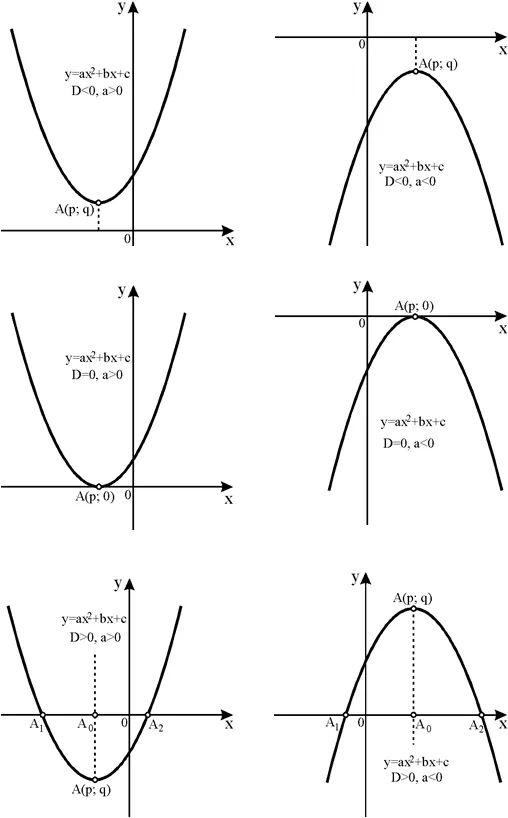
; 0), квадратичная функция только касается оси OX, но не пересекает ее. Квадратичная функция всегда пересекает ось OY в точке (0 ; c ). График квадратичной функции (параболы) может иметь следующий вид (на рисунке приведены примеры, которые далеко не охватывают все возможные виды парабол):
Координаты вершины параболы можно вычислить по следующим формулам. X вершины ( p — на рисунках выше) параболы (или точки, в которой квадратичная тройка достигает своего наибольшего или наименьшего значения):
X вершины ( q на рисунках выше) параболы, или максимум, когда ножки параболы направлены вниз ( a
0), значение квадратного треугольника:
График квадратичной функции (Парабола)
Функция мощности — это функция, заданная формулой:
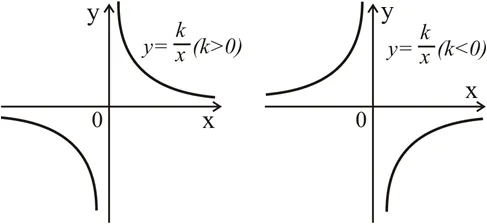
Вот несколько примеров графиков силовых функций:1Обратно пропорциональная зависимость — это функция, заданная формулой:2В зависимости от знака числа k график обратной функции может иметь два основных варианта:0Асимптотика — это линия, на которой линия графика функции приближается к бесконечности, но не пересекает ее. Асимптоты для графиков обратных соотношений, показанных на рисунке выше, — это координатные оси, на которых график функции приближается к бесконечности, но не пересекается.
Экспоненциальная функция относительно α — это функция, заданная следующей формулой:
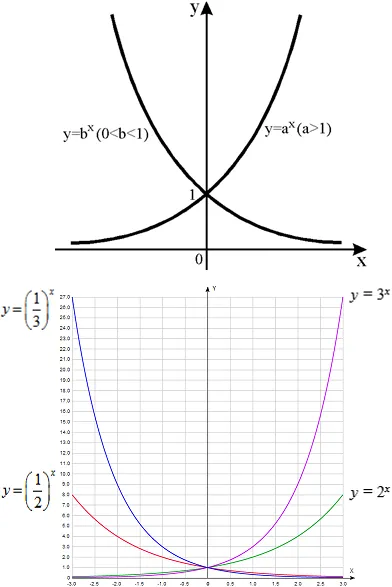
В зависимости от того, больше или меньше единицы число α, график экспоненциальной функции может иметь два основных варианта (мы также приводим примеры, см. ниже):<0), либо минимальное, если ветви параболы направлены вверх ( a>Логарифмическая функция — это функция, заданная формулой:
Графики других функций
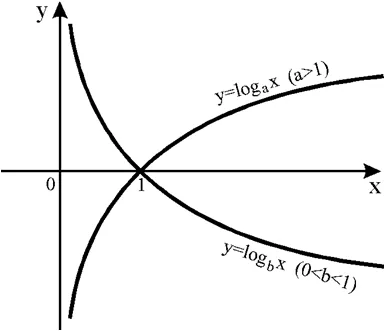
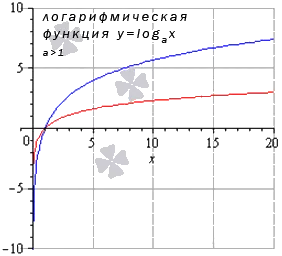
В зависимости от того, больше или меньше единицы число a, график логарифмической функции может иметь два основных варианта:
График функции y = | x | имеет следующий вид:
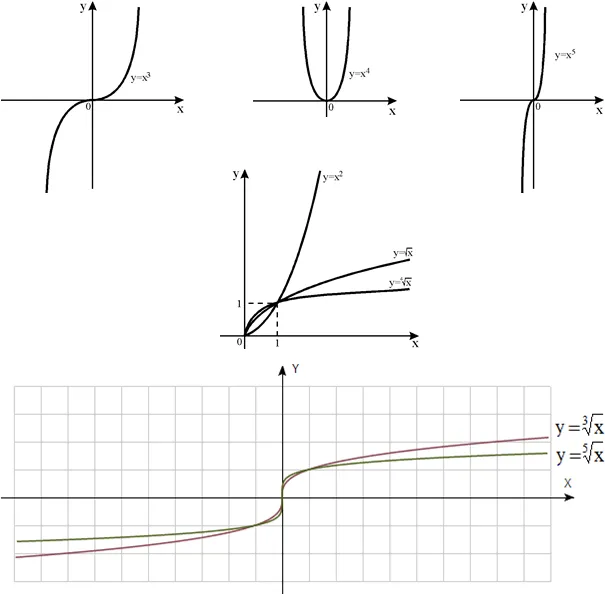
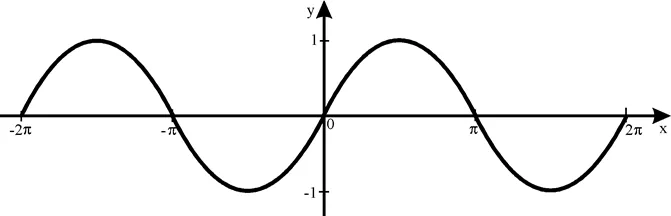
Функция y = f ( x ) называется периодической, если существует ненулевое число T такое, что f ( x + T ) = f ( x ) для каждого x в области определения функции f ( x ). Если функция f ( x ) периодическая с периодом T.
Вот: A, k, b постоянные числа, где k не равно нулю, также периодические с периодом T
который определяется как
Если дана функция, принимающая значения в множестве set, то
Наличие функциональной связи между элементом.
Определение функции можно легко обобщить на функцию с несколькими пределами.
Если множество, то представление является локальным представлением, а элементы упорядоченного множества называются аргументами (т.к.
. Однако этот метод совершенно не подходит для функций на бесконечных множествах (которыми являются обычные вещественные функции: динамические, линейные, экспоненциальные, логарифмические и т.д.).
Графики периодических (тригонометрических) функций
Следующее выражение используется для определения функции: Есть переменная, которая охватывает область определения функции, а x и y могут охватывать любое множество объектов любого вида. Это могут быть числа, векторы, матрицы, яблоки или цвета радуги. Поясним это на примере:
Допустим, есть набор из яблока, самолета, груши, стула и набор из человека, локомотива, квадрата. Пусть функция f имеет следующий вид: (яблоко, человек), (самолет, локомотив), (груша, квадрат), (стул, человек). Если ввести переменную x, которая охватывает множество, то функцию можно определить аналитически как:1Числовые функции могут быть определены аналогичным образом. Пример: Если x охватывает множество вещественных чисел, то это задает функцию f. Важно понимать, что само выражение не является функцией. Функция как объект представляет собой множество (упорядоченных пар). Это выражение как объект представляет собой равенство двух переменных. Она определяет функцию, но не является функцией.
Во многих областях математики, однако, можно использовать f(x) для обозначения как самой функции, так и аналитического выражения, которое ее определяет. Эта синтаксическая конвенция чрезвычайно практична и оправдана.
Числовые функции также могут быть определены с помощью графика. Скажите
Рассмотрим (n+1)-мерное линейное пространство над диапазоном вещественных чисел (так как функция вещественная) и выберем произвольный базис в этом пространстве (. Таким образом, получим набор векторов линейного пространства, соответствующих точкам заданной функции по заданному правилу. Точки соответствующего ассоциированного пространства образуют поверхность.
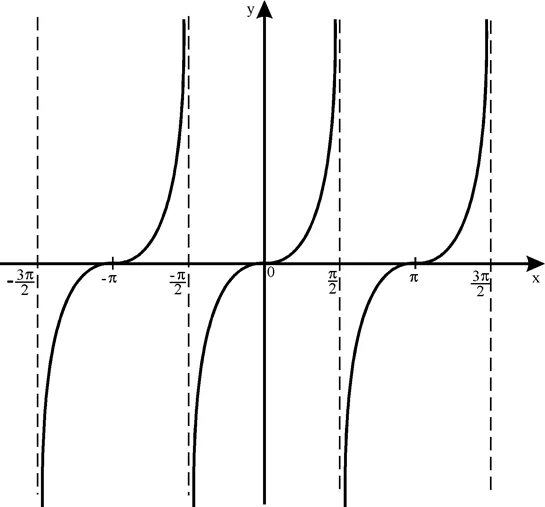
Если рассматривать евклидово пространство свободных геометрических векторов (направленных отрезков прямых) как линейное пространство и число границ функции f не превышает 2, то можно визуально представить это множество точек в виде рисунка (графика). Если считать начальную точку ортонормой, то мы получим «школьное определение» графика функции.
Обозначения
Для функций с 3 и более аргументами такое представление неприменимо из-за отсутствия геометрической интуиции для многомерных пространств.
- этот факт коротко записывают в виде<\longrightarrow>Y» width=»» height=»» />.
- область определения функции ) обозначается \,f» width=»» height=»» />;
- область значений функции ) обозначается ), или ( ).
Но даже для таких функций мы можем получить наглядное полугеометрическое представление функции.
- наиболее часто обозначается как или
- реже используется обозначение без скобок или
- а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: ;
- так же существует и операторное обозначение
Функции нескольких аргументов
Отображения, которые имеют одинаковое поле определения и поле значения, называются отображениями или преобразованиями множества к самому себе.
В частности, преобразование множества
» width=»» height=»» />.
В этом случае » width=»» height=»» />.
Способы задания функции
Аналитический способ
Функция, как математический объект, представляет собой бинарное отношение, удовлетворяющее определенным условиям. Функцию можно задать непосредственно как множество упорядоченных пар, например: есть функция \;» width=»» height=»» />называется идентичным.
Для такого отображения существует специальная нотация: (если из контекста понятно, какое множество имеется в виду). Это обозначение происходит от английского слова identity.
Другое обозначение для преобразования тождества: Преобразование тождества поэтому часто называют унитарным.
Пусть есть два задания, для которых область значений первого задания является подмножеством области определения второго задания. Тогда для каждого такого, что однозначно идентифицирует элемент из. То есть, для каждого из следующих элементов.
Такое представление называется синтезом карт и обозначается через
Графический способ
более
Такое отображение называется обратным от
Отображение, для которого определена обратная величина, называется инвертируемым.
Что касается композиции функции, то свойство обратимости — это одновременное выполнение двух условий: и .
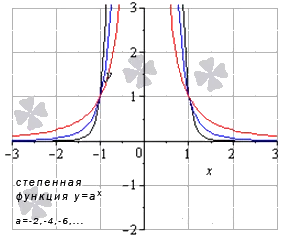
На следующем рисунке показаны примеры графиков степенной функции y = x a, когда a — четное отрицательное число: y = x — 8 (черный график); y = x — 4 (синий график); y = x — 2 (красный график).
Связанные определения
Сужение и продолжение функции
1 .
Построим график степенной функции y = x a при заданных условиях на примере следующих функций: y = x 5 4, y = x 4 3, y = x 7 3, y = x 3 π (черный, красный, синий и зеленый графики соответственно).
1 дает аналогичный вид графика.
На следующем графике изображены графики силовых функций y = x — 5 4, y = x — 5 3, y = x — 6, y = x — 6, y = x — 24 7 (цвета кривых черный, красный, синий и зеленый соответственно).
Образ и прообраз (при отображении)
1 ) .
Проиллюстрируем этот частный случай представлением экспоненциальных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет кривой).
,
Другие базовые значения больше единицы дают похожий вид графика экспоненциальной функции.
1. На следующем рисунке изображены графики логарифмических функций y = log 3 2 x и y = ln x (синяя и красная кривая соответственно).
» width=»» height=»» />,
При других значениях основания, больших единицы, график выглядит аналогично.
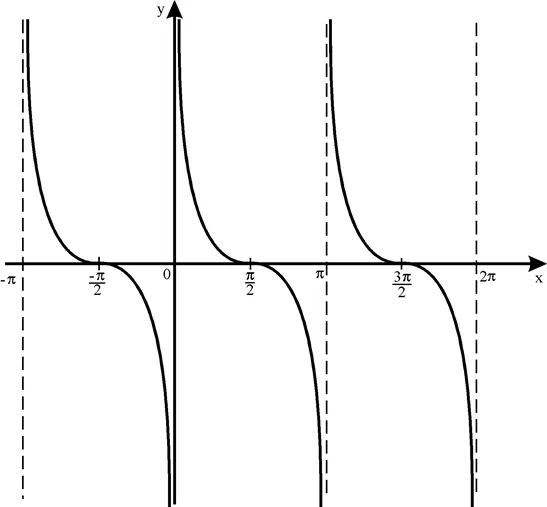
В том частном случае, когда множество » width=»» height=»» />, множество )=\» width=»» height=»» />График данной функции называется косинусом.
Тождественное отображение
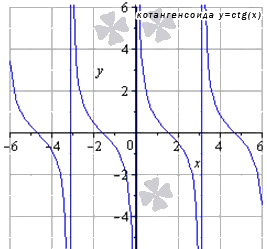
График данной функции называется котангенсом.
Свойства аркагональной функции:
,
Композиция отображений
.
- либо ,
- либо
Обратное отображение
Если отображение \colon Y\to X» width=»» height=»» />
- область определения (множество ;
- область значений (множество тогда и только тогда, когда
Степенная функция при четном отрицательном показателе степени
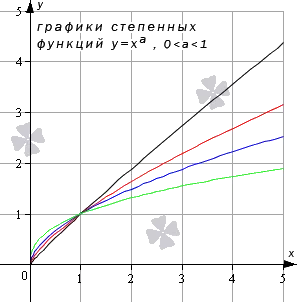
Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)
Разберем степенную функцию y = x a, когда показатель степени – нецелое рациональное или иррациональное число при условии, что a>
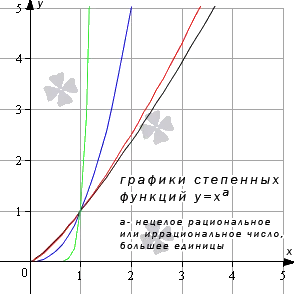
Иные значения показателя степени а при условии a>
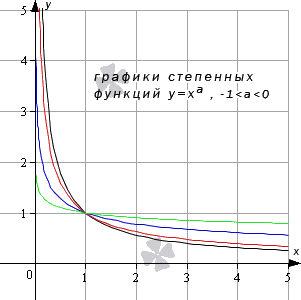
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)
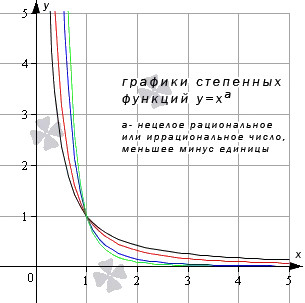
Теперь рассмотрим случай, когда основание показательной функции больше, чем единица ( а>
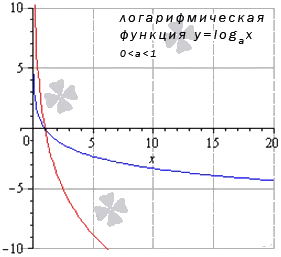
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а>
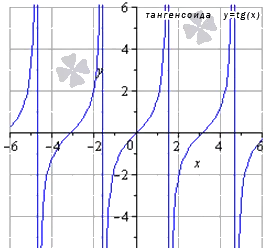
- Функция косинус: y = cos ( х )
- Функция котангенс: y = c t g ( х )
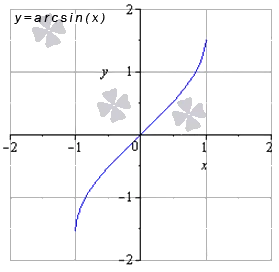
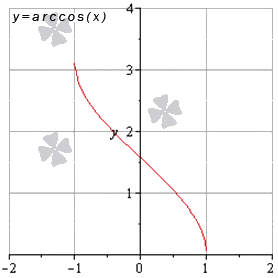
- Функция арккосинус: y = a r c cos ( х )
- Функция арккотангенс: y = a r c c t g ( х )
- область определения: x ∈ — ∞ ; + ∞ ;
- область значений: y ∈ ( 0 ; π ) ;
- данная функция – общего вида;
- функция является убывающей на всей области определения;
- функция арккотангенс имеет вогнутость при x ∈ 0 ; + ∞ ) и выпуклость при x ∈ ( — ∞ ; 0 ;
- точка перегиба имеет координаты 0 ; π 2 ;
- горизонтальные асимптоты – прямые y = π при x → — ∞ (на чертеже – линия зеленого цвета) и y = 0 при x → + ∞ .