Вычисление неизвестных сторон и углов треугольника из известных сторон и углов всегда называлось «решением треугольников». Используются общие тригонометрические теоремы, упомянутые выше.
Треугольник
Треугольник (в евклидовом пространстве) — это геометрическая фигура, состоящая из трех отрезков, соединяющих три точки, которые не лежат на одной прямой. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют три угла при вершинах треугольника. Другими словами, треугольник — это многоугольник, имеющий ровно три угла. Если три точки лежат на прямой, то «треугольник» с вершинами в трех определенных точках называется вырожденным. Все остальные треугольники не являются вырожденными.
В неевклидовых пространствах геодезические линии действуют как стороны треугольника, которые обычно криволинейны. Поэтому такие треугольники называются криволинейными.
Содержание
- 1 Элементы треугольника
- 2 Признаки равенства треугольников
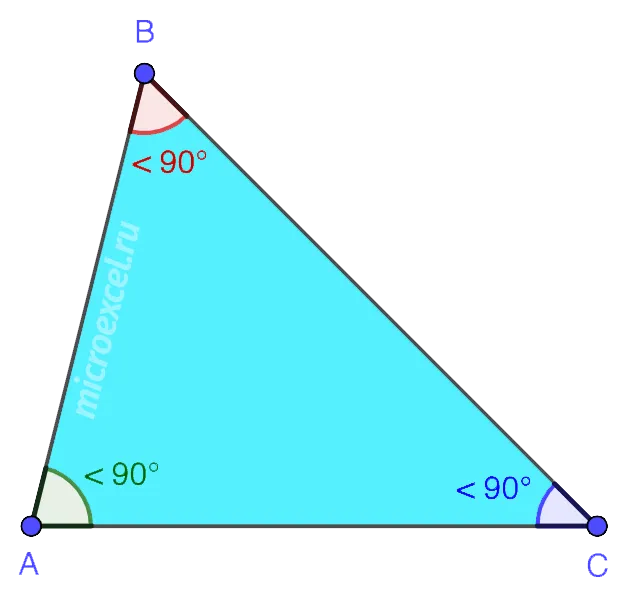
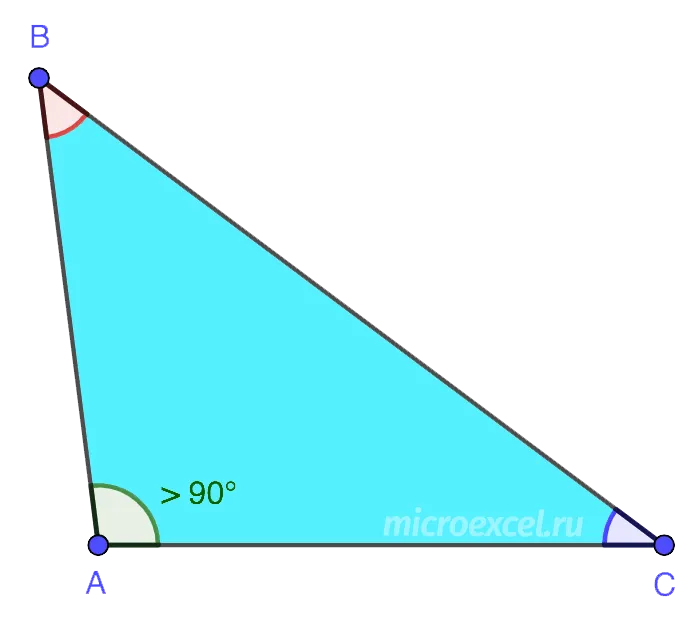
- 3 Типы треугольников
- 3.1 По величине углов
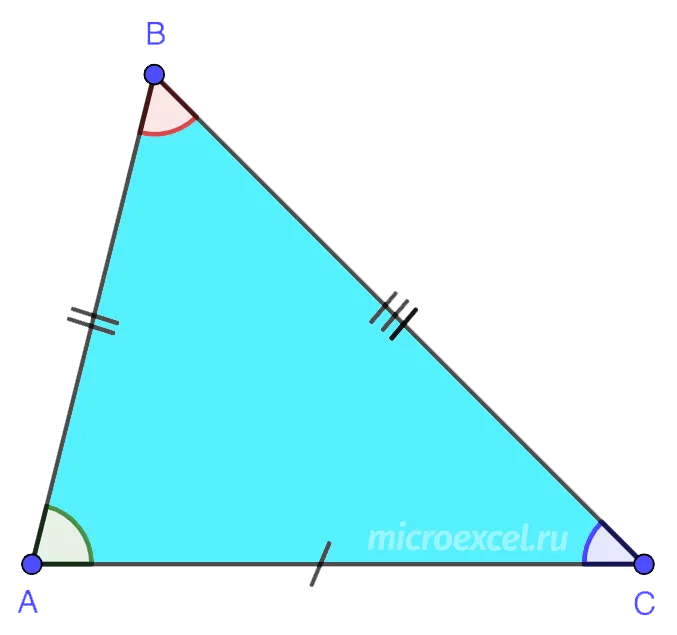
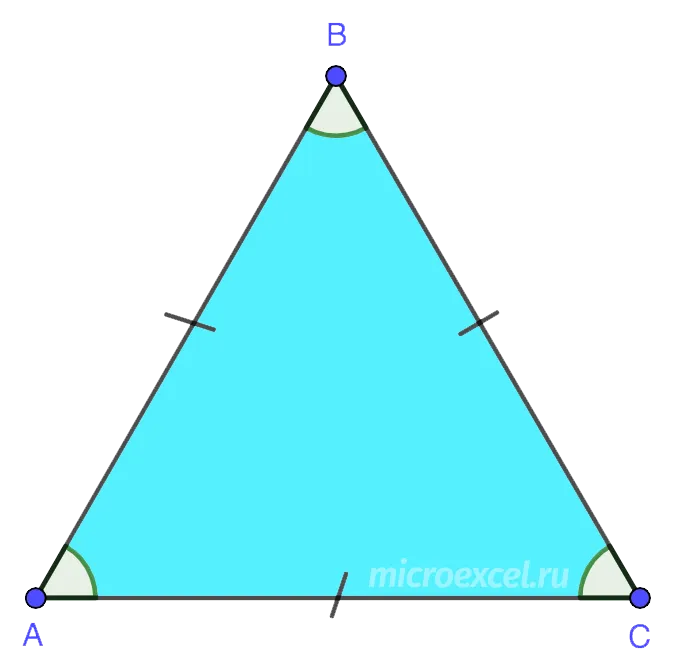
- 3.2 По числу равных сторон
- 4.1 Лучи, отрезки и точки
- 4.2 Прямые
- 4.3 Треугольники
- 4.4 Окружности
- 4.5 Эллипсы, параболы и гиперболы
- 4.6 Преобразования
- 4.7 Кубики
- 5.1 Неравенство треугольника
- 5.2 Теорема о сумме углов треугольника
- 5.3 Теорема синусов
- 5.4 Теорема косинусов
- 5.5 Теорема тангенсов
- 5.6 Прочие соотношения
- 5.7 Решение треугольников
- 6.1 Вычисление площади треугольника в пространстве с помощью векторов
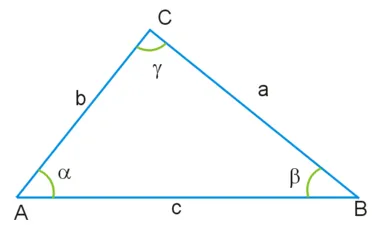
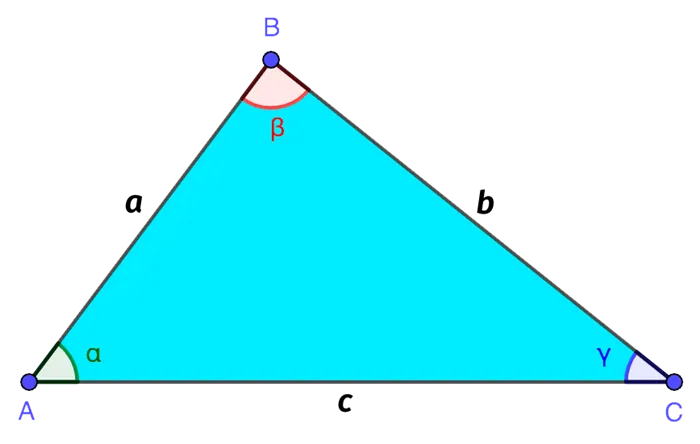
Треугольник с вершинами A, B и C обозначается следующим образом (см. рисунок). У треугольника три стороны:
-
Сторона
Сторона
СторонаДлины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):
Треугольник
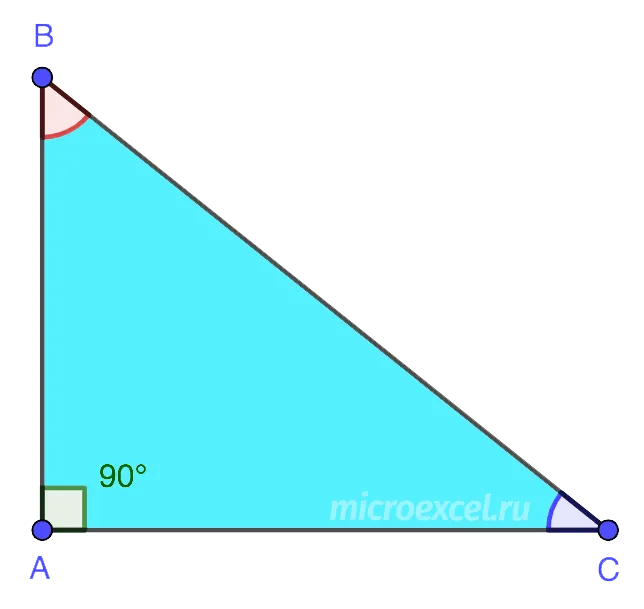
- угол и ;
- угол угол — угол, образованный сторонами
Углы при соответствующих вершинах традиционно обозначаются греческими буквами (a, b, c).
Признаки равенства треугольников
Треугольник в евклидовой плоскости может быть однозначно определен (конгруэнцией) следующими базовыми элементами-треугольниками:
- a, b, γ (равенство по двум сторонам и углу лежащему между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Точки равенства правильных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
В сферической геометрии и геометрии Лобачевского существует точка равенства треугольников с тремя углами.
Треугольник
Треугольник — это замкнутая полилиния, состоящая из трех элементов:
Вершины полилинии называются вершинами треугольника, а ее члены — сторонами треугольника. Углы, образованные двумя сторонами треугольника, называются углами треугольника:
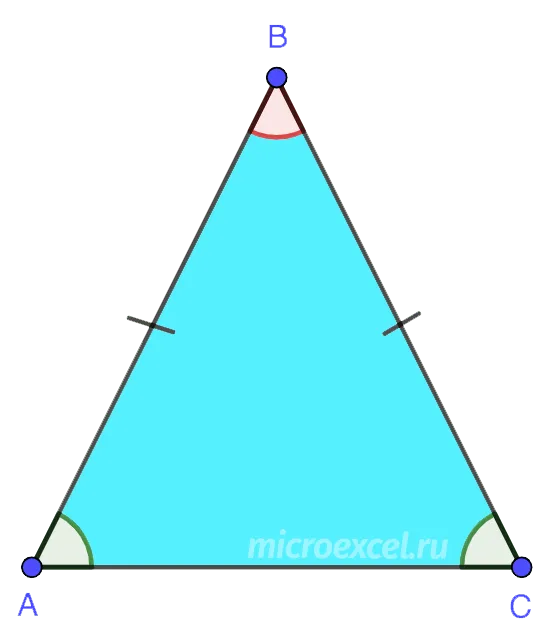
В треугольнике ABC вершины A, B и C являются вершинами треугольника, а связи AB, BC и CA — сторонами треугольника. Три угла ∠ABC, ∠BCA и ∠CAB являются углами треугольника. Часто углы треугольника обозначаются одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, расположенными в его вершинах. Например, треугольник ABC, или BCA, или CBA. Слово «треугольник» часто заменяется словом «треугольник», так что написание «ABC» может звучать так: «треугольник ABC».
Каждый треугольник имеет 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, проведенный из вершины треугольника к его основанию. Высота треугольника также может падать на продолжение основания.
Отрезок BN — высота ABC, EL — высота DEF, которая падает на продолжение DF.
Высота — это длина отрезка от вершины угла до пересечения с
По условию, треугольники равны. Поэтому мы применяем правило, описанное выше, которое гласит, что все соответствующие элементы фигуры равны друг другу.
Виды треугольников
Если ∆ABC = ∆A
то соответствующие стороны равны:
и соответствующие углы равны:
Геометрия интересна тем, что большинство ее правил можно доказать. Такие правила называются теоремами.
Равенство треугольников
В то же время существуют собственные правила, называемые аксиомами геометрии.
Сегодня мы разберем первую теорему «Первое доказательство равенства треугольников» и соберем доказательства для этой теоремы.1B1C1Два треугольника — это ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.
Докажите, что ∆OMN=∆KLT.
Докажите первое доказательство того, что треугольники равны:1B1C1,Поскольку мы знаем, что соответствующие углы равны ∠M =∠L, мы можем наложить два треугольника так, чтобы вершина M совпала с вершиной L.
Тогда сторона OM накладывается на сторону KL, а сторона MN накладывается на отрезок LT. По условию мы знаем, что отрезки OM=KL, MN=LT, поэтому они совпадают. Получается, что при суперпозиции угол и две стороны совпадают, поэтому оставшиеся стороны ON и KT также совпадают, т.е. ON = KT. Если суперпозиция трех сторон и одной вершины совпадают, то две другие вершины KO и TN также совпадают.
Оказывается, что все элементы ∆ согласуются, и такой ∆ называется равным.
Мы доказали, что ∆OMN=∆KLT.
Нам также необходимо ознакомиться с некоторыми понятиями, без которых невозможно продолжать изучение геометрии.
Проведем линию AB. Выберите точку, которая не лежит на этой прямой. Начертите отрезок C, соединяющий C с прямой AB так, чтобы в точке пересечения C с AB был прямой угол (90˚). Отрезок C называется перпендикуляром к линии.
Доказательство теоремы проводится в два этапа.
Шаг 2
Рассмотрим ∆ABC. Отметьте середину отрезка AC и назовите ее точкой O. Соедините B и O отрезком. Полученный отрезок BO называется медианой.
Каждая треугольная фигура имеет три вершины, из каждой из которых можно провести медиану, так что в одной фигуре можно провести три медианы.
Чтобы рассмотреть понятие биссектрисы треугольника, необходимо вспомнить определение биссектрисы угла:
На рисунке показан ∆ОВМ. Из точки O проведите биссектрису (радиус, делящий угол пополам) и продлите ее до точки пересечения со стороной BM. Обратите внимание на точку пересечения C. OC делит угол O пополам (∠BOS =∠COM) и пересекает противоположную сторону Bm.
Рисунок показан на рисунке RTC. Нарисовать
Медиана, биссектриса, высота
Биссектриса
Минутка истории:
- Ученые установили, что первые упоминания о треугольниках появились еще четыре тысячи лет назад и были отображены на египетских папирусах. Две тысячи лет назад изучение данной геометрической фигуры приняло большие масштабы.
- Жители Китая уверенны, что именно треугольник является шаблоном для всех существующих фигур, которые представляют собой видоизмененные треугольники.
- Самый популярный треугольник в мире – Бермудский. Его название появилось в пятидесятых годах из-за расположения материковых вершин (Бермуды, Флорида, Пуэрто-Рико) и аномальных явлений между ними.
Примеры задач
<8<11 + 4 8 – 4<11<8 + 4 11 – 8<4<11 + 8
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Теорема Менелая: формулировка и пример с решением
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Свойства прямоугольного треугольника
- Свойства равнобедренного треугольника: теория и задача
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника








