Добрый вечер! Мы очень рады, что нам посчастливилось найти такого замечательного и удивительного преподавателя, как Анастасия Сергеевна! Она проводит занятия в очень интересной форме, и ребенок с энтузиазмом принимает их. Вы сразу чувствуете, что она талантливый человек. Мы уже с нетерпением ждем следующего урока.
Перпендикулярность в пространстве с примерами решения
В этом разделе вы изучите понятия угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями, узнаете, что такое прямоугольная проекция, и исследуете свойство прямоугольной проекции многоугольника.
Поскольку две пересекающиеся линии в пространстве лежат в одной плоскости, мы определяем угол между ними так же, как и в планетометрии. Определение. Угол между двумя пересекающимися прямыми — это угол, принадлежащий одной из пересекающихся прямых и не больше (рис. 33.1).
Угол между двумя параллельными прямыми называется .
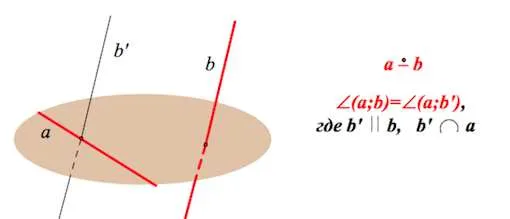
Ввести понятие угла между пересекающимися линиями. Определение. Угол между двумя пересекающимися прямыми — это угол между пересекающимися прямыми, каждая из которых параллельна данной пересекающейся прямой.

Линии M пространства рисуют линии (рисунок 33.2). По определению, угол между пересекающимися линиями равен .
Естественно возникает вопрос: зависит ли угол между некоторыми пересекающимися прямыми от M? Следующая теорема помогает ответить на этот вопрос.
Теорема 33.1 Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, каждая из которых параллельна данным прямым.
Теорему 33.1 можно использовать для доказательства того, что угол между двумя пересекающимися прямыми равен, где
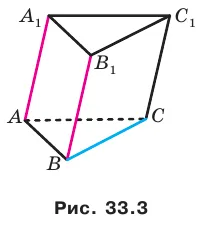
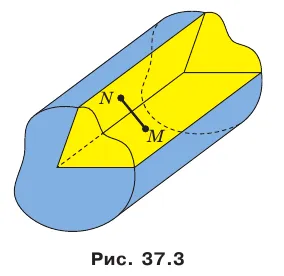
Например, на рисунке 33.3 изображена треугольная призма, а BC равен углу между пересекающимися линиями BC .
Определение. Две линии в пространстве считаются перпендикулярными, если угол между ними равен 90°.
Обратите внимание, что перпендикулярные линии могут либо пересекаться, либо скрещиваться.
Два отрезка в пространстве считаются перпендикулярными, если они лежат на перпендикулярных прямых.
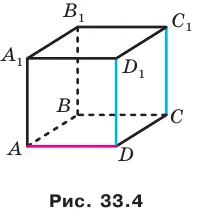
Например, ребра AD и AD перпендикулярны друг другу (рисунок 33.4). Поскольку AD и AD и, следовательно
Пример:
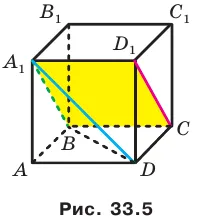
На рисунке 33.5 показаны куб и
Решение:
Соедините точки, тогда точки параллельных прямых равны углам B и D. Сегменты равносторонние. Тогда ответ: 60°.
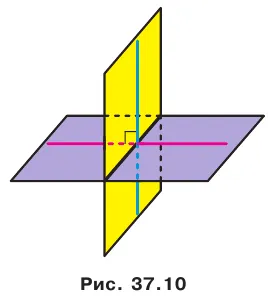
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: Флагшток перпендикулярен земле (рис. 34.1), мачты парусного судна перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивается в доску перпендикулярно поверхности (рис. 34.3) и т.д.

Эти примеры дают представление о прямой линии, перпендикулярной плоскости. Определение. Линия перпендикулярна плоскости, если она перпендикулярна к
Теорема 34.1 часто используется на практике. Например, основание рождественской елки имеет форму креста. Если дерево разместить так, чтобы ствол был перпендикулярен направлениям креста, то дерево также будет перпендикулярно плоскости земли (Рисунок 34.6).
Выскажем теорему, которую можно рассматривать как дальнейшее доказательство перпендикулярности прямой и плоскости.
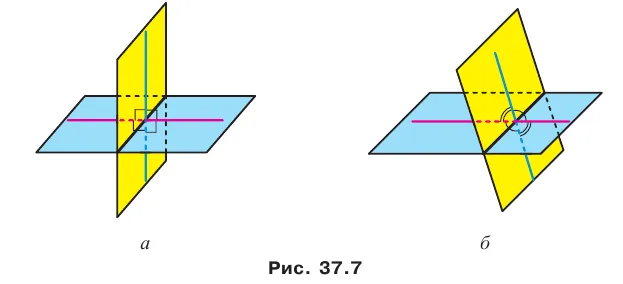
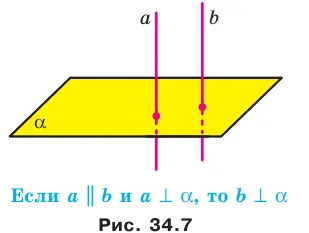
Теорема a 34.2 Если одна из двух параллельных прямых перпендикулярна плоскости, то другая прямая также перпендикулярна этой плоскости (рис. 34.7).

Например, на рисунке 34.5 линии ABC и ABC являются одной линией, поэтому, согласно теореме 34.2, линия ABC. Проиллюстрируем теорему как отражение параллельности двух прямых.
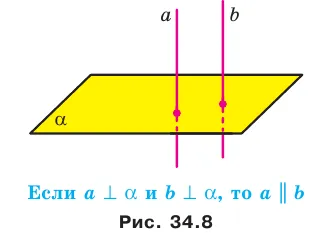
Теорема a 34.3 Если две прямые перпендикулярны одной плоскости, то они параллельны (рис. 34.8). Эта теорема также справедлива.
Теорема 34.4: Через заданную точку можно провести прямую, перпендикулярную заданной плоскости, и только одну.
Пример:

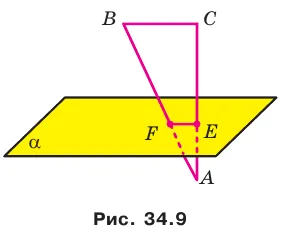
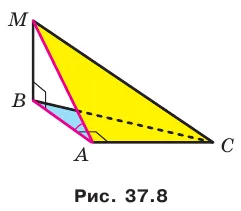
Плоскость AC правильного треугольника ABC пересекает катет AC в точке E и гипотенузу AB в точке F (рисунок 34.9). Найдите отрезок EF, если AE : EC = 3 : 4, BC = 21 см.
Рисунок представляет собой ортогональную проекцию F на плоскость.
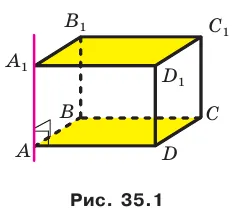
Например, основание ABCD кубоида в плоскости ABC в направлении линии
В дальнейшем, когда мы говорим о проекции фигуры, мы имеем в виду ортогональную проекцию, если не указано иное.
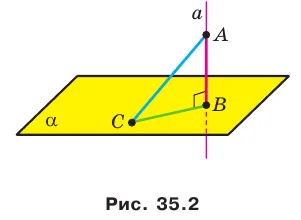
Обозначим плоскость, перпендикулярную плоскости (рисунок 35.2).
Пример:
Отметим плоскость AC (рис. 35.2), а прямая AS называется наклонной, проведенной из A к плоскости как основанию наклонной. Линия BC является проекцией наклона BC .
Перпендикуляр и наклонная
Теорема 35.1 Если из одной и той же точки плоскости проведены перпендикуляр и наклон, то наклон больше перпендикуляра.
Пример:
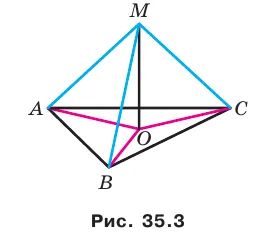
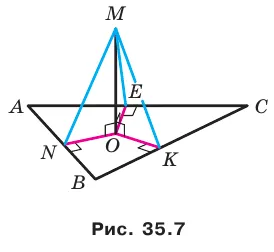
Докажите, что если точка, не лежащая в плоскости многоугольника, равноудалена от его вершин, то проекция этой точки на плоскость многоугольника является серединой его контура.
Решение:
Мы приводим доказательство для треугольника. Для других многоугольников доказательство аналогично. Предположим, что M не лежит в плоскости ABC и MA = MB = MC. Опустите перпендикуляр MO из точки M на плоскость ABC (рис. 35.3). Докажите, что O — центр окружности ABC. Правильные треугольники MOA, MOB и MOC имеют общую вершину MO и равные гипотенузы, поэтому эти треугольники равны по гипотенузе и вершине. Равенство этих треугольников означает, что O = OB = OS, то есть точка O является центром периметра треугольника ABC.
Когда необходимо определить расстояние между двумя геометрическими фигурами, делается попытка найти расстояние между ближайшими точками. Из планетометрии, например, мы знаем, что
Докажите, что если прямая параллельна плоскости, то все точки на прямой равноудалены от плоскости.
Пример:
Пусть A и B — любые две точки на прямой Точки A и B на плоскости.
Решение:
(Одна из прямых вполне может быть не параллельна самой себе, а ограничиваться параллельным смещением одной из прямых к точке пересечения с другой).
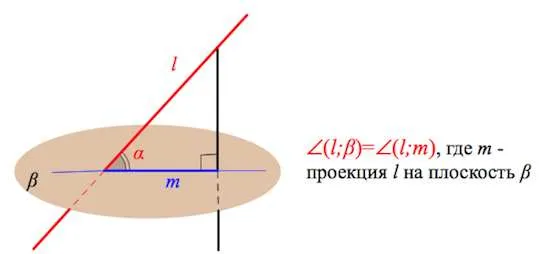
Угол между плоскостями равен углу между прямыми, которыми они пересекают любую плоскость, перпендикулярную их линии пересечения.
Этот угол не зависит от выбора такой плоскости.
Пример:
Чтобы не потерять страницу, вы можете сохранить ее для себя:
Решение:
Чтобы понять, что такое угол, образованный пересечением двух прямых, нужно вспомнить определение угла, перпендикуляра и пересечения.

Угол между скрещивающимися прямыми
Из этого определения мы должны сделать важный вывод: Величина угла в этом случае выражается любым действительным числом в интервале ( 0, 90. Если линии перпендикулярны друг другу, то угол между ними в любом случае равен 90 градусам.
Определение угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Для метода решения доступно несколько вариантов.
Угол между плоскостями
Во-первых, мы можем использовать геометрические методы. Если мы знаем что-то о дополнительных углах, мы можем соотнести их с искомым углом, используя свойства одинаковых или похожих фигур. Например, если мы знаем стороны треугольника и нам нужно вычислить угол между прямыми линиями, на которых лежат эти стороны, достаточно теоремы косинусов. Если это правильный треугольник, то полезно знать синус, косинус и тангенс угла.
Метод координат также очень полезен для решения таких задач. Давайте объясним, как правильно его использовать.
У нас есть прямоугольная (декартова) система координат O x y, с двумя прямыми. Обозначим их через a и b. Линии могут быть описаны определенными уравнениями. Исходные прямые имеют точку пересечения М. Как определить требуемый угол (обозначим его через a ) между двумя прямыми?
Начнем с основного принципа определения угла, заданного σ
- Простейшие тригонометрические неравенства
- Площадь ортогональной проекции многоугольника
- Задание №16. Досрочный ЕГЭ 2018
- Вектора. Часть 1
- Логарифмическая функция
- Прямоугольный треугольник
Угол между пересекающимися прямыми: определение, примеры нахождения
Во втором случае использовались редукционные формулы. Таким образом,
cos a cos a →, b → ^, cos a →, b → ^ ≥ 0 — cos a →, b → ^, cos a →, b → ^, cos a →, b → ^, cos a →, b → ^, cos a →, b → ^ .
Давайте выразим последнюю формулу словами:
Как найти угол между пересекающимися прямыми на плоскости
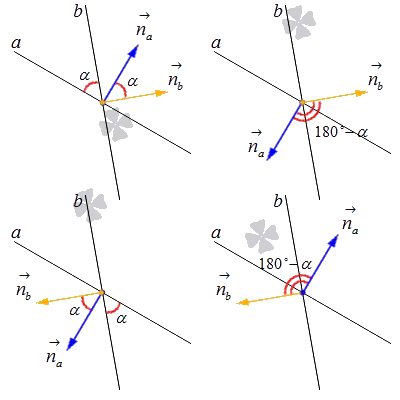
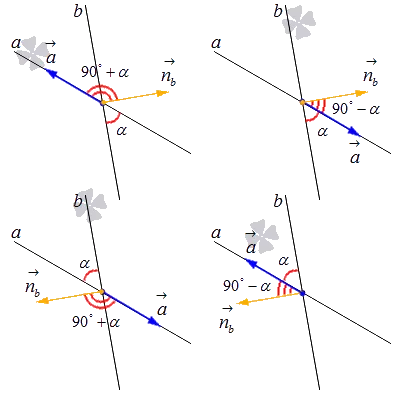
Рассмотрим последний случай — определение угла между прямыми, когда известны координаты вектора направления одной прямой и вектора нормали другой.
Предположим, что линия a имеет вектор направления a → = ( a x, a y ), а линия b имеет вектор нормали n b → = ( n b x, n b y ). Нам нужно поместить эти векторы за пределы пересечения и учесть все вариации их взаимного расположения. См. рисунок:
Вычисление такого угла можно ограничить вычислением координат направляющих векторов и определением величины угла, образованного этими векторами. Для таких примеров мы используем ту же логику, которую описали ранее.
Предположим, у нас есть прямоугольная система координат в трехмерном пространстве. Она задает две прямые a и b с точкой пересечения M. Чтобы вычислить координаты ведущих векторов, нам нужно знать уравнения этих прямых. Обозначим ведущие векторы a → = ( a x, a y, a z ) и b → = ( b x, b y, b z ). Чтобы вычислить косинус угла между ними, используем формулу
cos a = cos a →, b → ^ = a →, b → a → — b → = a x — b x + a y — b y + a z — b z a x 2 + a y 2 + a z 2 + a z 2 — b x 2 + b y 2 + b z 2
Чтобы определить сам угол, нам понадобится эта формула:
a = a r c cos a x — b x + a y — b y + a z — b z a x 2 + a y 2 + a z 2 — b x 2 + b y 2 + b z 2
- угла между направляющими векторами;
- угла между нормальными векторами;
- угла между нормальным вектором одной прямой и направляющим вектором другой.
У нас есть линия, определяемая в трех измерениях уравнением x 1 = y — 3 = z + 3 — 2, которая, как известно, пересекает ось O z. Вычислите угол пересечения и косинус этого угла.
Решение
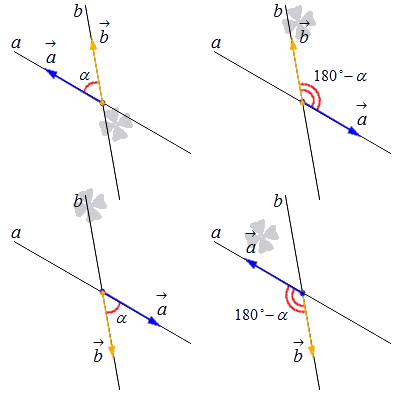
Если угол между двумя векторами не является тупым, то он и будет нужным нам углом между пересекающимися прямыми a и b. Если же он тупой, то искомый угол будет равен углу, смежному с углом a →, b → ^. Таким образом, α = a →, b → ^ в том случае, если a →, b → ^ ≤ 90 °, и α = 180 ° — a →, b → ^, если a →, b → ^>Обозначим вычисляемый угол через α. Напишите координаты вектора директрисы для первой строки — a → = ( 1, — 3, — 2 ). В качестве направляющего вектора для оси приложения можно взять координатный вектор k → = ( 0, 0, 1 ). Мы получили необходимые данные и можем вставить их в нужную формулу:
Исходя из того, что косинусы равных углов равны, мы можем переписать получившиеся равенства так: cos α = cos a →, b → ^, если a →, b → ^ ≤ 90 ° ; cos α = cos 180 ° — a →, b → ^ = — cos a →, b → ^, если a →, b → ^>Обозначим вычисляемый угол через α. Напишите координаты вектора директрисы для первой строки — a → = ( 1, — 3, — 2 ). В качестве направляющего вектора для оси приложения можно взять координатный вектор k → = ( 0, 0, 1 ). Мы получили необходимые данные и можем вставить их в нужную формулу:
Отсюда следует, что искомый угол a r c cos 1 2 = 45°.
Ответ: cos a = 1 2, a = 45°.<0 ⇔ cos α = cos a →, b → ^
Чтобы получить доступ к этому и другим видеоурокам из комплекта, вам необходимо добавить его в свой личный кабинет.
2. Распределите видеоуроки по личным кабинетам ваших учеников.
— Исследуйте углы между линиями, которые пересекаются и скрещиваются в пространстве.
Как вычислить угол между пересекающимися прямыми в пространстве
Напомним, что два луча O и O.
в пространстве, не лежащие на одной прямой, считаются смежными, если они параллельны и лежат в той же полуплоскости, что и граница O
. Если стороны двух углов конгруэнтны друг другу, то эти углы равны.
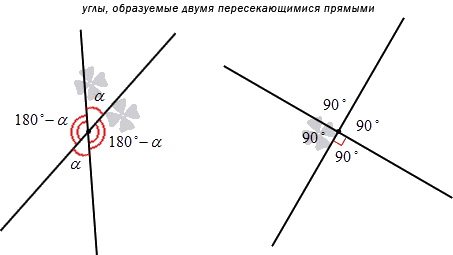
Как вы уже знаете, две пересекающиеся прямые лежат в одной плоскости и образуют четыре несократимых угла. Если один из этих углов известен, мы можем определить остальные три угла.
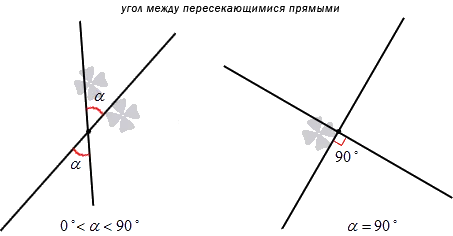
Определение. Если пересекающиеся прямые образуют тупой и острый углы, то углом между этими прямыми будет тот, который не больше одного из трех других углов, то есть меньший из двух углов.
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен девяноста градусам.
Пусть a — угол, который не больше любого из трех других углов. Тогда мы говорим, что угол между пересекающимися прямыми равен α. Очевидно, что угол альфа между двумя пересекающимися прямыми удовлетворяет условию:
Теперь введем понятие угла между пересекающимися прямыми. Предположим, у нас есть две пересекающиеся прямые a и b. Возьмем любую точку M
в пространстве и через него линии A
проходят параллельно прямым a и b соответственно.
Тогда угол между пересекающимися прямыми a и b является углом между одновременными прямыми A .
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
. То есть, если угол между линиями A .
равен φ, то мы говорим, что угол между пересекающимися прямыми a и b равен φ.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Угол между прямыми»
Докажем, что угол между двумя пересекающимися прямыми не зависит от выбора точки M
Возьмем любую другую точку M1A1и через него линии a1и б
параллельны a и b соответственно. Пусть угол между прямыми a
и б
быть
и угол между линиями a
и б1один1B1Если линии a

лежат в одной плоскости, то по свойству углов пересечения для параллельных прямых угол α1B1равна φ и равна углу a.1B1Пусть теперь линии a
и б1.
которые пересекаются в точке M2лежат в одной плоскости. И пусть линии2и б2которые пересекаются в точке M1и б1Поскольку линия a1параллельна прямой a и прямой a2и б2Поскольку линия a2.
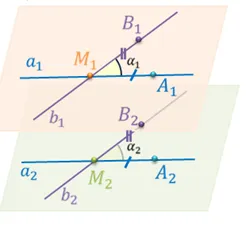
также параллельны. Поскольку линия b1, b1, a2, b2параллельна прямой b и прямой b1параллельна прямой b, то согласно принципу параллельности прямых в пространстве, прямые b2.
и б1и б1Давайте вместе ликвидируем пробел в знаниях. Наши специалисты будут рады помочь вам! Первый вводный урок бесплатный!1Отличный преподаватель, который всегда предан ученикам и заботится об их успехе. Его интересно слушать и с ним интересно работать!2и б2Давайте вместе ликвидируем пробел в знаниях. Наши специалисты будут рады помочь вам! Первый вводный урок бесплатный!2Мне очень понравилось учиться у Андрея Юрьевича. Я впервые встречаю учителя, который, прежде чем преподавать язык, рассказывает о его происхождении — географии, культуре и истории. Я очень ценю такой подход. Видно, что преподаватель очень опытный. Я очень довольна своим первым уроком! Я буду продолжать учиться у этого преподавателя.
Ответственный, настойчивый, харизматичный, последовательный, очень хороший уровень подготовки, терпеливый. Наша дочь очень довольна и, очевидно, Intere1Большое спасибо. Я очень рада, что мы нашли этот источник для обучения. Ирина Сергеевна объясняет все быстро, четко и динамично. Всего за несколько уроков мы наверстали упущенную химию и продвинулись вперед. Мы обязательно обратимся снова в будущем.2Елизавета делает хорошие успехи и учится с радостью и энтузиазмом. Римма Николаевна очень интересно преподносит материал. Мне очень нравится этот учитель, мы очень довольны уроками.1Нам нравилась Нина Ивановна, хороший человек и прекрасный учитель. Она очень ответственная, трудолюбивая и знающая. Она сразу же нашла подход к своему ученику. Она может доходчиво объяснить любую тему. Учитель, в отличие от многих других преподавателей, не тратит время впустую, а действительно помогает.2Она была прекрасным преподавателем и нашла подход с первых же уроков. Она объяснила все очень четко и понятно. Моему ребенку она очень нравится, и он просит о дополнительных занятиях.1Здравствуйте, Рита Ивановна очень профессионально оценила все пробелы в знаниях моего сына, и мы бы с удовольствием продолжили обучение с ней! Уроки очень хорошие, преподаватель все понятно объясняет, я рекомендую ее всем.2Спасибо, Ольга Ольга, за урок на каникулах. Желаю ей здоровья и благополучия, побольше счастливых событий в жизни, процветания, успехов и удачи в ее нелегком и нужном труде. Спасибо за урок, мне он очень понравился!1и б2








