Что такое корень уравнения. Что такое корень уравнения?

Пусть x — площадь самого маленького шкафа. Тогда вторая комната занимает площадь 3x. Его общая площадь составляет 508 м². Это условие может быть представлено следующим уравнением:

Корни квадратного уравнения

Типы корней квадратного уравнения. Рассматриваются вещественные, кратные и комплексные корни. Разложение на кратные квадратичные триномы. Геометрическая интерпретация. Примеры определения корня и факторизации.

Рассмотрим квадратное уравнение: (1). Корни квадратного уравнения (1) даются следующими формулами: ?. Эти формулы можно объединить следующим образом: Если известны корни квадратного уравнения, то многочлен второй степени можно представить в виде произведения коэффициентов (разложенных на множители): .

Тогда предположим, что — действительные числа. Рассмотрим мощность дискриминанта квадратного уравнения: Если дискриминант положительный, то квадратное уравнение (1) имеет два различных действительных корня: ? Тогда эволюция квадратичного тринома по факторам выглядит следующим образом:. Если мощность дискриминанта равна нулю, то квадратное уравнение (1) имеет два кратных (одинаковых) действительных корня:. Разложение на множители:. Если мощность дискриминанта отрицательна, то квадратное уравнение (1) имеет два комплексно сопряженных корня: ? Здесь мнимая единица, ? и действительная и мнимая части корней: ? Затем

Графическая интерпретация

Если построить график функции, который представляет собой параболу, то пересечения графика с осью являются корнями уравнения. Если, то график пересекает ось расстояний (the ) в двух точках (см. рисунок ⇓). Если, то график пересекает ось бездны в одной точке (см. рисунок ⇓). Если, то график не касается оси пропасти (см. рисунок ⇓).

Выполните преобразования и примените формулы (f.1) и (f.3): где ; .

Таким образом, получаем формулу для полинома второй степени в виде: Таким образом, мы видим, что уравнение справедливо для и, то есть и и являются корнями квадратного уравнения.

Примеры определения корней квадратного уравнения

Пример 1

Найдите корни квадратного уравнения: (1.1) .

Запишем квадратное уравнение в общем виде: Сравнение с уравнением (1.1) дает значения коэффициентов: Найдите дискриминант: Поскольку дискриминант положительный, уравнение имеет два действительных корня: ; ; ; ; .

Разложение квадратичного тринома на коэффициенты дается.

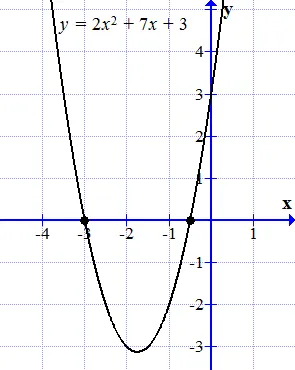
Постройте график функции. Графиком этой функции является парабола. Она пересекает ось расстояния (ось ) в двух точках: и. Эти точки являются корнями исходного уравнения (1.1).

Пример 2

Найдите корни квадратного уравнения: (2.1) .

Запишите квадратное уравнение в общем виде: Сравните с исходным уравнением (2.1), чтобы найти коэффициенты: Найдите дискриминант: поскольку дискриминант равен нулю, уравнение имеет два кратных (одинаковых) корня: ? .

Разложение тринома на множители выглядит следующим образом.

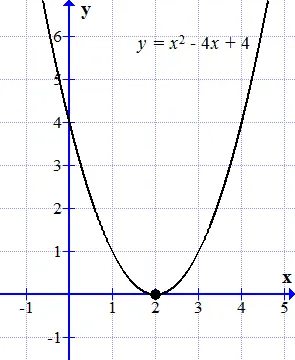
Построим график функции. Графиком этой функции является парабола. Она касается оси дивергенции (оси ) в одной точке: эта точка является корнем исходного уравнения (2.1). Поскольку этот корень дважды входит в расширение: такой корень называется многообразием. Поэтому предполагается, что существует два одинаковых корня: .

Пример 3

Найдите корни квадратного уравнения: (3.1) .

Запишем квадратное уравнение в общем виде: (1). Перепишем исходное уравнение (3.1): Сравните его с (1) и найдите коэффициенты: Найдите дискриминант:. Дискриминант отрицательный, т.е. вещественных корней нет.

.

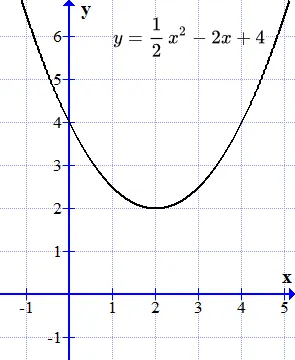
Постройте график функции. Графиком функции является парабола. Она не пересекает ось расстояния (ось ), поэтому действительных корней нет.

Настоящих корней нет. Корни сложные: ; ; ; ; ; ; ; …

Автор: Олег Одинцов. Опубликовано: 19-04-2016

Понятие уравнения

Уравнения являются одним из фундаментальных понятий алгебры и всей математики. Сам термин «алгебра» происходит от названия книги «Китаб аль-джебрвал-мукабала», написанной великим ученым аль-Хорезми в 830 году, в которой он анализировал способы решения уравнений.

Уравнение — это своего рода равенство. Он должен содержать как минимум одну переменную, но количество переменных может быть любым. Давайте определим понятие уравнения:

Следующие уравнения являются примерами уравнений:

• x=5;
• a+b+c=9;
• dg+98=(j+f)·k;
• L²+V²= 25²;
• 5z+3z=100.

Во всех приведенных выше примерах мы можем заменить переменные вещественными числами, но в старших классах вводятся более сложные уравнения, где в качестве переменных выступают такие математические объекты, как функции и векторы.

Уравнения — это не просто абстрактные математические конструкции. Они часто встречаются, когда мы описываем окружающий нас мир на формальном языке математики. Предположим, что ежемесячный доход семьи обозначается буквой D, а расходы — буквой P. Разница между доходами и расходами семьи — это сбережения (C). Формально эта ситуация может быть описана уравнением:

Что такое корень уравнения?

Как и в любом выражении с буквой, в уравнение можно подставлять различные значения переменных. В зависимости от этого оно преобразуется либо в истинное, либо в недопустимое уравнение. Подставьте r=6 в уравнение

и получаем обозначение

Очевидно, что это уравнение истинно. Однако если мы положим r=1, то получим недопустимое уравнение

Число 6 является корнем уравнения (r+2)-r=48, а число 1 — нет.

Давайте точно определим понятие корня уравнения:

Слово «количество» используется для определения уравнения с более чем одной переменной. Итак, есть две переменные, нам нужно определить пару чисел, которые могут окружать выражение в равенстве. Так, для уравнения

корнем является величина M=4; W=6. Однако, если рассматривать по отдельности, то ни число 6, ни число 4 не являются корнями уравнения.

Цель решения уравнений — найти корни уравнения:

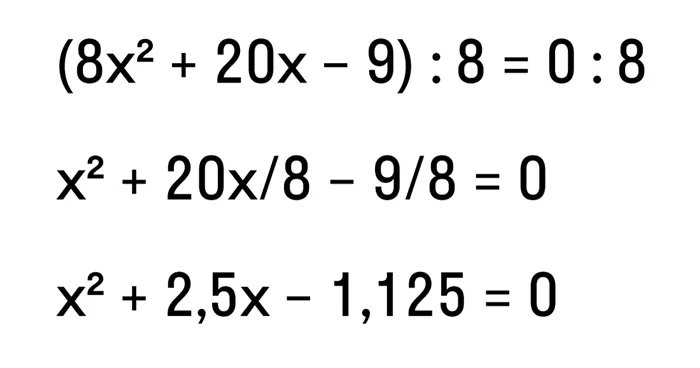
Возникает вопрос: сколько корней может иметь уравнение? Число может быть совершенно другим. Можно написать уравнение, которое имеет любое количество корней. Мы покажем вам, как это сделать. Уравнение

имеет ровно один корень, равный единице. Теперь умножьте левую часть на выражение (y-2):

Произведение нескольких чисел может быть нулевым только в том случае, если хотя бы одно из них равно нулю. Значит, корнями этого уравнения являются числа 1 и 2. Чтобы составить уравнение с тремя корнями, добавьте к левой части еще одно выражение в скобках:

Теперь у нас есть три корня: 1, 2 и 3. Если вы добавите аналогичные выражения в левой части

В этом случае, однако, следует отметить, что количество корней может зависеть от того, какие числа можно подставлять в письменное выражение. Дело в том, что в 16 веке математики изобрели новое понятие — «мнимые числа». Их особенность в том, что при умножении на себя они дают отрицательное число! Например, число «мнимая единица», обозначаемое символом i, в квадрате равн о-1:

Мнимые числа были введены в алгебру специально для того, чтобы иметь возможность извлекать квадратный корень из отрицательных чисел. Однако со временем спектр их применения в математике значительно расширился. Более того, на практике используются даже мнимые числа. Оказалось практичным использовать их для описания процессов в электрических цепях и квантовых явлений. Воображаемые числа рассматриваются более подробно в старших классах средней школы и в университете. Сначала мы рассматриваем только вещественные корни уравнений.

Иногда уравнение формулируется таким образом, что некоторые числа нельзя подставить. Часто это связано с недопустимостью деления на ноль. Таким образом, уравнение

Рассмотрим простое уравнение вида

где z — переменная, а b — любое действительное число. Ниже приведены примеры простейших уравнений:

Очевидно, что единственным корнем уравнения z=b является число b.

Решение уравнений с одной переменной

Чтобы решить все остальные уравнения, их упрощают шаг за шагом, сводя к одному или нескольким простым уравнениям. Для этого из исходного уравнения, применяя ряд правил, получают эквивалентное или равноценное уравнение.

Например, уравнения 2y+5=15 и 4z=20 эквивалентны друг другу, так как имеют один корень, равный 5:

Каковы возможности получения другого уравнения, эквивалентного этому? Во-первых, и левая, и правая части уравнения могут быть решены с помощью стандартных алгебраических процедур:

Например, обозначение 5d+4d=5z+5k будет соответствовать уравнению 9d=5(z+k). Здесь мы складываем аналогичные суммы в левой части и в правой части получаем коэффициент 5 из скобок:

Во-вторых, к левой и правой частям можно добавить любое эквивалентное выражение. Уравнения y+9=10 и y+10=11 будут равны, так как обе части увеличены ровно на единицу:

Однако выражения, содержащие переменные, также могут быть дополнены, так что уравнения r+6=8 и r+6+r²=8+r² будут эквивалентны друг другу.

• складывать подобные слагаемые;
• раскрывать скобки;
• выносить общий множитель за скобки.

Однако здесь можно допустить логическую ошибку, если забыть определения уравнений. Вот пример. Уравнение

имеет единственный корень, равный 2:

Теперь добавьте выражение 1/(N-2) к его частям:

Подумайте, сколько решений имеет полученное уравнение? Оказалось, что у него их нет! Установите

3d ²-2d² = 10-7 (сдвинуть 2d² влево),

d² = 3 (сложите аналогичные суммы).

Другой пример:

4F-9+2G+2F = 5+2G (сдви г-2F влево),

4F+2F = 5+2G+9-2G (сдвиньт е-9 и 2G вправо),

2F = 14 (добавьте аналогичные суммы).

В-третьих, обе части уравнения можно умножить или разделить на одно и то же число или выражение. Поэтому уравнения 3p=7 и 6p=14 эквивалентны:

Но здесь стоит быть осторожным и рассмотреть диапазоны определений уравнений. Вот пример ошибки. Уравнение

Это правило подходит, когда вы уже вычислили все неизвестные и известные, но перед переменной еще есть коэффициент. Чтобы избавиться от нежелательного коэффициента, примените правило уменьшения или увеличения коэффициента уравнения несколько раз.

Возьмем пример: решите уравнение 5x=20.

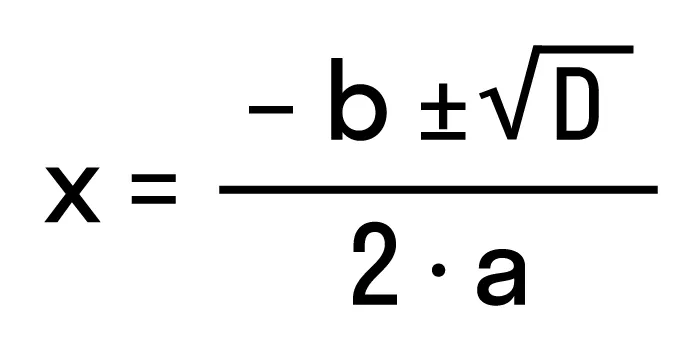
Решение. Однако нам мешает сделать это фактор 5, который стоит перед переменной x. Нам не нужно перемещать цифры или фигуры. Мы не можем просто перенести их в правую часть уравнения, потому что между числом 5 и переменной x находится множитель 5⋅x. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы сдвинуть 5 вправо. Но мы не можем этого сделать. Однако мы можем уменьшить все уравнение в 5 раз или разделить на 5. Убедитесь, что вы разделили правую и левую стороны одновременно.

5x = 20 5x :5 = 20 :5 :5 5:5x = 4 1x = 4 или x = 4

Проверьте уравнение. Подставьте 4 вместо x. 5x=20 5⋅ 4 =20 20 20=20 мы имеем верное равенство, корень уравнения верен. Ответ: x=4.

Рассмотрим следующий пример: найдите корни уравнения.

Решение: Поскольку переменной x предшествует коэффициент, этот коэффициент нужно убрать. Нам нужно увеличить все уравнение в 3 раза или умножить на 3. Убедитесь, что вы перемножили левую часть уравнения и правую часть.

Давайте проведем проверку уравнения. Замените переменную x на полученный корень уравнения 21.

7=7 — правильное уравнение.

Ответ: Корнем уравнения является x=21.

Следующий пример: Найдите корни уравнения.

Решение: Сначала переместит е-1 в правой части уравнения относительно знака равенства и в левой части, их знаки поменяются местами. Теперь нам нужно умножить все уравнение на 5, чтобы вычесть 5 из знаменателя коэффициента перед переменной x. Теперь нам нужно умножить все уравнение на 5, чтобы вычесть 5 из знаменателя перед переменной x.

Правила уменьшения или увеличения уравнения в несколько раз.

Затем все уравнение делится на 3.

3x :3 =45 :3 (3:3)x=15

Давайте проведем тест. Подставьте найденный корень в уравнение.

Чтобы подвести итог рассмотренной нами теме уравнений, давайте рассмотрим общие правила решения уравнений:

Эти правила применимы ко всем типам уравнений (линейные, квадратичные, логарифмические, тригонометрические, логические, иррациональные, экспоненциальные и другие типы). Поэтому важно понять эти простые правила и научиться их применять.

Отменить ответ

Вы должны войти в систему, чтобы оставить комментарий.

Пожалуйста, отключите блокировку рекламы или добавьте сайт в исключения блокировки, если вы хотите, чтобы проект развивался.

Как мы уже знаем, существует три типа неполных квадратных уравнений:

Давайте рассмотрим шаг за шагом, как решать неполные квадратные уравнения с помощью

Пример 1. Решите задач у-6x 2 = 0.

Рассмотрим неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Давно известно, что слагаемые в уравнениях носят двусторонние пиджаки: если мы переносим их из одной части уравнения в другую, они натягивают пиджак на другую сторону — меняют знак на противоположный.

Мы также знаем, что если разделить обе части уравнения на одно и то же число (отличное от нуля), то получится уравнение. Это одно и то же, только с разными цифрами.

Помня все это, давайте решим неполное квадратное уравнение (делаем «равносильные преобразования»): ax 2 + c = 0:

Вот и все, теперь мы готовы найти корни неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/a может быть отрицательным или положительным. Давайте рассмотрим конкретные случаи.

Как решать уравнения? Алгоритм действий.

0, то корни уравнения x 2 = — c/a различны. Например, мы можем применить правило квадратного корня. Тогда корнем уравнения является число √- c/a, так как (√- c/a) 2 = — c/a. Альтернативно, корнем уравнения может быть также -√- c/a, так как (-√- c/a) 2 = — c/a. Да, уравнение не имеет других корней.

1. Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
2. Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
3. Избавиться от коэффициента при переменной если нужно.
4. В итоге всех действий получаем корень уравнение. Выполняем проверку.

Неполное квадратное уравнение ax 2 + c = 0 эквивалентно уравнению x 2 = -c/a, которое:

You may also like:

Деление рациональных чисел примеры и правила.

Нужен репетитор по математике (алгебре) или геометрии?

Умножения рациональных чисел, математика, примеры.

Сложение рациональных чисел, правила и примеры.

Добавить комментарийПример 1: Найдите решение уравнения 8x 2 + 5 = 0.

Ответ: Уравнение 8x 2 + 5 = 0 не имеет корней.

Свежие записи

Третий тип неполного квадратного уравнения все еще требует решения, когда c = 0.

Решение неполных квадратных уравнений

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом факторизации. Как проанализировать квадратное уравнение:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Для нахождения результата квадратного уравнения была разработана формула корней. Это выглядит примерно так:

Как решить уравнение ax 2 = 0

Где D = b 2 — 4ac — дискриминант квадратного уравнения.

Это обозначение означает:

Чтобы легко использовать эту формулу, необходимо понять, как она была выведена. Давайте подойдем к концу этой темы.

Теперь мы знаем, что при решении квадратных уравнений можно использовать универсальную формулу корней — она помогает находить комплексные корни.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так: −6x 2 = 0 x 2 = 0 x = √0 x = 0

Как решить уравнение ax 2 + с = 0

На уроках алгебры в 8 классе вам может понадобиться найти действительные корни квадратного уравнения. Для этого важно найти дискриминант и убедиться, что он не отрицателен, прежде чем применять формулы, и только потом вычислять значения корней. Если дискриминант отрицательный, то уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Чтобы запомнить алгоритм решения квадратных уравнений и использовать его с легкостью, давайте потренируемся!

• перенесем c в правую часть: ax 2 = — c,
• разделим обе части на a : x 2 = — c/а.

Мы уже знаем, как решать квадратные уравнения, теперь нам просто нужно закрепить наши знания на практике.

Если — c/а>Пример 1. Решите уравнени е-4x 2 + 28x — 49 = 0.

Ответ: Единственный корень — 3,5.

Пример 2. Решите уравнение 54 — 6x 2 = 0.

1. Перенесем свободный член в правую часть: 8x 2 = — 5
2. Разделим обе части на 8: x 2 = — 5/8
3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

= 3, х

Как решить уравнение ax 2 + bx = 0

Реакция:

Пример: Нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдите корни по известной нам формуле. Вычислите дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставьте формулу для корней:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x .
2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Дискриминант: формула корней квадратного уравнения

Для простоты обозначим выражение n 2-ac как D

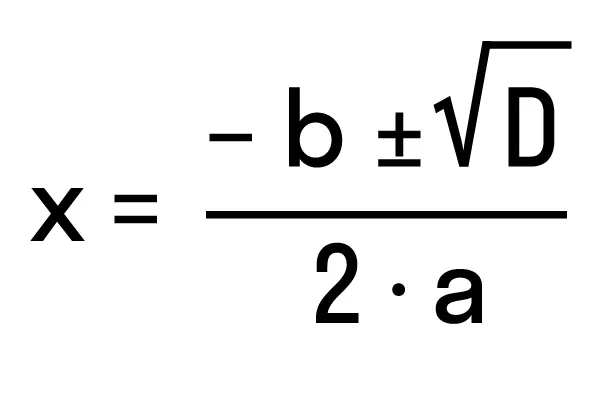
. Тогда формула для корней квадратного уравнения со вторым коэффициентом 2-n имеет вид

где D

= n 2 — ac.

Алгоритм решения квадратных уравнений по формулам корней

Внимательные наблюдатели уже заметили, что D = 4D

или D

= D/4. Простыми словами: D

• вычислить его значение дискриминанта по формуле D = b 2 −4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

— составляет четверть разделительной мощности. И оказывается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Примеры решения квадратных уравнений

Давайте сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n

1. Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень х = — 28/2(-4) х = 3,5

1. Произведем равносильные преобразования. Умножим обе части на −1 54 — 6x 2 = 0 | *(-1) 6x 2 — 54 = 0
2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую 6x 2 = 54 х 2 = 9 х = ±√9 х₁₂= — 3

1. Преобразуем уравнение так, чтобы появились множители х(х — 1) = 0 х₁ = 0, х₂ = 1

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую x 2 — 10 = 39 x 2 = 39 + 10 x 2 = 49 х = ±√49 х₁ = 7, х₂ = −7

1. Найдем дискриминант по формуле D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
2. Дискриминант отрицательный, поэтому корней нет.

Формула корней для четных вторых коэффициентов

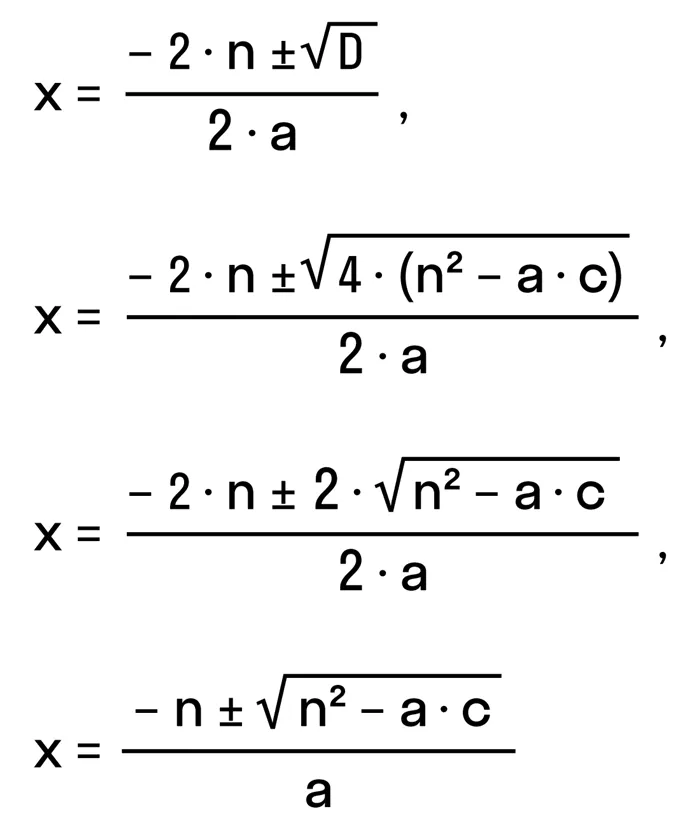
₁

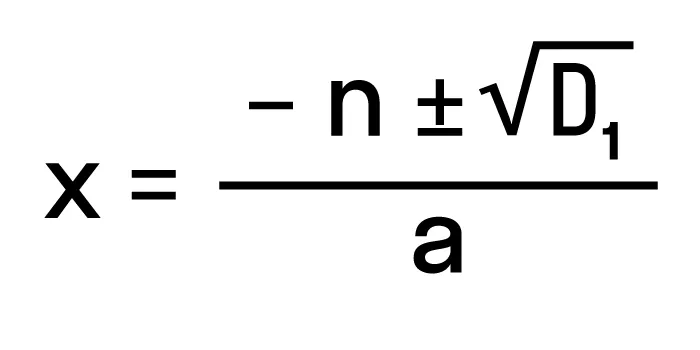
₁

₁₁₁

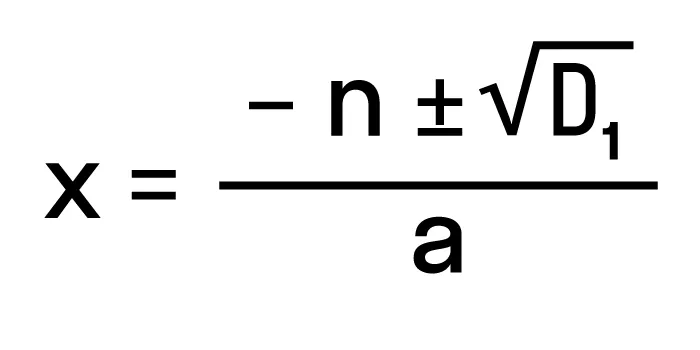
• вычислить D₁= n 2 — ac;
• если D₁<0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁>0, значит можно найти два действительных корня по формуле