Что такое площадь в математике. Что такое площадь в математике?

Формула площади прямоугольника от двух его сторон и угла между ними Площадь прямоугольника равна произведению длин его сторон и синуса угла между ними.

Как найти площадь фигуры

В геометрии фигура определяется как ряд точек на плоскости, часть плоскости или криволинейная поверхность, ограниченная со всех сторон. В реальной жизни нас окружает множество предметов, которые можно назвать формами: мобильный телефон, холодильник, летающий змей. В этой статье вы узнаете, как найти площадь различными способами.

— Обновление 21 октября 2022 года

Обозначение площади

Площадь — это атрибут замкнутой геометрической фигуры, который дает информацию о ее размере. S (квадрат) — это знак площади.

Если параметры фигуры находятся в разных единицах длины, мы не сможем решить ни одной задачи. Поэтому для правильного решения задачи все данные должны быть преобразованы в единую единицу измерения.

Общие единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Выясните, в каких темах вы «хромаете», а затем справьтесь с ними без заучивания формул и скучных лекций.

Круг

Круг — это множество точек плоскости, ограниченных окружностью, радиус которой равен расстоянию от центра. Радиус обычно определяется как расстояние между центром и любой точкой окружности.

1. S = π × r 2, где r — это радиус, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
2. S = &pi × d 2 : 4;, где d — это диаметр.
3. S = L 2 ​ : (4 × π), где L — это длина окружности.

Вам нужно быстро подтянуть свои знания перед экзаменом? Запишитесь на курсы ЕГЭ по математике в Skysmart!

Характеристики понятия

Район имеет несколько особенностей:

• Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.
• Нормируемость .

На практике площадь можно определить с помощью палки или специального измерительного прибора — планиметра.

Площади простых фигур

Формула для определения площади зависит от формы. Название района в большинстве случаев остается неизменным — это латинская заглавная буква «S». Это не правило, а лишь одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах эта область может обозначаться другими буквами.

Рассмотрим наиболее распространенные формулы для определения регионов:

• Прямоугольник. S=a*b – произведение длины на ширину.
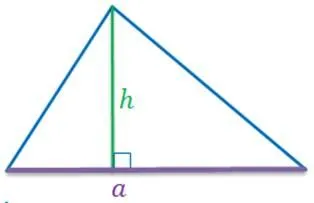
• Треугольник. $S=<1\over2>a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
• Круг. $S=\pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.

Сначала необходимо убедиться, что параметры формы имеют одинаковые единицы измерения. Например, если ширина прямоугольника указана в миллиметрах, а длина — в сантиметрах, необходимо преобразовать сантиметры в миллиметры и только после этого использовать формулу.

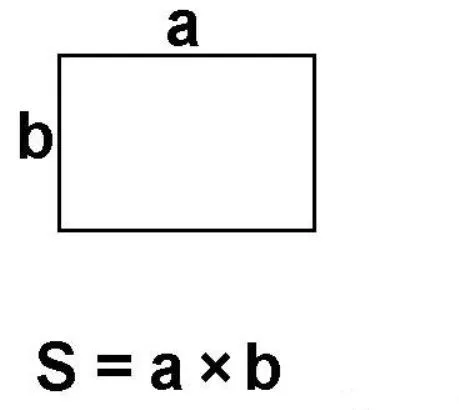
Какова площадь квадрата? Это сторона фигуры, которая поднимается, образуя квадрат. Это объясняется тем, что квадрат — это прямоугольник, длина и ширина которого равны:

Если длина стороны квадрата составляет 100 метров, то его площадь равна одному гектару. Эта единица используется, когда необходимо оценить размер земельной площади при распределении сельскохозяйственных угодий:

Поля также могут быть измерены в арсах, обычно называемых «цельсиями», d

Площадь произвольной фигуры

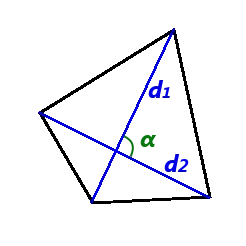
Формула площади четырехугольника от длины его диагоналей и угла между ними Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними:

Где S — площадь четырехугольника, d

Формулы площади ромба

, d

— длины диагоналей четырехугольника, a — угол между диагоналями четырехугольника.

Формула для площади окружности (на основе длины окружности и радиуса эндоцикла) Площадь выпуклого четырехугольника равна произведению полуокружности и радиуса эндоцикла.

Формулы площади выпуклого четырехугольника

Формула для площади четырехугольника с длинами сторон и значениями противоположных углов

Площадь прямоугольника, которая может быть описана кругом₁Формула для определения площади зависит от формы. Название района в большинстве случаев остается неизменным — это латинская заглавная буква «S». Это не правило, а лишь одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах эта область может обозначаться другими буквами.₂Рассмотрим наиболее распространенные формулы для определения регионов:

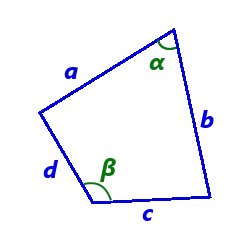
Рисунок 1. Высота в произвольном треугольнике.

В следующем примере необходимо следить за тем, чтобы параметры рисунка были в одних и тех же единицах измерения. Например, если ширина прямоугольника указана в миллиметрах, а длина — в сантиметрах, необходимо преобразовать сантиметры в миллиметры и только после этого использовать формулу.

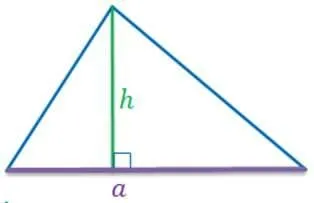
Рисунок 2. Площадь прямоугольника.

Площади простых фигур

Формула для определения площади зависит от формы. Название района в большинстве случаев остается неизменным — это латинская заглавная буква «S». Это не правило, а лишь одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах эта область может обозначаться другими буквами.

Рассмотрим наиболее распространенные формулы для определения регионов:

• Прямоугольник. S=a*b – произведение длины на ширину.
• Треугольник. $S=a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
• Круг. $S=pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.

Поля также могут измеряться в арсах, обычно называемых «сантиметрами», поскольку ар — это квадрат с длиной стороны 10 метров и площадью 100 $m^2$ каждый.

Сначала необходимо убедиться, что параметры формы имеют одинаковые единицы измерения. Например, если ширина прямоугольника указана в миллиметрах, а длина — в сантиметрах, необходимо преобразовать сантиметры в миллиметры и только после этого использовать формулу.

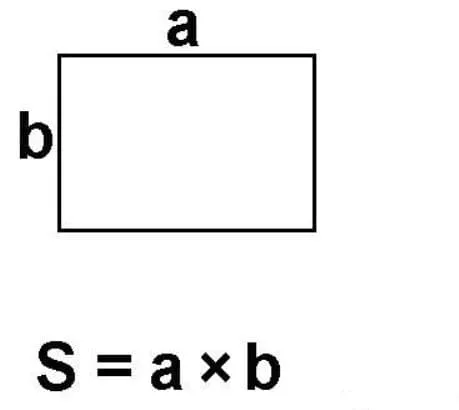
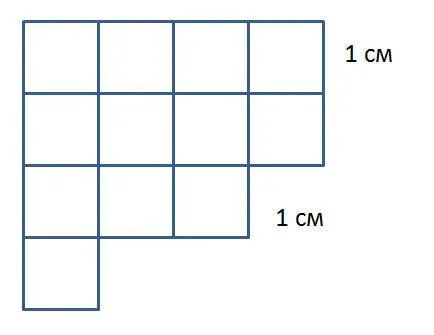
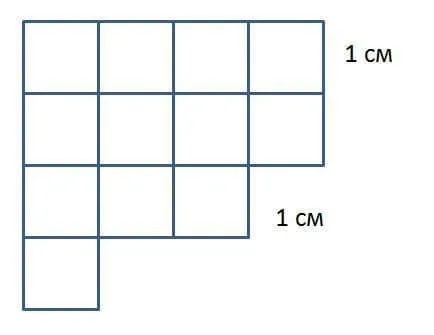
Рисунок 3. Область сложной формы.

Какова площадь квадрата? Это сторона фигуры, которая поднимается, образуя квадрат. Это объясняется тем, что квадрат — это прямоугольник, длина и ширина которого равны:

Если длина стороны квадрата составляет 100 метров, то его площадь равна одному гектару. Эта единица используется, когда необходимо оценить размер земельной площади при распределении сельскохозяйственных угодий:

Поля также могут быть измерены в арсах, обычно называемых «цельсиями», d

Площадь произвольной фигуры

Формула площади четырехугольника от длины его диагоналей и угла между ними Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними:

Если длина стороны квадрата составляет 100 метров, то его площадь равна одному гектару. Эта единица используется, когда при распределении сельскохозяйственных земель необходимо оценить размер участка:

Где S — площадь четырехугольника, d

Характеристики понятия

Район имеет несколько особенностей:

• Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.
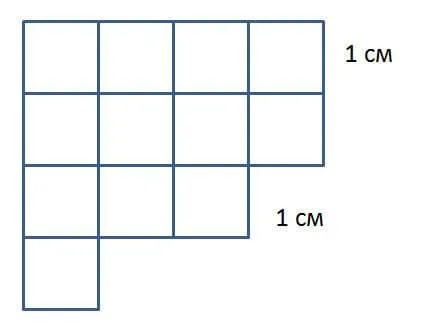
• Нормируемость. Что это значит? Это значит, что у площади есть какая-то норма, с которой и сравнивают поверхность любой фигуры. Норма площади это квадрат со сторонами 1 на 1. Если это квадрат со сторонами 1 на 1 см, то единица измерения площади будет называться см квадратный и т.д.
• Если две фигуры объединить, так, что они не будут иметь общих внутренних точек, то есть совместить фигуры по какой-либо стороне, то площадь получившейся фигуры будет равна сумме площадей двух изначальных фигур.

На практике площадь можно определить с помощью палки или специального измерительного прибора — планиметра.

Площади простых фигур

Формула для определения площади зависит от формы. Название района в большинстве случаев остается неизменным — это латинская заглавная буква «S». Это не правило, а лишь одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах эта область может обозначаться другими буквами.

Рассмотрим наиболее распространенные формулы для определения регионов:

• Прямоугольник. S=a*b – произведение длины на ширину.
• Треугольник. $S=a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
• Круг. $S=pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.

Поля также могут измеряться в арсах, обычно называемых «сантиметрами», поскольку ар — это квадрат с длиной стороны 10 метров и площадью 100 $m^2$ каждый.

Сначала необходимо убедиться, что параметры формы имеют одинаковые единицы измерения. Например, если ширина прямоугольника указана в миллиметрах, а длина — в сантиметрах, необходимо преобразовать сантиметры в миллиметры и только после этого использовать формулу.

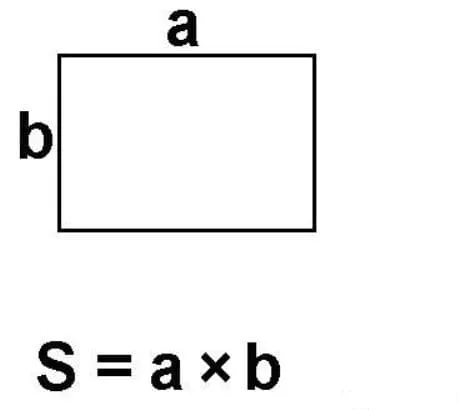
Рисунок 3. Область сложной формы.

Какова площадь квадрата? Это сторона фигуры, которая поднимается, образуя квадрат. Это объясняется тем, что квадрат — это прямоугольник, длина и ширина которого равны:

Если длина стороны квадрата составляет 100 метров, то его площадь равна одному гектару. Эта единица используется, когда необходимо оценить размер земельной площади при распределении сельскохозяйственных угодий:

Поля также могут быть измерены в арсах, обычно называемых «цельсиями», d

Площадь произвольной фигуры

Формула площади четырехугольника от длины его диагоналей и угла между ними Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними:

Если длина стороны квадрата составляет 100 метров, то его площадь равна одному гектару. Эта единица используется, когда при распределении сельскохозяйственных земель необходимо оценить размер участка:

Где S — площадь четырехугольника, d