Вертикальные линии — определение и свойства
Что такое прямые углы?
Следствия теоремы Виета
Работа с формулами в задаче B12
Пример решения задачи 15
Задача B15: частный случай квадратичных функций
Биссектриса угла
Сегодня это будет очень простой урок. Мы рассмотрим один объект, биссектрису угла, и докажем его самое важное свойство, которое пригодится нам в будущем.
Сохраняйте спокойствие: иногда ученики, которые хотят получить хорошую оценку на том же ЕГЭ или GCSE, не могут даже правильно выучить определение биссектрисы угла на первом уроке.
И вместо того, чтобы заниматься действительно интересными проблемами, мы тратим время на такие простые вещи. Так что читайте, смотрите — а потом принимайтесь за дело 🙂
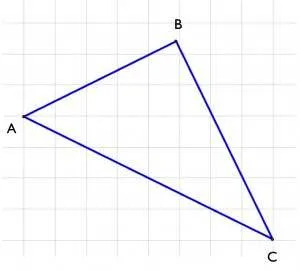
Во-первых, несколько странный вопрос: что такое угол? Правильно: угол состоит из двух лучей, исходящих из одной точки. Например:
Как вы видите на рисунке, углы могут быть острыми, тупыми или прямыми — сейчас это не имеет значения. Для простоты на каждом луче часто ставят дополнительную точку и говорят, что это угол $AOB$ (записывается как $\угольник AOB$).
Гауптман Очевидность предполагает, что, кроме лучей $OA$ и $OB$, из точки $O$ всегда может исходить множество лучей. Среди них, однако, есть особая форма, называемая дихотомической.
Определение: — это луч, исходящий из вершины угла и рассекающий угол.
Для указанных углов биссектрисы имеют следующий вид:
Поскольку на реальных чертежах не всегда очевидно, что луч (в нашем случае это луч $OM$) делит исходный угол на два равных угла, в геометрии принято обозначать равные углы одинаковым количеством дуг (на нашем чертеже это одна дуга для острого угла, две — для тупого, три — для прямого).
Хорошо, мы изменили определение. Теперь нам нужно понять свойства биссектрисы угла.
Основное свойство биссектрисы угла
Биссектриса угла действительно обладает многими свойствами. Мы рассмотрим их в следующем уроке. Но есть одна вещь, которую вы должны понять сейчас:
Множество — это геометрическое расположение точек, которые равноудалены от сторон заданного угла.
В математических терминах это означает, что два факта существуют одновременно:
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте проясним один момент: Что такое расстояние между точкой и стороной угла? Здесь мы имеем старомодное определение расстояния точки от прямой:
Определение: — это длина перпендикуляра, проведенного из данной точки к данной прямой.
Например, рассмотрим прямую $l$ и точку $A$, которая не лежит на этой прямой. Проведите перпендикуляр $AH$ с $H\in l$. Длина этого перпендикуляра равна расстоянию между точкой $A$ и прямой $l$.
Поскольку угол состоит только из двух лучей, а каждый луч — это отрезок прямой, легко определить расстояние между точкой и сторонами угла. Существует только два перпендикуляра:
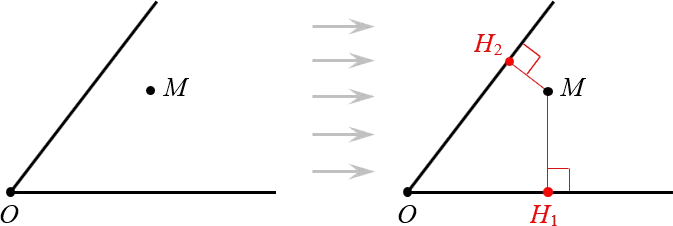
Вот и все! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому мы можем доказать основное свойство.
Как и было обещано, мы разделим доказательство на две части:
Расстояния от точки на биссектрисе до сторон угла одинаковы
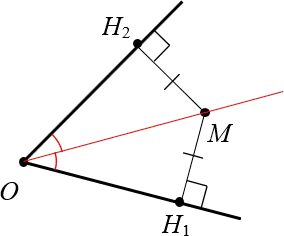
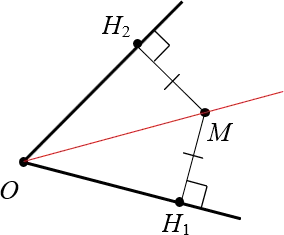
Рассмотрим любой угол с вершиной $O$ и биссектрисой угла $OM$:
Докажите, что одна и та же точка $M$ имеет одинаковое расстояние до сторон угла.
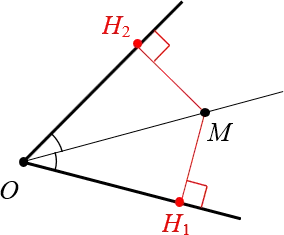
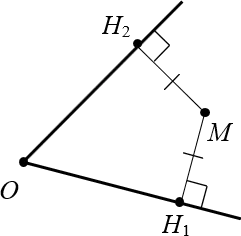
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M_>$ и $M_>$:
Получили два прямоугольных треугольника: $\vartriangle OM_>$ и $\vartriangle OM_>$. Они имеют общую гипотенузу $OM$ и равные углы:
- $\angle MO_>=\angle MO_>$ по условию (поскольку $OM$ — биссектриса);
- $\angle M_>O=\angle M_>O=90<>^\circ $ по построению;
- $\angle OM_>=\angle OM_>=90<>^\circ -\angle MO_>$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M_>=M_>$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Вы должны это доказать).
Биссектриса — это.
Биссектриса угла — это луч, который начинается из вершины треугольника и делит его ровно пополам.
Кроме того, биссектриса угла — это длина отрезка (что это такое?), который начинается в вершине треугольника и заканчивается на противоположной стороне вершины.
Существует также понятие «биссектриса угла», которая является радиусом и делит угол (любой угол, не обязательно треугольник) пополам таким же образом:
Термин bisectrix происходит из латинского языка. И название очень характерное. Оно состоит из двух слов — «bi» означает «двойной, пара», а «sectio» можно буквально перевести как «разрезать, разделять».
Получается, что слово BISSECTRISA означает «разрезать пополам», что и отражено в только что приведенном определении термина.
А теперь проект по закреплению материала. Посмотрите на эти рисунки и скажите, на каком из них изображена дихотомия. Подумайте об этом? Правильно, второй.
На первом рисунке луч, выходящий из угла AOB, явно не делит его пополам. Во втором случае эта связь углов более очевидна, и поэтому можно предположить, что радиус OD — БИССЕКТРИСА. Хотя, конечно, трудно утверждать это на сто процентов.
Для более точного определения используются специальные инструменты. Например, транспортир. Это инструмент в виде полусферы, изготовленный из металла или пластика. Это выглядит следующим образом:

Однако существуют и такие варианты:
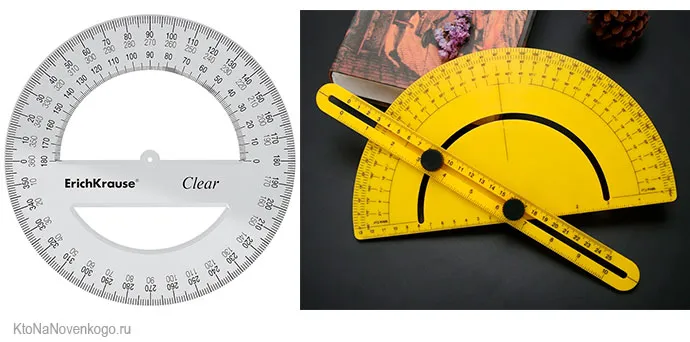
Я уверен, что в школе у каждого был такой. И он очень прост в использовании. Просто совместите основание транспортира (прямоугольной линейки) точно с основанием треугольника, а затем отметьте на полусфере значение, соответствующее величине угла.
И точно такая же система может быть применена в обратном направлении: С помощью транспортира начертите угол нужного размера. Обычно он составляет от 0 до 180 градусов. Но на втором рисунке у нас есть транспортир, который помогает нам чертить градусы от 0 до 360.
Количество биссектрис в треугольнике
Но вернемся к нашей главной теме. И давайте ответим на вопрос: сколько БИССЕКТРОВ в треугольнике?
Ответ в целом логичен и уже заложен в названии нашей геометрической фигуры. У треугольника три угла. Следовательно, существует также три биссектрисы угла — по одной для каждой вершины.
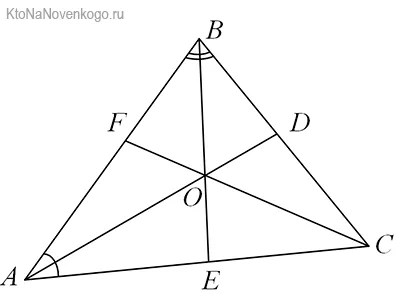
Давайте снова посмотрим на наши рисунки. Здесь мы видим, что треугольник ABC (именно так геометрия определяет этот треугольник — по названию его вершин) имеет три биссектрисы угла. Это сегменты AD, BE и CF.
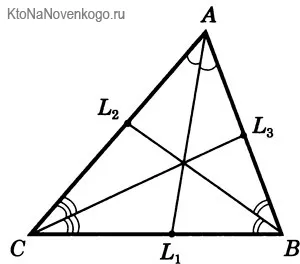
На чертежах БИССЕКТРИСЫ обозначены следующим образом. Видите ли вы одиночные кривые линии между отрезками AC/AL1 и AB/AL1? Так обозначаются углы. И тот факт, что оба обозначены одинаковыми черточками, показывает, что углы одинаковые. Таким образом, сегмент AL1 является БИСЕКТРИЧЕСКИМ.
То же самое относится к углам между AB/DL2 и BC/BL2. Они отмечены одинаковыми двойными тире. Таким образом, отрезок BL2 является бисектрисой. А углы AC/CL3 и BC/CL3 обозначены тройными черточками. Они показывают
Пересечение биссектрис треугольника
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух смежных сторон ().
3. точки биссектрисы угла треугольника равноудалены от сторон этого угла.
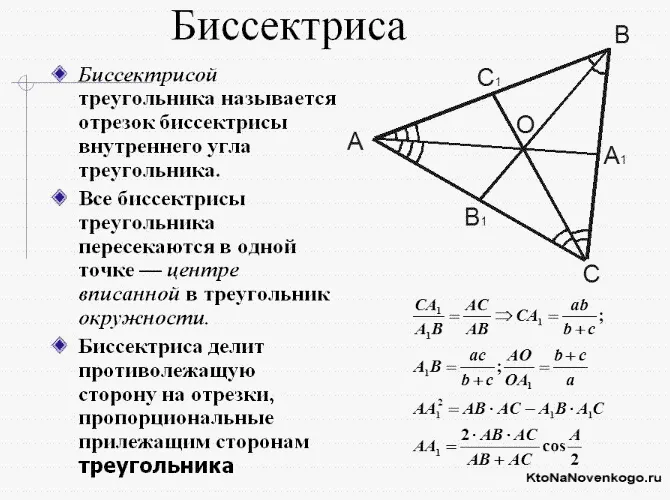
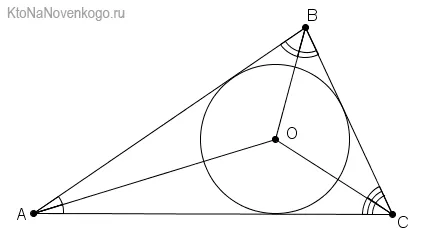
4. Биссектрисы внутренних углов треугольника пересекаются в точке, являющейся центром окружности, вписанной в треугольник.
(Доказательство формулы можно найти здесь), где длины биссектрис, проведенных на стороне, являются сторонами треугольника относительно вершин, или длинами отрезков, на которые биссектриса делит сторону треугольника,
Приглашаю вас посмотреть видео, в котором показано применение всех вышеперечисленных свойств биссектрисы угла.
Задачи, рассмотренные в видео: 1. В треугольнике ABC со сторонами AB = 2 см, BC = 3 см, AC = 3 см проведена биссектриса BM. Найдите длины отрезков AM и MC. 2. Найдите биссектрису внутреннего угла при вершине A и биссектрису внешнего угла при вершине C треугольника ABG, который пересекается в точке M. Найдите угол BMG, если угол B равен 40 градусов, а угол C равен 80 градусов 3. Найдите радиус окружности, вписанной в треугольник, стороны квадратных клеток которого равны 1
Вас также может заинтересовать этот короткий видеоурок, в котором применяется одно из свойств биссектрисы угла
Свойства биссектрисы
Чтобы не пропустить страницу, вы можете сохранить ее для себя:
Некоторые формулы, связанные с биссектрисой треугольника