c) — в этих случаях часть функции, лежащая выше оси Ох, остается неизменной, и эта же часть зеркально отражается вниз симметрично оси демпфирования (Ох). Часть линии, лежащая ниже оси Ох, «исчезает».
Все, что нужно знать о линейной функции. Самые простые методы построения её графика
Что такое линейная функция, какие типы линейных функций существуют, как построить график линейной функции и какие варианты возможны? Обо всем этом и многом другом вы узнаете из этой статьи. Кроме того, мы разберем задачи, связанные с графическим представлением линейной функции и определением коэффициентов ее параметров.
- 1 Что такое линейная функция
- 2 График линейной функции. Самый быстрый способ построить прямую
- 3 Расположение прямой в зависимости от коэффициентов
- 4 Точки пересечения с осями координат
- 5 Условия пересечения, перпендикулярности и параллельности двух прямых
- 6 Задачи, связанные с линейной функцией, и как их решать
Что такое линейная функция
Линейная функция — это функция вида
где — определенные числа, — переменная, — аргумент функции, зависящий от переменной.
Линейная функция также может быть определена следующим образом:
— обычно называется обратной функцией, здесь выражается через (- также частичные числа).
Мы также можем использовать следующее обозначение линейной функции:
Вот некоторые цифры.
Обратите внимание, что переменные и в каждой из приведенных форм являются первой степенью.
Примеры линейных функций:
Второй и третий способы определения линейной функции встречаются редко (обычно при решении систем линейных уравнений). Первая форма используется для построения диаграммы.
График линейной функции. Самый быстрый способ построить прямую
Первая и вторая формы используются для построения графика линейной функции. (Линейная функция называется так, потому что ее график — прямая линия).
Чтобы провести прямую линию, нужно знать только 2 точки. Поскольку аргумент зависит от переменной, нужно взять любые два значения и подставить их в функцию, тогда мы получим два значения. Построим эти две точки с координатами и в координатной плоскости и проведем через них прямую линию.
Рассмотрим на конкретном примере, как построить график линейной функции.
Таким образом, у нас есть функция .
Возьмем 2 значения, скажем 0 и 1, и поместим их в функцию:
Возьмем две точки и отметим их на координатной плоскости:
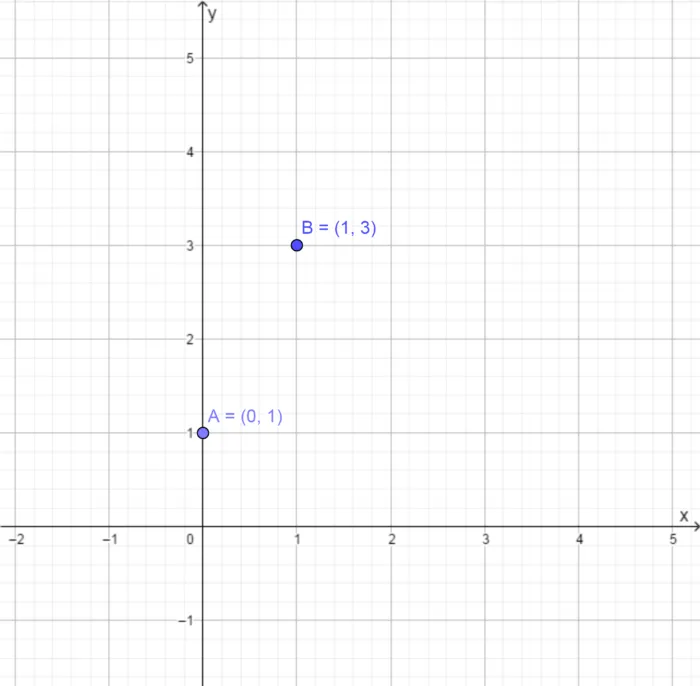
Теперь проведем прямую линию, проходящую по линейке через обе точки:
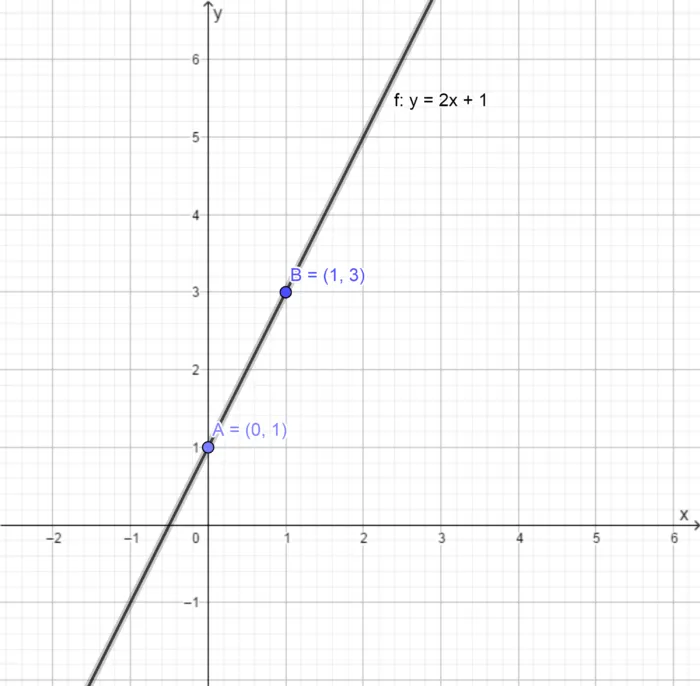
Этот метод построения прямой линии приведен в учебном плане. Однако существует очень простой и быстрый способ провести границу. Чтобы использовать этот метод, мы напишем нашу функцию следующим образом:
С помощью этой нотации мы не изменили и не «сломали» функцию, потому что .
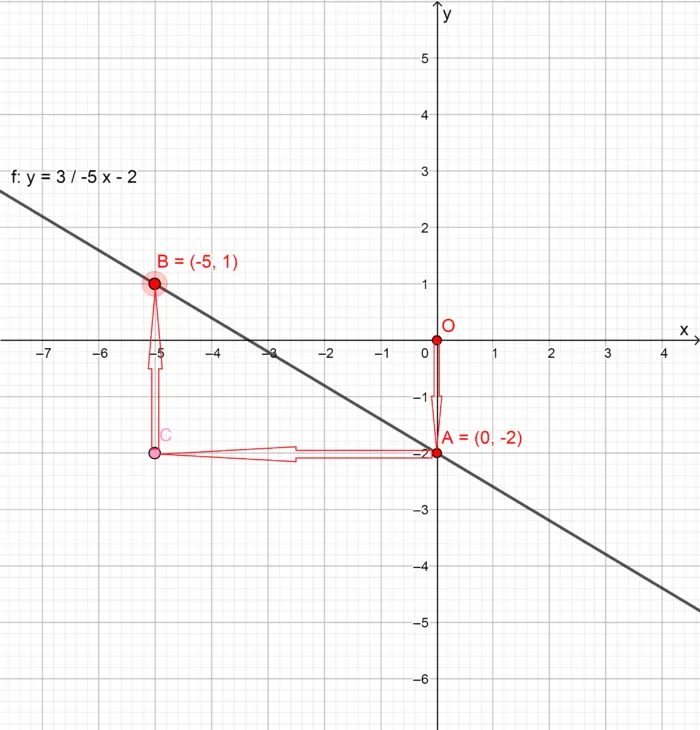
1. значение свободных терминов. От пересечения O(0;0) с осью O в координатной плоскости отсчитываем 1 (от ) и ставим в этой точке первую точку A(0;1) (на рисунке заштрихована красным).
2. значение намеренно было представлено в виде дроби, чтобы при использовании значений первого знаменателя, равных
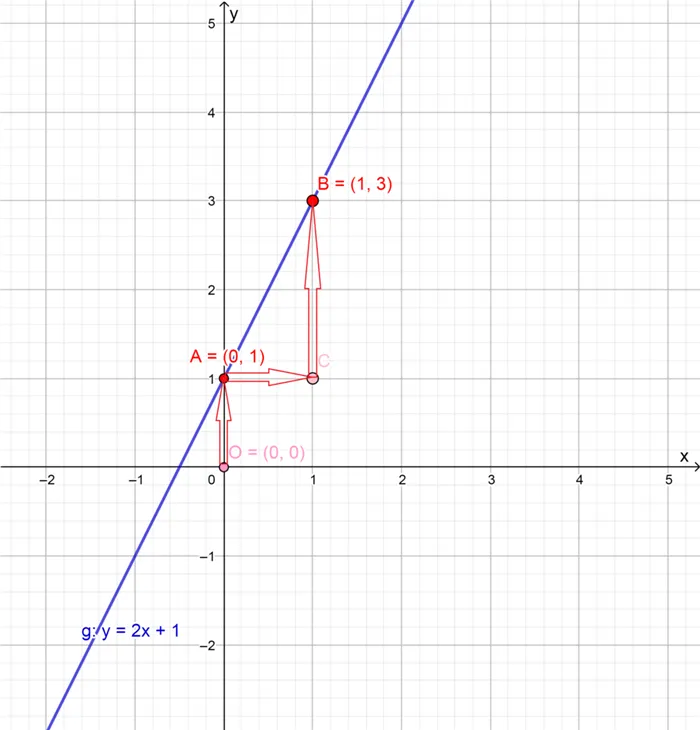
Теперь мы знаем, как двигаться: вниз на 2 (d a-2) — у нас первая точка A, влево на 5 (d a-5) — промежуточная точка C, вверх на 3 (da +3) — вторая точка B, проводим прямую линию через точки A и B:
Чтобы определить, как на диаграмму влияют
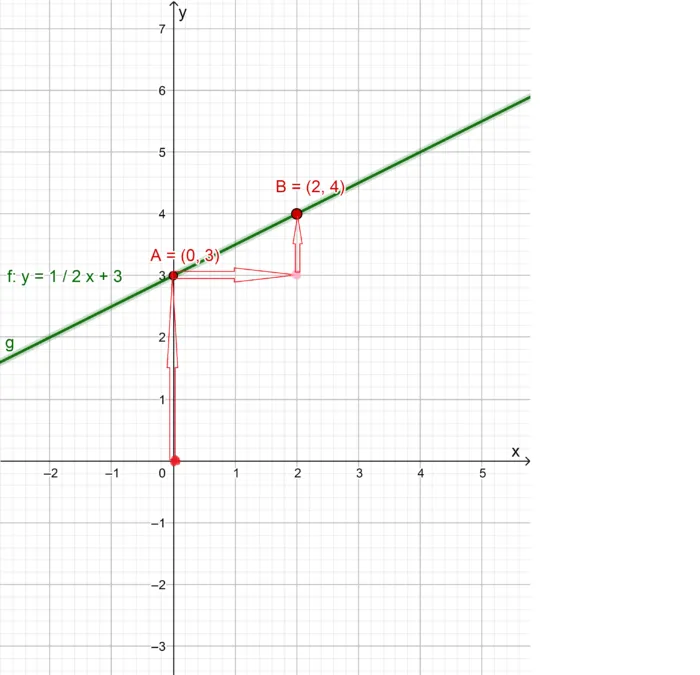
Коэффициент
\(k\) несколько функций с разными \(k\): \(\frac\),\(-\frac\),\(2\),\(-2\) и \(0\). В этом случае \(b\) делается равным (равным нулю) во всех функциях, чтобы устранить его влияние. Другими словами: Мы рисуем графики функций.
Обратите внимание, что функция возрастает для \(k=2\) и \(\frac\), в то время как она убывает для \(k=-2\) и \(-\frac\). На самом деле:
Как меняется график при разных \(k\)?
0\) функция возрастающая и для каждого \(k.Мы также видим, что чем большекоэффициенты
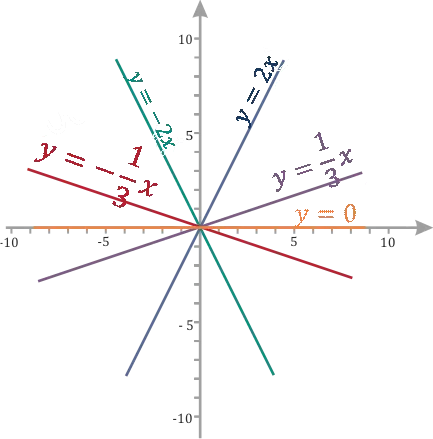
\(k\), тем круче график.
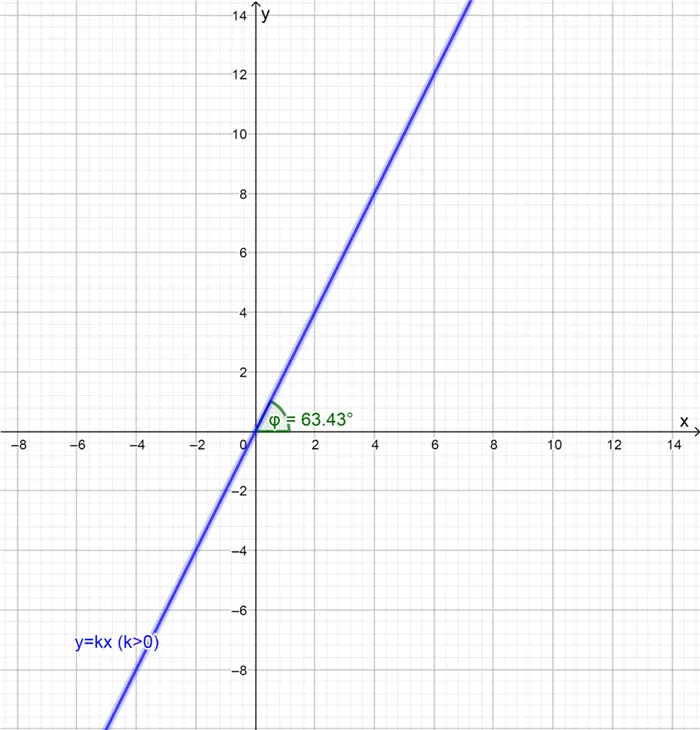
При любом \(k>Чтобы найти значение \(k\) по модулю (т.е. не обращая внимания на знак), нужно разделить вертикальную сторону треугольника на горизонтальную. Вы можете применить эмпирическое правило: «Стоять лучше, чем лежать». В этих случаях \(|k|=\frac\). Поэтому в первой диаграмме \(k=2\), а во второй \(k=-\frac\).
Чтобы увидеть, как \(b\) влияет на график, мы построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\).0\)), или проходит через \(|b|\), если (\(bПостройте график функции y= -3x+4. Создадим таблицу для двух значений, например, 0 и 2.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

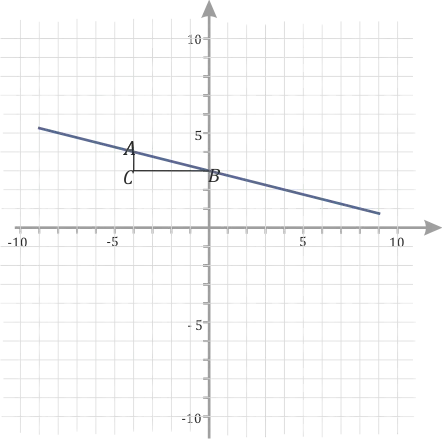
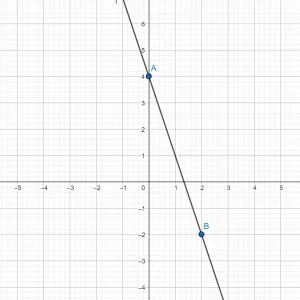
Из формулы видно, что угловой коэффициент отрицательный, поэтому линия уменьшается. Постройте нисходящую прямую в системе координат через две точки A(0;4) и B(2;-2).
Как меняется график при разных значениях \(b\)?
Постройте график функции y=4. Видите, что в данном случае x=0, поэтому прямая, проходящая через точку с координатами (0;4), будет параллельна оси x. Это показано на следующем графике:
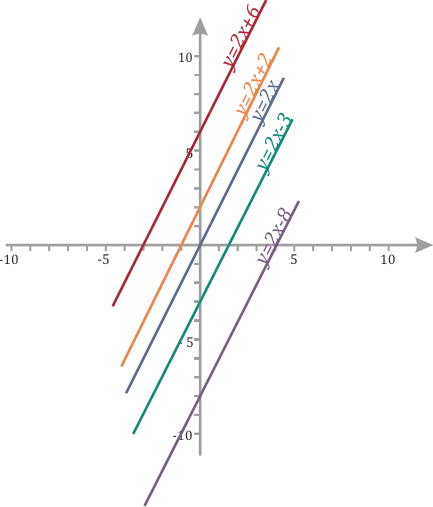
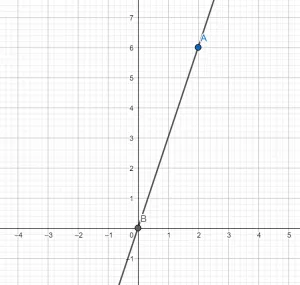
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>Постройте график функции y=3x. Эта функция является частным случаем, когда линия проходит через начало координат. Поэтому в данном случае мы можем взять только одно значение x, например, 2, чтобы y было равно 6. Итак, у нас есть две точки (2;6) и (0;0), которые мы строим в системе координат и через которые проводим прямую, которая поднимается, так как угловой коэффициент равен 3, то есть положительный.<0\)).
Пример №2.
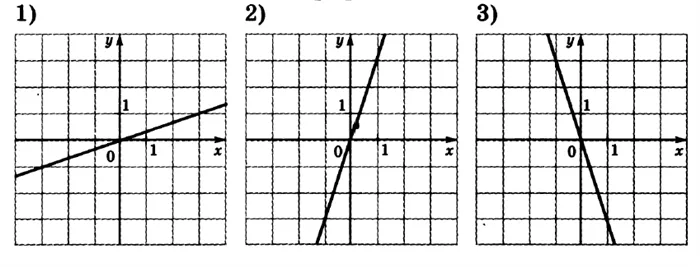
Графики функций вида y=kx+b показаны на рисунках. Установите соответствие между графиками функций и знаками коэффициентов k и b.
0. Это соответствует оставшимся графикам A и B, так как оба они наклонены в положительном направлении оси O под острым углом (
Пример №3
0, что соответствует графику A, пересекающему ось O выше начала координат. Это делает необходимым
Термин «линейная функция» или, более точно, «линейная однородная функция» часто применяется к линейному представлению векторного пространства в данной области, т.е. к этому представлению и к любому
в этом случае вместо термина «линейная функция» используются также термины «линейная функция» и «линейная форма», под которыми также понимается линейная однородная функция определенного класса.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>Основная статья: Булева линейная функция, полином Жегалкина, пост-критерий.
В 1-й паре коэффициентов bБ–1. В паре коэффициентов №2 b>что для любого
Для функций, которые являются нелинейными (т.е. совершенно произвольными), термин нелинейные функции используется, когда мы хотим подчеркнуть определенные свойства. Обычно это происходит, когда функциональная зависимость сначала аппроксимируется линейной зависимостью, а затем рассматривается более общий случай, часто начиная с наименьших мощностей, например, с учетом квадратичных поправок.
То же самое относится к использованию слова нелинейный по отношению к другим объектам, которые не обладают свойством линейности, например, нелинейные дифференциальные уравнения.
В некоторых случаях этот термин может применяться и к зависимостям, то есть нелинейным линейным функциям, поскольку они не обладают свойством линейности, как в случае с. Нелинейная зависимость — это, например
- если k<0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k>0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b<0, то прямая пересекает ось y ниже 0 в точке y = b, если b>0, то выше ноля в точке y = b
- если k>
<0, и график идет сверху вниз.
Линейная функция
Абстрактная алгебра
Алгебра логики
Булева функция, где » width=»» height=»» />








