Выражение C ИЛИ D верно для 8000 сайтов и 6000000 сайтов в целом. Поэтому выражение C OR D не верно для 5992000 сайтов. Другими словами, выражение NOT (C OR D) верно для 5992000 сайтов.
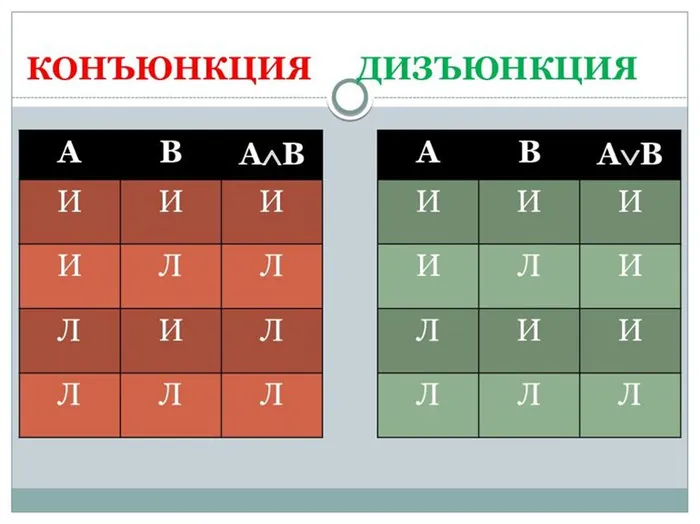
Конъюнкция
Конъюнкция (от лат. conjunctio — соединение, связь) — это логическая операция, которая максимально приближена к использованию связки «и». Синонимы: логическое И, логическое умножение, иногда просто И.
Конъюнкция может быть бинарной операцией с двумя операторами, тринарной операцией с тремя операторами или n-арной операцией с n операторами. Наиболее распространенные варианты: в инфиксной нотации:
,
По аналогии с умножением в алгебре, символ логического умножения может быть опущен: в префиксной нотации:
Содержание
- 1 Булева алгебра
- 2 Многозначная логика
- 3 Классическая логика
- 4 Схемотехника
- 5 Программирование
- 6 Связь с естественным языком
- 7 Примечания
- 8 См. также
Определение. Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция ( логи́ческое «И», логи́ческое умноже́ние или просто «И» ). Правило: результат равен наименьшему операнду. Описание. В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества. Результат также принадлежит множеству. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений или false» width=»» height=»» />В арифметической системе счисления старшинство, конечно, равно. Правило: результат равен ; во всех остальных случаях результат равен.
Таблицы истинности: для бинарной конъюнкции
Для троичной конъюнкции
| X | Y | Z | X Y Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабому дизъюнкту 1.
Многозначная логика
Операция, называемая соединением в двоичной логике, называется минимумом в многозначной логике: и
Заметим, что название операции Minimum имеет смысл в логиках любого знака, включая двоичную логику, а названия Coupling, Logical «AND», Logical Multiplication и Simple «AND» имеют смысл только в двоичных логиках и теряют смысл при переходе к многозначным логикам.
Конъюнкция
Рассмотрим следующие утверждения: C = «Небо голубое», D = «Трава зеленая». Очевидно, что составное высказывание «Небо голубое, а трава зеленая» истинно только в том случае, если оба исходных высказывания истинны одновременно.
Сопряжение — это логический процесс, который объединяет два высказывания в другое высказывание, которое истинно только в том случае, если оба исходных высказывания истинны.
Для записи конъюнкции мы используем следующие знаки: И, ˄, -, &. Например: C AND D, C ˄ D, C — D, C&D.
Связь представлена в виде таблицы, называемой таблицей истинности:
| C | D | C ˄ D |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблица истинности содержит все возможные значения начальных утверждений, а соответствующие двоичные числа обычно располагаются в порядке возрастания: 00, 01, 10 и 11. Последний столбец содержит результат логической процедуры для указанных операторов.
Дизъюнкция
Обратите внимание на следующие утверждения: C = «Облака плывут по небу», D = «Днем облака белые». Новое высказывание «Облака плывут по небу или облака днем белые» не является истинным только в том случае, если оба исходных высказывания одновременно ложны.
Дисъюнкция — это логический процесс, который соединяет два высказывания с другим высказыванием, которое считается ложным только в том случае, если оба исходных высказывания ложны.
Для описания дизъюнкции используются следующие обозначения: ИЛИ, ˅, | и +. Предположим, что C OR D, C ˅ D, C | D, C + D. Используются следующие выражения: C ИЛИ D, C ˅ D, C | D, C + D.
Дисъюнкция обозначается таблицей истинности:
| C | D | C ˅ D |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Инверсия
Инверсия составляет l
Поэтому для образования отрицания простое высказывание должно содержать фразу «не верно, что…», в противном случае отрицание присоединяется к предикату, т.е. молекула «не» присоединяется к рассматриваемому глаголу.
Каждый составной оператор записывается в виде логического выражения, выражения с логическими переменными, нотации логического процесса и скобок. Логические процессы в логическом выражении выполняются один за другим: Инверсия, конъюнкция и дизъюнкция. Процедуры можно отменить с помощью круглых скобок.
| C | Если в формуле указаны круглые скобки, порядок их выполнения точно такой же, как написано выше. |
| 0 | 1 |
| 1 | 0 |
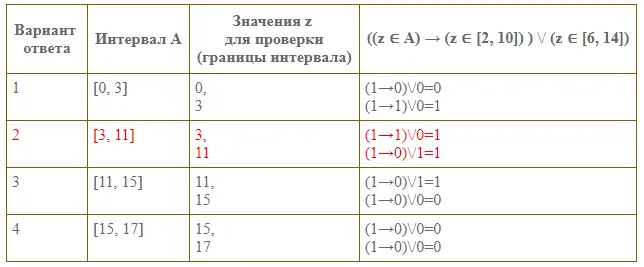
Даны два отрезка B = 2,10, C = 6,14. Выберите из данных ответов такой отрезок A, для которого формула \((z \в A) \Longrightarrow (z \в B)) \vee (z \в C)\) верно для каждого значения z. Варианты ответов:
Решение: подставим \( ((z \в A) \Longrightarrow (z \в B)) в уравнение. \вее (z \в C) \) = 1, и сформировать таблицу истинности:
Полученная формула \( ((z \in A) \Longrightarrow (z \in 2,10)) \вее (z \в 6,14)=1 \). По условию, \( z \ в A \)=1.
Порядок выполнения операций
Таблица истинности для всех сегментов:
- Первой выполняется инверсия переменных.
- Вторым выполняется конъюнкция (булево умножение);
- Третьим номером идет дизъюнкция (сложение);
- Затем выполняется импликация ;
- Самым низким приоритетом выполнения обладает эквивалентность .
Ответ.
Пример
Логическая связка — это бинарная операция над высказываниями, результатом которой является истинное высказывание только в том случае, если истинны исходные высказывания.
Другими видами конъюнкции являются логическое умножение, логическое И или простое И.
Конъюнкция изучается в информатике в части алгебры логической алгебры.
В естественных языках конъюнкция заменяется конъюнкцией AND.
0 и x=10 & a
Конъюнкция
Для обозначения соединений используется символ ∧ или &.
Поскольку на клавиатуре нет символа соединения (∧), удобно вводить его с помощью комбинации вертикальной и обратной косой черты /\.
Истинность соединения определяется таблицей истинности.
A /\ B
В языках программирования для конъюнкции используют обозначение ‘ and ‘ или знак амперсанд ‘ & ‘ (либо ‘ && ‘) (например, x>Представьте, что A и B — это высказывания, где 0 — открытый выключатель, а 1 — закрытый. Лампочка представляет собой соединение. Если лампа не горит, то это 0, а если горит — 1. Тогда очевидно, что лампочка горит только тогда, когда оба выключателя замкнуты, что полностью соответствует таблице истинности для данного соединения.
Просмотры страниц.
Как набрать знак конъюнкции на клавиатуре
Таблица истинности для конъюнкции
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Электрический аналог конъюнкции