Примечания: Если вы нашли в своей задаче хотя бы одну точку параллелограмма, то вы точно параллелограмм и можете использовать все свойства параллелограмма.
Определение параллелограмма
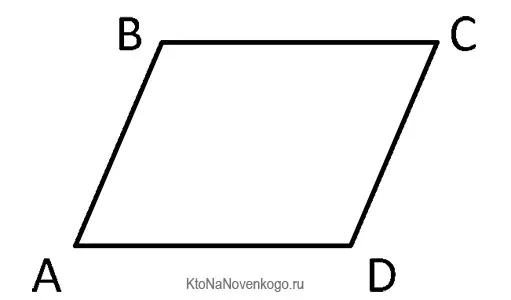
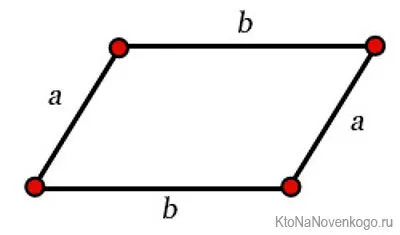
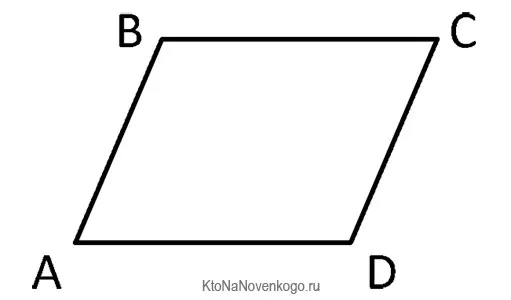
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и попарно равны. Вот как выглядит параллелограмм:
Особые случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — это отрезки, соединяющие противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, соединяющий вершину с точкой на одной из двух противоположных сторон и делящий угол пополам у вершины.
Свойства биссектрисы угла параллелограмма:
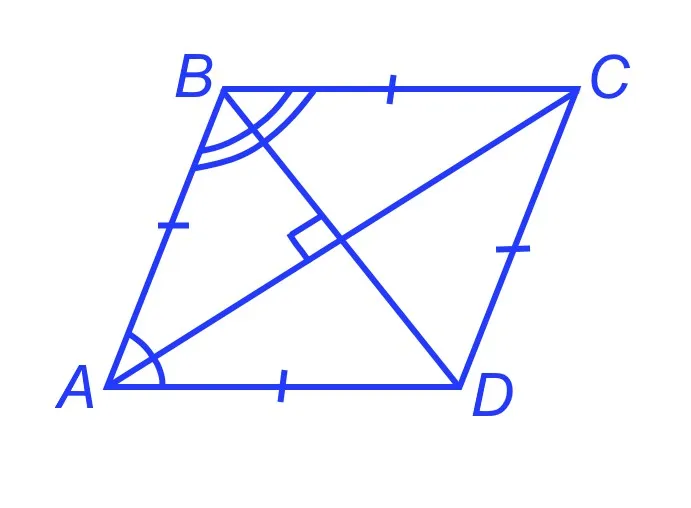
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
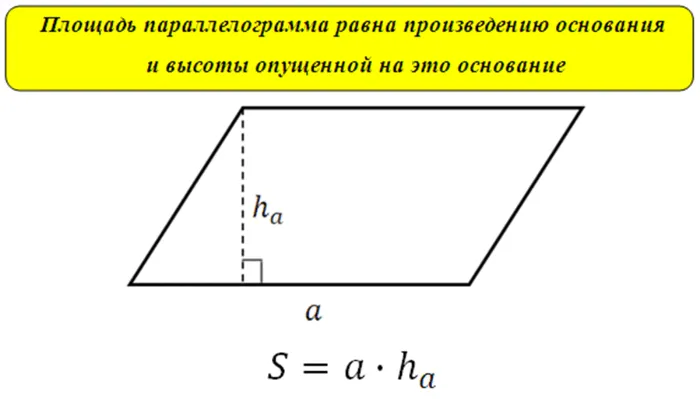
Как определить площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.
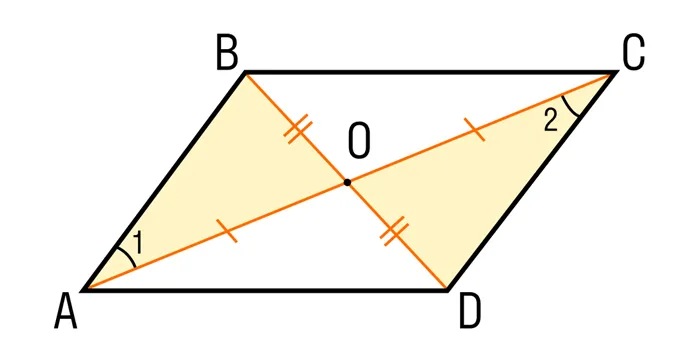
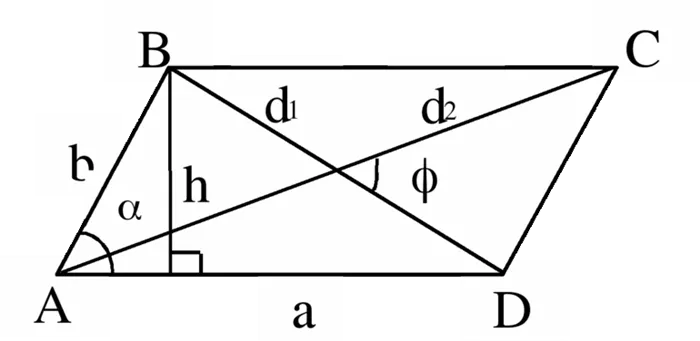
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
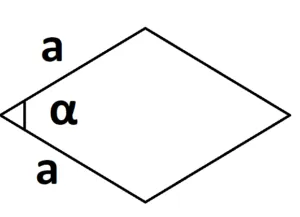
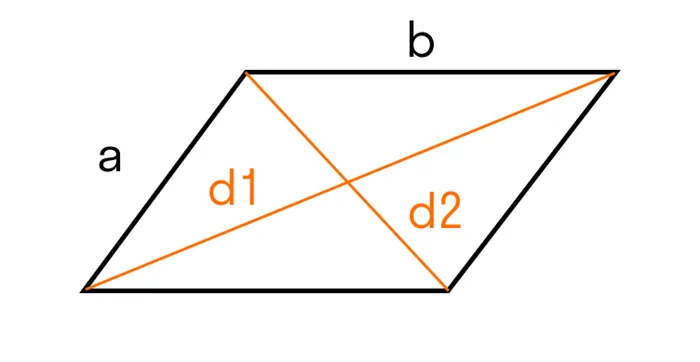
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.

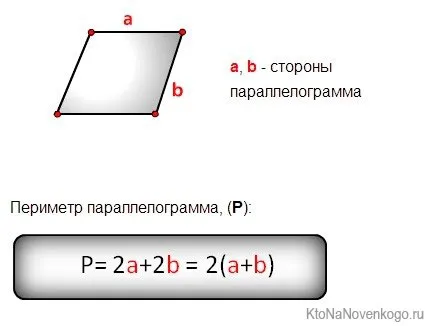
Периметр параллелограмма равен сумме его длины и ширины, умноженной на два.
P = 2 × (a + b), где a — ширина, а b — высота.
У нас есть отличные дополнительные занятия по математике для учеников с 1 по 11 класс!
Узнайте, какие темы вызывают у вас трудности, и решите их без формул и скучных лекций.

Свойства параллелограмма
Геометрическая фигура — это любой набор точек. Каждая фигура имеет свои свойства, которые отличают их друг от друга и помогают решать задачи по геометрии в 8 классе.
Давайте рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем, что дает сумма углов параллелограмма, и познакомимся с другими особенностями этой фигуры. Вот он:
- Противоположные стороны параллелограмма равны. ABCD — параллелограмм, значит, AB = DC, BC = AD.
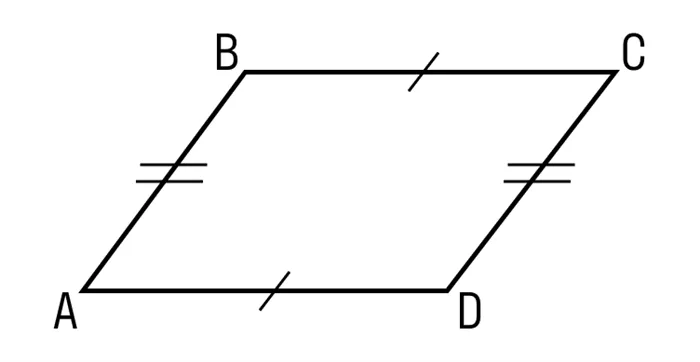
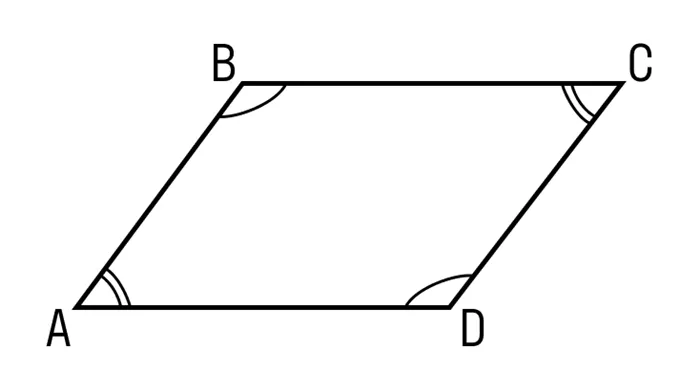
- Противоположные углы параллелограмма равны. ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
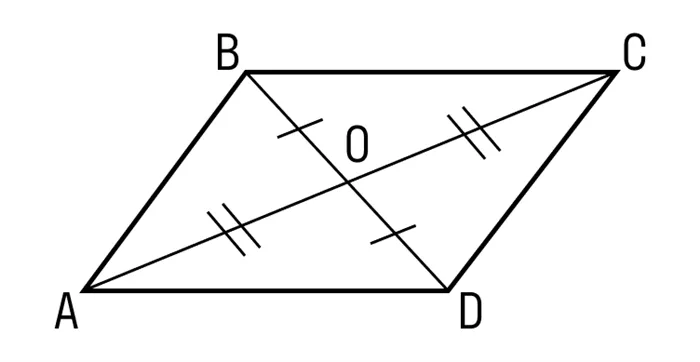
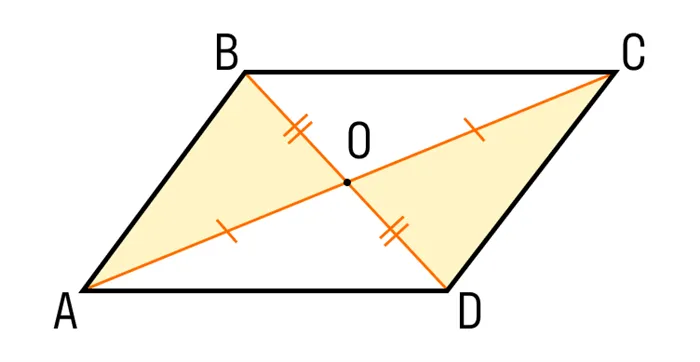
- Диагонали параллелограмма точкой пересечения делятся пополам. ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
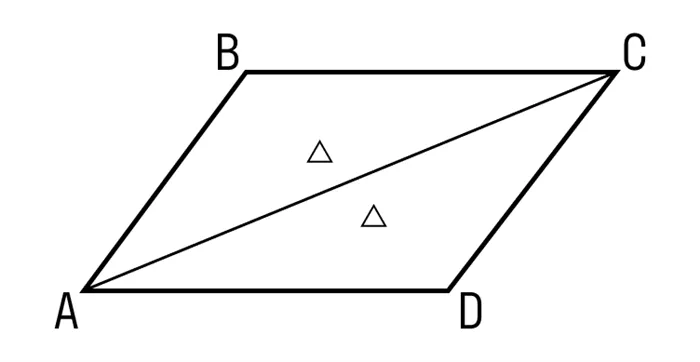
- Диагональ делит параллелограмм на два равных треугольника. ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
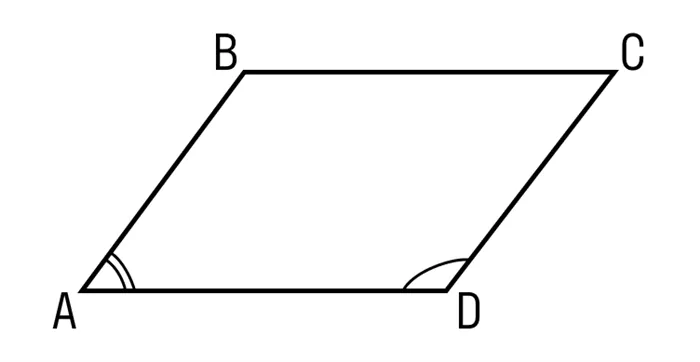
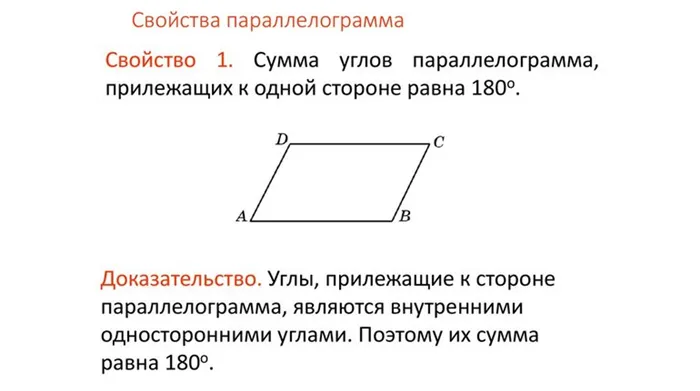
- Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам. ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
- В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
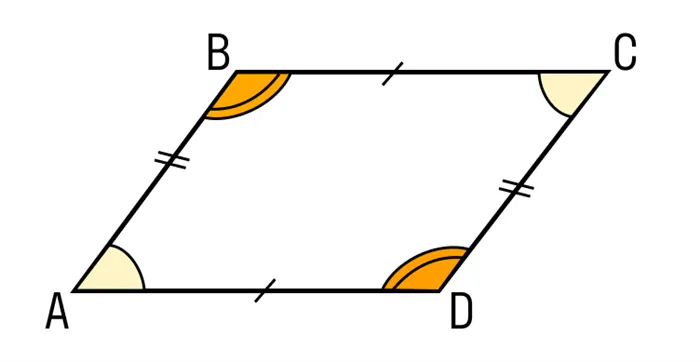
Теперь докажем теорему, основанную на первых двух свойствах.
Теорема 1: В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем об их пересечении, это то, что оно лежит внутри четырехугольника.
Если провести две диагонали на прямоугольнике, то они разделятся на две половины точкой пересечения. Давайте посмотрим, так ли это:
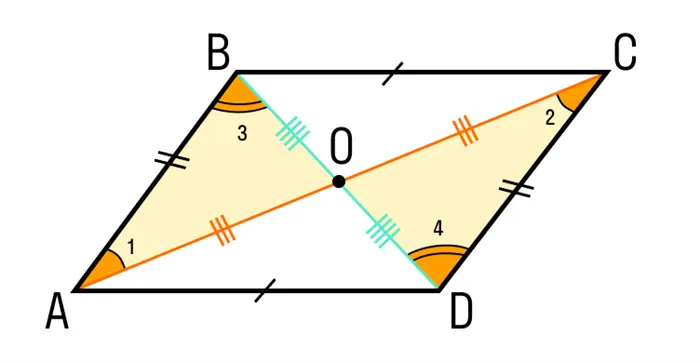
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наша гипотеза верна.
Признаки параллелограмма
Символы параллелограмма помогают нам распознать эту фигуру среди других четырехугольников. Отметим три существенных момента.
Первая точка параллелограмма. Если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник является параллелограммом.
Докажем 1-й признак параллелограмма:
Шаг 1. Возьмем четырехугольник ABCD:
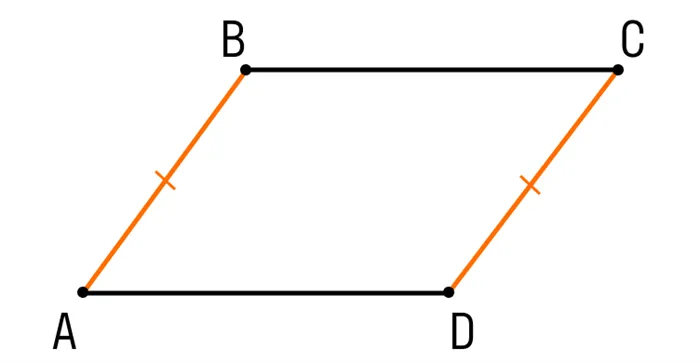
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Теперь мы видим пару параллельных сторон. Мы должны доказать, что вторая пара сторон также параллельна.
Шаг 2 Проведите диагональ. Возьмите два треугольника ABC и CDA, которые равны по первой точке равенства, то есть две стороны и угол между ними:
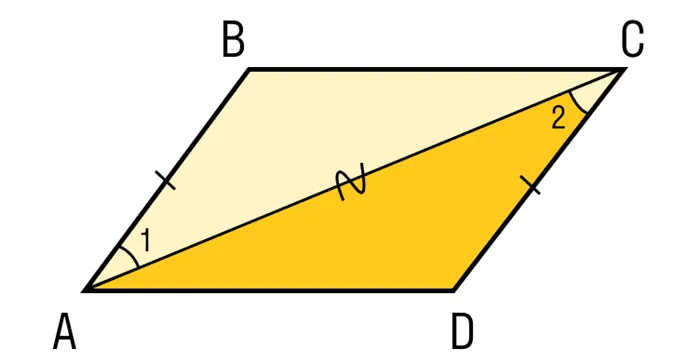
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.
Шаг 3. Это также следует из равенства треугольников:
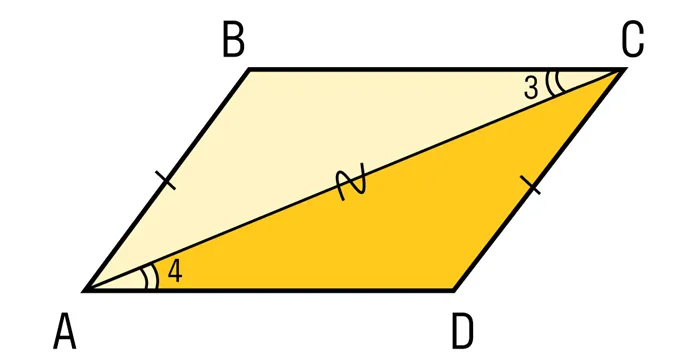
Эти углы также являются внутренними углами пересечения прямых CB и AD. А это как раз и есть признак параллельности линий.
Шаг 1. Если диагонали четырехугольника ABCD пересекаются точкой O, то треугольник AOB равен треугольнику COD с двумя сторонами и углом между ними:
Параллелограмм — это геометрическая фигура, которая является разновидностью четырехугольника. Его противоположные стороны лежат на параллельных прямых и поэтому параллельны друг другу.
Эта форма выглядит следующим образом:
Шаг 1. Возьмем четырехугольник ABCD:
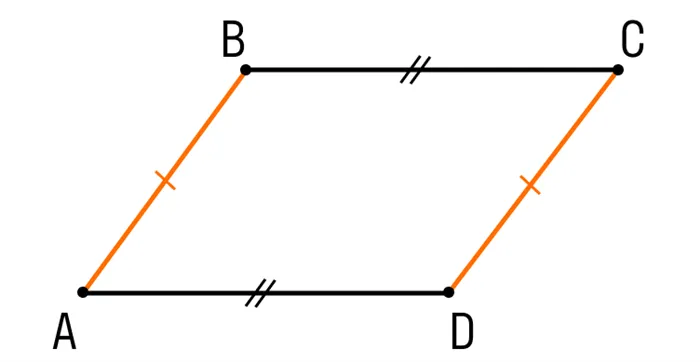
- AB = CD
- BC = AD
Интересно, что наиболее знакомые нам фигуры — квадрат, прямоугольник и ромб — также являются параллелограммами.
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.
Мы даже можем дать такие определения:
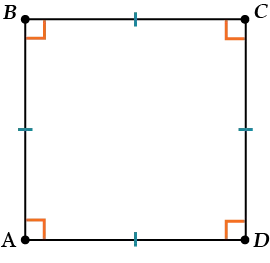
Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- ∠ DCA = ∠BAC А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАФ пришло из Древней Греции. И легко предположить, что это как-то связано с самым известным математиком в истории, Евклидом.
Это действительно так. Слово ПАРАЛЛЕЛОГРАММА впервые встречается в работе Евклида «Элементы». Оно состоит из двух греческих слов — parallelos, что, конечно же, означает «параллельный», и gramme, «линия».
Поэтому PARALLELOGRAM можно перевести как «параллельные линии». Именно этот принцип лежит в основе определения геометрической фигуры.
Еще один любопытный факт заключается в том, что Евклид разделил все четырехугольники на две основные категории. Первый — это параллелограмм, у которого противоположные стороны параллельны. И трапеции (что это такое?), у которых только одна пара сторон параллельна.
Определение параллелограмма
Как узнать, является ли он ПАРАЛЛЕЛЬНЫМ? Этой геометрической фигуре присущи определенные особенности.
В качестве примера снова возьмем нашу форму:
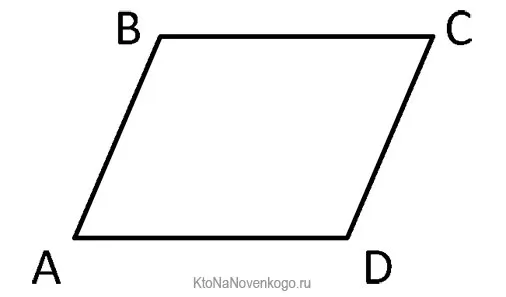
Чтобы этот четырехугольник ABCD считался параллелограммом, должно выполняться одно из следующих условий:
Две противоположные стороны попарно параллельны.
Это самые простые точки параллелограмма. Есть еще несколько знаков, значение которых объясняется в этом видео:
-
Более того, чтобы проверить подлинность фигуры, достаточно доказать только одну из них.
Происхождение термина «параллелограмм»
Это правило работает и в обратную сторону: если хотя бы один из признаков параллелограмма истинен, то все остальные признаки также автоматически истинны и не требуют отдельного доказательства.
Если хотя бы один признак не доказан, фигура также не может считаться параллелограммом. И все остальные тоже не согласны.
Думаю, для вас не новость, что….

Прямоугольник — это четырехугольник, все углы которого прямые.
Свойства и признаки параллелограмма
Первый вопрос: является ли прямоугольник параллелограммом?
Потому что у него \( \Displaystyle \angle A=\angle C\links( =90
(и \( \Displaystyle \angle B=\angle D\links( =90
-
^\\\circ
ight)\) — помните, наш знак 3?
Отсюда следует, что n
Точка с параллелограммом вполне очевидна — выполнен только знак 3 (\( \displaystyle \угольник A=\угольник C\) \( \displaystyle \угольник B=\угольник D\)).
А пункт о диагоналях очень важен. Итак, мы хотим доказать, что диагонали прямоугольника равны.
Прямоугольник – определение и свойства
Мы постоянно работаем над улучшением этого учебника, и вы можете нам помочь. Получите доступ к учебнику Юклавы и пользуйтесь им без ограничений (100+ статей по всем темам ЕГЭ и ОГЭ, 2000+ решенных задач, 20+ вебинаров и учебников).
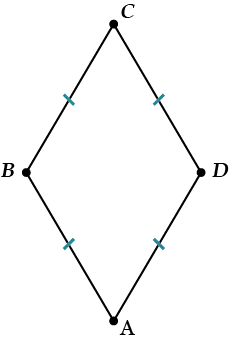
Ромб — это четырехугольник, у которого все стороны одинаковой длины.

И снова вопрос: является ли ромб параллелограммом или нет?
Это определенно параллелограмм m, потому что он имеет \( \displaystyle AB=CD\) и \( \displaystyle BC=AD\) (см. доказательство 2).<>Поскольку ромб является параллелограммом, он также должен обладать всеми свойствами параллелограмма. Это означает, что противоположные углы ромба равны, противоположные стороны параллельны, а диагонали делятся на две половины точкой пересечения.<>Но есть и особые свойства. Мы формулируем.
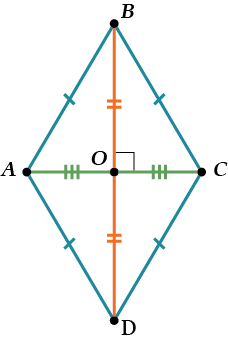
Свойство 1. Диагонали ромба перпендикулярны друг другу.
Почему? Поскольку ромб является параллелограммом, его диагонали делятся посередине.
Итак, \( \displaystyle \Delta BOC=\Delta DOC\) с трех сторон (\( \displaystyle BO=OD\), \( \displaystyle OC\) общие, \( \displaystyle BC=CD\)).

И так, \( \displaystyle BOC=\угольник COD\), но они смежные!
\(\displaystyle \стрелка вправо \угольник BOC=90

^/контур \) и \( \дисплейстайл \угол COD=90
Докажем, что диагонали прямоугольника равны
^/circuit \).
Свойство 2. Диагонали ромба являются биссектрисами его углов.
Открыть ответы…
Почему? Потому что.
Ромб – определение и свойства
Поскольку диагонали делят пересечение пополам, а все стороны ромба равны, весь ромб делится диагоналями на четыре равных треугольника:
\{\Displaystyle \Delta BOC,\text
\Дельта BOA,/Дельта AOD,/текст
\Delta COD.)
\(\displaystyle \угольник 1=\угольник 2;\текст
Свойства ромба
\угол 5=угол 6;\) \(\displaystyle \угол 3=угол 4;\text
\угол 7=угол 8;\)
Другими словами, диагонали \(\displaystyle BD\) и \(\displaystyle AC\) являются биссектрисами углов ромба.
Как и для прямоугольника, эти свойства являются характерными, и каждое из них также является свойством ромба.
Доказательство 1. Если диагонали прямоугольника перпендикулярны друг другу, то он является ромбом.<>\( \displaystyle \left\<>\(\displaystyle ABCD\) — параллелограмм \(\displaystyle \Rightarrow AO=CO;BO=OD\).
Но также дано, что \( \displaystyle AC\bot BD\) \( \displaystyle \Rightarrow\) \( \displaystyle \Delta AOB=\Delta BOC=\Delta COD=\Delta AOD\) состоит из двух зондов.
И так \displaystyle AB=BC=CD=AD\) — вот и все!
Доказательство 2. Если в параллелограмме хотя бы одна из диагоналей делит два угла, через которые она проходит, на две половины, то этот параллелограмм является
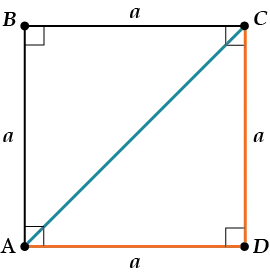
Ну, это совершенно ясно: диагонали прямоугольника \( \displaystyle \Rightarrow \) равны; диагонали ромба \( \displaystyle \Rightarrow \) перпендикулярны, и вообще диагонали параллелограмма \( \displaystyle \Rightarrow \) делят пересечение на две половины.<>Если сторона квадрата равна \( \displaystyle a\), то его диагональ равна \( \displaystyle a\sqrt\).<>Почему? Ну, просто примените теорему Пифагора к \( \displaystyle \Delta ADC\).
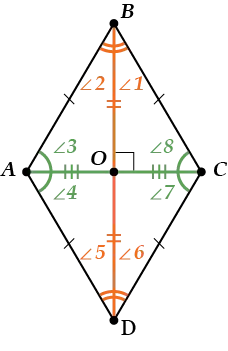
Поэтому \( \displaystyle AC=\sqrt\cdot a\).<>На этом теория параллелограмма заканчивается. Если вы хотите попрактиковаться в решении задач, посмотрите наши вебинары в разделе бонусов.<>Частным случаем параллелограмма является ромб.
Ромб — это параллелограмм, у которого все стороны равны. Свойства ромба такие же, как и у параллелограмма. Однако есть одна особенность: диагонали ромба перпендикулярны и являются биссектрисами углов.
В следующих статьях мы рассмотрим ромб более подробно, а также докажем это свойство ромба для его диагоналей.
Признаки ромба
<\beginAC\bot BD\\ABCD\ – параллелограмм\end \right.\Rightarrow\) \( \displaystyle \Rightarrow \) \( \displaystyle ABCD\) – ромб
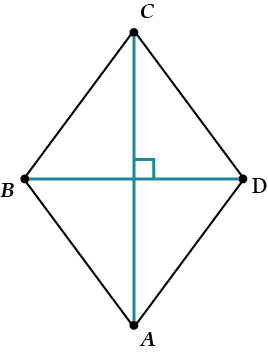
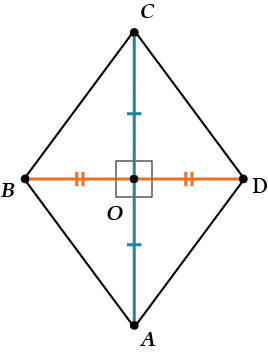
Квадрат – определения и свойства
<>
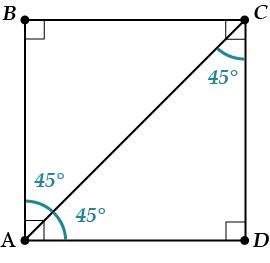
<>\(\displaystyle ABCD\) — параллелограмм \(\displaystyle \Rightarrow AO=CO;BO=OD\).
<>\(\displaystyle ABCD\) — параллелограмм \(\displaystyle \Rightarrow AO=CO;BO=OD\).

Частный случай параллелограмма