Что такое бином Ньютона и почему им всех пугают. Бином ньютона что это?

4) Обозначив каждый член расширения буквой T, с цифрой внизу, указывающей номер позиции этого члена в расширении, т.е. первый член T₁, второй член T₂ и т.д., мы можем написать:

Что такое бином Ньютона и почему им всех пугают

Далее мы поговорим о различных формулах и подходах из математики, которые часто используются в информатике и в известных алгоритмах. Сегодня мы рассмотрим бином Ньютона — многие слышали о нем, но не все знают, что это такое и для чего он используется. Давайте посмотрим на это.

Чтобы понять бином Ньютона, нам нужен треугольник Паскаля.

Что такое треугольник Паскаля

Треугольник Паскаля — это одно из названий треугольной матрицы чисел. Он назван в честь математика Блеза Паскаля, но математики знали об этом треугольнике еще тысячу лет назад.

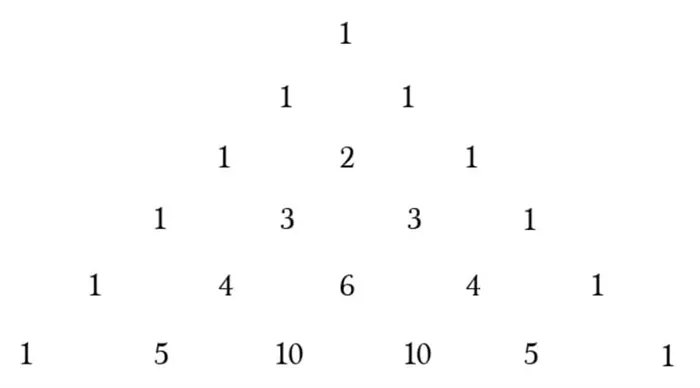
Принцип работы треугольника заключается в том, что мы берем одно число (которое является вершиной треугольника) и получаем все остальные числа в каждом ряду, складывая числа слева и справа над ним. Когда вы нарисуете его, он будет выглядеть следующим образом:

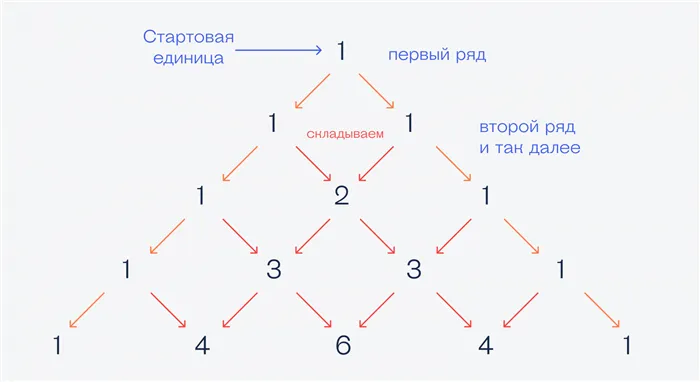
Такой треугольник можно продолжать бесконечно. В математике этот треугольник обладает рядом полезных свойств, но нам он нужен для биномиальных коэффициентов в биномиальной системе Ньютона. Теперь поговорим о биноме.

Что такое бином Ньютона (просто)

Биномиальная формула Ньютона — это формула для вычисления суммы двух чисел, умноженных на степень.

Давайте посмотрим на это:

У нас есть некие числа a и b. Мы не знаем какие, потому что алгебра.
Не зная, что это за числа, мы их складываем.
Эту сумму почему-то очень хочется возвести в какую-то степень — в квадрат, в куб, в четвертую, хоть в девятьсот девяносто девятую — алгебре плевать на ваши чувства.
Нам нужна формула, как это сделать. Вот эта формула и есть бином Ньютона.

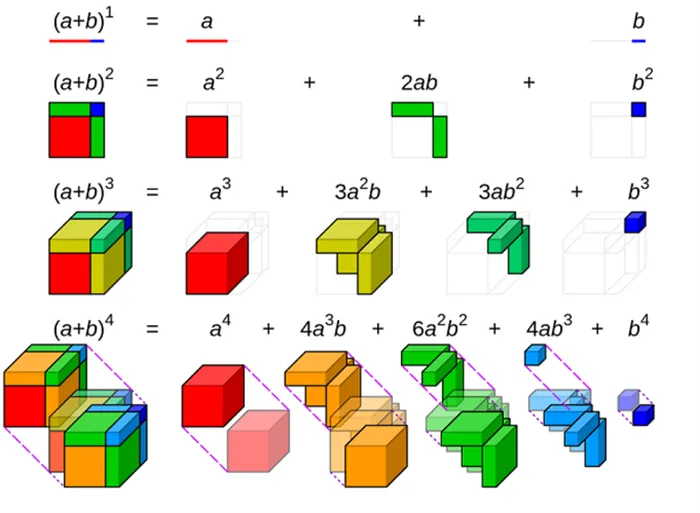
Из школьных уроков мы знаем следующую формулу: (a + b) 2 = a 2 + 2ab + b 2 — это частный случай биномиальной формулы Ньютона для квадрата суммы.

Вы можете вспомнить сумму в кубе: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 — это также бином Ньютона.

Но что если нам нужно взять сумму не в квадрате, не в кубе, а в сорок шестой степени? Какой будет формула? Для этого нам нужна более общая формула, которая описывает все вариации биномиальных чисел для произвольной силы.

Вот эта формула в общем виде:

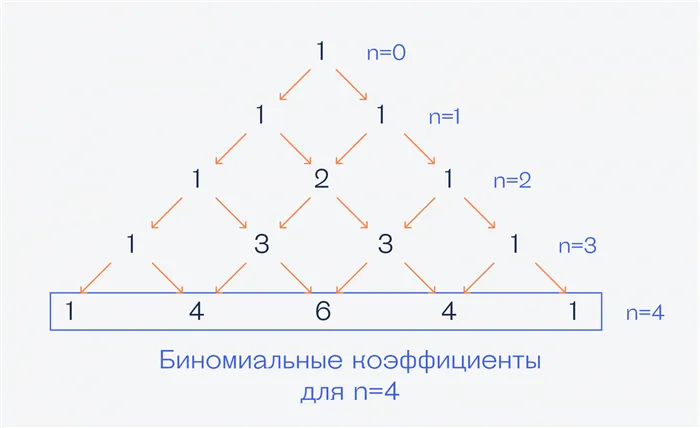
Символ S, который мы уже упоминали, является символом суммы, а числа в больших скобках — биномиальными коэффициентами. В общем случае они рассчитываются следующим образом:

Исходя из этой адской формулы, чтобы вычислить биномиальное число в компьютере, нужно несколько раз посчитать факториал — который является произведением всех целых чисел от единицы до определенного числа. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120. Кроме того, факторы занимают много памяти из-за своей циклической природы. Может оказаться, что мы не можем вычислить биномиальные коэффициенты, потому что у нас больше нет рабочей памяти.

Однако оказывается, что считать коэффициенты не обязательно — есть более простой способ.

Древние знания

Особые случаи биномиальных теорем известны примерно с четвертого века до нашей эры, когда знаменитый греческий математик Евклид сообщил об особом случае биномиальной теоремы

В шестом веке нашей эры индийские математики, вероятно, знали способ выразить общее правило в виде специального правила и выразили его примерно в такой форме: n! / (n — k)!k! Явное утверждение содержится в тексте Бхаскара, датируемом XII в. Насколько известно, первая формулировка биномиальной теоремы и соответствующей матрицы коэффициентов содержится в работе аль-Караджи, которую цитирует в своих трудах ас-Самавал.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов и представил доказательство теоремы бинома и треугольного правила Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя большая часть его математических работ не дошла до современных ученых.

Биномиальные разложения малой силы были известны в математических работах Ян Хуэя и Чу Ши-Цзе в 13 веке. Ян Хуэй ссылается на более ранний текст Цзя Сяня 11 века, но эти записи также утрачены сегодня.

В 1544 году Михаэль Штифель ввел термин «биномиальный коэффициент» и показал, как его можно использовать для выражения (1 + a) n в терминах (1 + a) n — 1 через треугольник Паскаля. Блез Паскаль подробно изучил треугольник в своем трактате «Traité du triangle arithmétique» (1653).

Структура чисел уже была известна, в частности, европейским математикам позднего Возрождения:

Сокращение дробей. Что значит сократить дробь. Как сократить дробь 6 класс?

Кстати, Исааку Ньютону обычно приписывают обобщенную биномиальную теорему, которая применима к любой рациональной экспоненте.

Стифеля.
Никколо Фонтана Тарталья.
Симона Стевина.

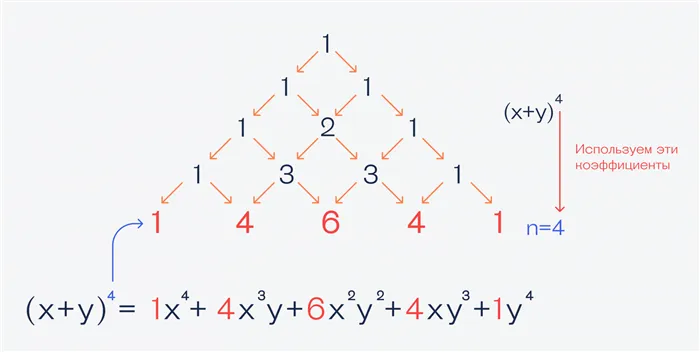
Согласно теореме, любую степень x + y можно разложить в сумму вида (x + y) n = ( n ₒ) x n y 0 + ( n 1) x n — 1 y 1 + ( n 2) x n — 2 y 2 + — + ( n n n — 1) x 1 y n — 1 + ( n n n) x 1 y n — 1 + ( n n n) x 0 y n, где каждое ( n k) — целое положительное число, называемое коэффициентом биномиального числа.

Утверждение теоремы

Если экспонента равна нулю, соответствующее степенное выражение принимается за 1, и этот мультипликативный коэффициент часто исключается из формулы. Нередко правая часть уравнения записывается в виде ( n ₒ) x n + —. Эта формула также называется биномиальным тождеством.

Простейшим примером биномиальной формулы Ньютона является решение квадрата x + y, например, (x + y) 2 = x 2 + 2xy + y 2. Биномиальные коэффициенты 1, 2, 1, которые появляются в этом разложении, соответствуют второй строке треугольника Паскаля. Здесь следует придерживаться общепринятых правил, в которых верхняя «1» треугольника принимается за 0-линию.

Коэффициенты высших сил x + y соответствуют нижним линиям треугольника Паскаля. В расчетах прослеживаются различные закономерности. В общем случае для разложения (x + y) n :

Теорему можно применить к степени любого бинома.

степени x уменьшаются на 1 в каждом члене, начинаясь с n до достижения 0 (при x 0, равном 1);
y начинаются с 0 и увеличиваются на 1 (пока не достигнут n степени);
число слагаемых в разложении перед объединением одинаковых слагаемых является суммой коэффициентов и равно 2 n ;
после объединения одинаковых слагаемых в разложении получится n + 1.

Для

С точки зрения геометрии

В бесконечно малом исчислении геометрическое доказательство бинома Ньютона выглядит следующим образом: (x n )′ = nx n-1. Если задать a = x, b = ∆x и интерпретировать b как бесконечно малую переменную a, то получится следующая картина: бесконечно малая переменная объема n-мерного гиперкуба (x + ∆x) n, где линейный член (в ∆x ) равен nx n-1, площади n граней, каждая из которых имеет размерность (n — 1), (x + ∆x) n = x n + nx n-1 ∆x + ( n 2)x n-2 (∆x) 2 + — .

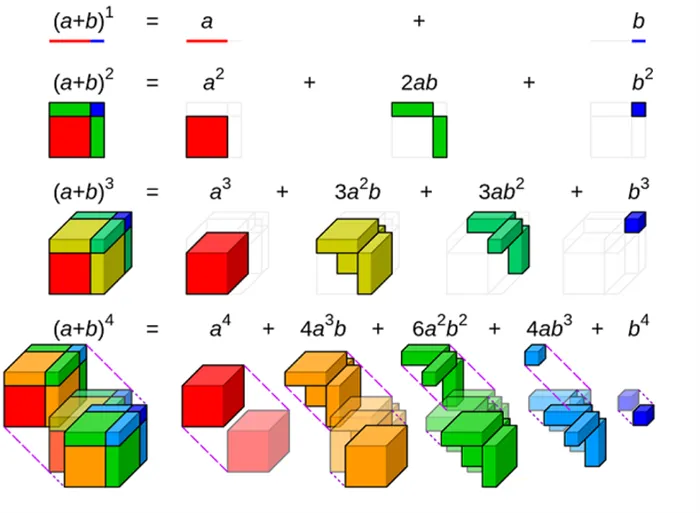
Подставив это уравнение в определение производной по разности и взяв пределы, члены высшего порядка, (∆x) 2 и выше, становятся несущественными, и получается формула (x n )′ = nx n-1. Все это интерпретируется так: «Бесконечно малая скорость изменения объема куба n при изменении длины его сторон равна площади n (n — 1)».

Биномиальные коэффициенты появляются в расширении бинома Ньютона. Обычно они записываются как ( n k) и интерпретируются как количество способов выбрать k элементов из n ряда треугольника Паскаля. Коэффициент x n — k y k определяется по формуле ( n k) = n! / k! (n-k)! который задается факториальной функцией n!

Существует несколько доказательств этой теоремы. Например, мы можем рассмотреть комбинаторику. Его алгоритм является одним из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Расчет выглядит следующим образом, поскольку есть три линии x и y, а именно xyyy, yxy, yyx. Они соответствуют трем подмножествам двух элементов из, а именно, ,, ,, , где каждое подмножество определяет положение y в соответствующей строке треугольника.

(x + y) (x + y) (x + y);
xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy;
x 2 + 3x 2 y + 3xy 2 + y 3 равняется ( 3 2) = 3.

Или, например, общий случай. Разложение (x + y) n дает сумму 2 n слагаемых вида e1 e2. en, где каждое ei равно x или y. Коэффициенты транспонирования показывают, что каждое произведение равно x n — k y k для k от 0 до n. Для данного k следующие значения равны по порядку:

Докажите биномиальную теорему либо по определению, либо с помощью короткого комбинаторного аргумента, когда ( n k) представляется в виде n! / k! (n-k)!

количество копий x n — k y k в расширении;
количество n — символов x, y строк, имеющих y ровно в k позициях;
количество k-элементных подмножеств .

В этом видеоуроке мы вспомним комбинации, называемые комбинаторами. Мы вспомним формулу для подсчета количества комбинаторов, а также свойства комбинаторов. Мы познакомимся с биномиальной формулой Ньютона. Назовите так называемый треугольник Паскаля. Давайте ознакомимся со свойствами элементов последовательности треугольника Паскаля.

Бином Ньютона

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный кабинет.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

2. Распространите видеоуроки в своих личных кабинетах среди учеников.

На сегодняшнем уроке мы вспомним, какие соединения называются комбинациями. Запомните формулу для подсчета количества комбинаций и для того, чтобы

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Бином Ньютона»

Эту формулу часто называют просто биномом Ньютона. Он применим к любой натуральной величине, так называемым биномиальным коэффициентам, которые можно определить по следующей формуле.

Что такое функция в алгебре. Что такое функция в алгебре?

Давайте воспользуемся этой формулой для увеличения биномиального числа
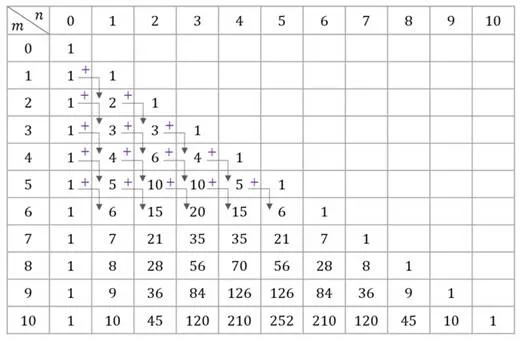
В общем случае биномиальные коэффициенты легко найти с помощью так называемого треугольника Паскаля.
Треугольник Паскаля — это матрица значений с

Теперь вы увидите участок треугольника Паскаля, показывающий, как получить определенные члены матрицы на основе свойства итерирующих комбинаций.

Обратите внимание, что треугольник Паскаля можно произвольно расширить.
Эта таблица наглядно иллюстрирует первое известное нам свойство комбинаций. Его можно сформулировать следующим образом: Числа, равноудаленные от концов ряда треугольника Паскаля, равны.

Теперь запишем развитие биномиального числа

Обратите внимание, что экспонента бинома равна пяти. А число членов многочлена равно шести, значит, на один больше.

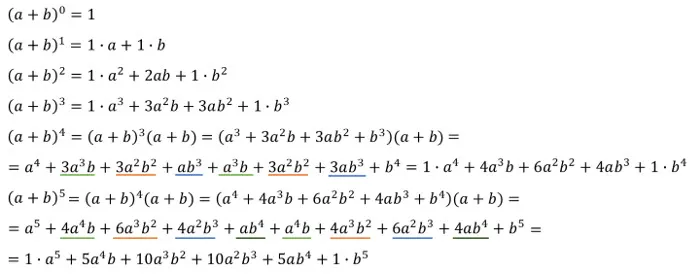
Экспонента первого члена, т.е. до, увеличивается на единицу от до

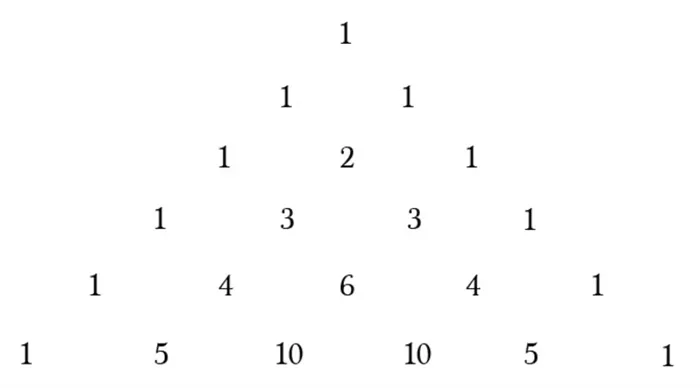
Также обратите внимание, что биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны.
Поэтому при написании экспоненты бинома полезно учитывать следующее:

1) число членов полученного многочлена на единицу больше экспоненты EM степени бинома, т.е. равно

2) экспонента первого полинома постепенно уменьшается на единицу от, а экспонента второго полинома стабильно увеличивается на единицу от до

3) Биномиальные коэффициенты, которые, согласно биномиальной формуле Ньютона, равноудалены от начала и конца разложения, равны.

Биномиальное разложение содержит на один член больше, чем экспонента биномиальной степени.

Все члены разложения имеют одинаковую размерность относительно букв a и b, что соответствует экспоненте бинома. (Размерность монома относительно букв a и b равна сумме экспонент мощностей этих букв, входящих в состав монома).

Поскольку все члены в разложении имеют одинаковую размерность относительно букв a и b, это разложение является однородным многочленом относительно букв a и b (см. стр. 450).

В разложении экспонента буквы a последовательно уменьшается на единицу, начиная с экспоненты n, а экспонента буквы b последовательно увеличивается на единицу, начиная с экспоненты, равной нулю.

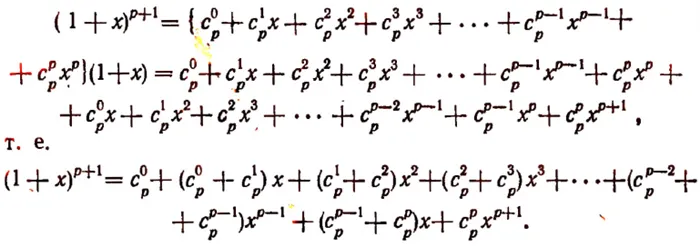
называется формулой общего члена разложения, поскольку, задавая букву k целыми значениями от 0 до n, можно получить любой член разложения.

Теперь запишем разложение выражения

Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны. Согласно первому свойству числа комбинаций мы имеем на самом деле:

2. сумма биномиальных коэффициентов равна числу 2, увеличенному на экспоненту биномиальной степени.

Доказательство:

Предположим, что биномиальная формула.

Свойства разложения бинома

3. сумма биномиальных коэффициентов на четных местах равна сумме биномиальных коэффициентов на нечетных местах.

Доказательство:

Предполагая, что в тождестве.

С левой стороны мы имеем следующее:

Член разложенияявляетсячленом разложения и обозначается символом

Мы должны были это доказать.

Если подставить их значения вместо биномиальных коэффициентов, то биномиальная формула Ньютона примет вид:

Свойства биномиальных коэффициентов

Для простоты принято записывать биномиальную формулу Ньютона в следующей символической форме:

Читатель может не понять, почему такая элементарная формула должна быть

где n — целое положительное число, названа в честь великого ученого Ньютона, тем более что эта формула была известна еще до Ньютона. Аль-Каши (пятнадцатый век), например, знал его, и мы находим его в работах Паскаля. Это объясняется тем, что именно Ньютон обобщил эту формулу на любую вещественную экспоненту.

Ньютон был первым, кто показал, что выражение

где и

Следующая таблица

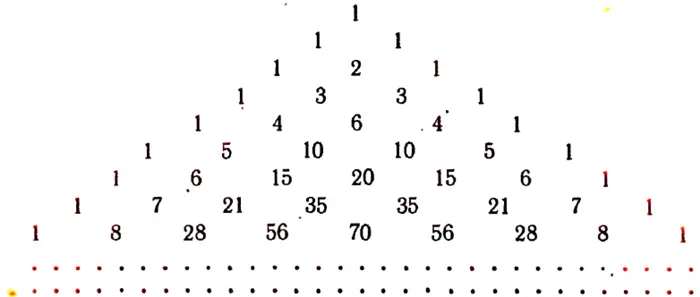
называется треугольником Паскаля*.

По бокам этой матрицы расположены единицы, а внутри — числа, которые получаются в результате сложения двух соответствующих чисел из предыдущего ряда. Например, число 21 в ряду 8 получается в результате сложения чисел 6 и 15 над ним.

n-я степень биномиального числа. Например:

Треугольник Паскаля получается из следующей таблицы:

из-за того, что

Треугольник Паскаля содержится в книге Паскаля «Трактат об арифметическом треугольнике», опубликованной после его смерти в 1665 году.

Примерно в 1665 году Исаак Ньютон обобщил свою теорему о биноме. Он сделал это, чтобы решать задачи для действительных экспонент в дополнение к неотрицательным целым числам. В этом обобщении конечная сумма заменяется бесконечным рядом. Для этого коэффициентам бинома нужно присвоить произвольный старший индекс, что невозможно при использовании обычной формулы с номерами коэффициентов.

r равен нулю, поэтому это уравнение сводится к обычной биномиальной теореме, где существует не более r + 1 ненулевых членов. При других значениях r ряд обычно имеет бесконечно много ненулевых членов.

Примеры разложения многочленов на множители. Как разложить на множители?

| y | и определите степени x + y и x, используя голоморфную ветвь логарифма на открытом диске радиуса | x | в центре x. Обобщенная биномиальная теорема также применима к элементам x и y в алгебре Банаха, если x = y, x инвертируема и || y / x |||.

Арифметический треугольник, или треугольник паскаля

Биномиальная теорема может быть обобщена для рассмотрения степеней суммы с более чем двумя членами. Теорема полиномов часто полезна при работе в нескольких измерениях для работы с произведениями биномиальных выражений.

Лучше всего начать с решения простой задачи, которую учитель покажет классу на уроке алгебры. Например, вам нужно расширить (2x-3)³. Это несложно сделать с помощью электронного калькулятора. Но вы должны использовать биномиальное число, когда имеете дело с большими расширениями, такими как бипоследовательности, которые увеличиваются до 4, 5, 6, …. степени.

Сначала необходимо определить два члена бинома (позиции x и y в формуле) и степень (буква n), до которой вы хотите расширить бином. Например, чтобы разложить (2x-3)³, два члена равны 2x и-3, а сила (или n) равна 3. Следует отметить, что всякий раз, когда в биноме есть символ вычитания, очень важно помнить, что знак минус должен использоваться только как отрицательный символ в связанном члене.

Замечательная теорема биномов заключается в том, что она позволяет найти расширенный многочлен, не перемножая ряд биномов вместе. Довольно интересная недвижимость. Оказывается, что число членов в расширяющемся многочлене, который мы ищем, всегда на единицу больше, чем мощность, которую нужно расширить. Это означает, что нам нужно составить многочлен с четырьмя членами, так как мощность в данном примере равна 3.

Каждый член имеет (2x) и (-3) и формулу «n выбирает k», где n = 3. Нам нужно написать это 4 раза, по одному разу для каждого члена, где значение k находится в «n выбирает k». Значения нот на этом этапе счета не заполняются.

Затем нужно ввести k-значения и мощности. Здесь вы можете следовать формуле суммирования и увеличивать мощность для каждого члена. Но следовать выкройкам довольно легко. Значения k в «n выбирает k» начинаются с k = 0 и увеличиваются на 1 в каждом члене. Последний член должен заканчиваться n равным k, поэтому n = 3 и k = 3. Далее нужно сложить силы в (2x) и (-3).

Включение (2x) начинается со значения n, в данном случае 3, и уменьшается на 1 для каждого члена, пока не достигнет нуля. Включение (-3) начинается с нуля и увеличивается на единицу для каждого члена, пока не достигнет n или 3 в данной задаче. Это решает половинный случай: (³ₒ)(2x)³‾⁰˭³ (-3)⁰ + (³1)(2x) 3-1=2 (-3) 1 + (³2)(2x) 3-2=1 (-3) 2 + (³3)(2x) 3-3=0 (-3) 3 .

Биномные обобщения

Поскольку любое значение, возведенное в ноль, равно 1, мы можем упростить суммы с нулевой силой. Затем, идя дальше и применяя силы, имеет смысл упростить все возможные комбинации.

Однако для произвольного числа r можно вычислить ( r k) = r(r — 1) ··· (r — k + 1) / k! = (r)k / k!, где (·) k является символом Похгаммера, который здесь означает падающий факториал. Это согласуется с обычными определениями. Когда r — неотрицательное целое число, биномиальные коэффициенты при k>Последняя часть должна решить формулу комбинации. Самый очевидный способ сделать это — применить формулу комбинации к каждой проблеме. Однако стоит попробовать пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путем формирования треугольника с тремя начальными единицами. Затем для каждой строки просто напишите 1 на обоих концах и найдите среднее значение, сложив два значения вверху.

Обобщения можно распространить на случай, когда x и y — комплексные числа. Для этой версии следует снова принять | х |>Теперь о хорошем. Все ответы скрыты в треугольнике Паскаля — это настоящая шпаргалка. На диаграмме ниже показано, где находятся скрытые «n пик k».

Для этой конкретной задачи нам нужно решить: 3 пики 0, 3 пики 1, 3 пики 2 и 3 пики 3. Все эти значения содержатся в четвертом ряду. Поэтому нам остается только посмотреть на четвертый ряд треугольника и сделать выводы, сравнив ответы. Четвертый ряд имеет следующие значения: 1, 3, 3, 1. Таким образом, нам нужно только заменить n на выбор k, и мы получим следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Проверка в действии

Наконец, остается только перемножить каждый член и упростить его до простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что силы каждого члена по-прежнему увеличивают степень исходного бинома.