Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Шкалы. Координатный луч
В этом уроке мы поговорим о том, что такое линейка, где ее найти, а также о том, что такое координатный пучок и координаты.
Линейка используется для измерения длины прямой линии. Измерение возможно благодаря тому, что линейка несет на себе шкалу — на ней нанесены штрихи через равные промежутки времени.
Обычно расстояние между штрихами на школьной линейке составляет 400 мм, это называется шагом.
Сантиметровые интервалы также отмечены на линейках — под продольными линиями есть цифры. Сантиметровый отрезок содержит 10 долларов по 400 мм.
Шкала — это ряд отметок (делений), расположенных в определенном порядке, которые соответствуют числовому значению измеряемого размера.
Вы также можете увидеть шкалу на термометре. Шкала обозначает один градус и цифры 10, 20, 30 градусов и т.д.

Вы также можете увидеть шкалу на весах. Как правило, одна отметка на шкале соответствует 100 г. Цифры обозначают значения 400, 2, 3 кг и т.д. Помните, что $400 килограммов = $1 000 граммов.
Однако, когда необходимо взвесить крупные предметы, используются весы с делениями более 100$ g. В этом случае используются такие единицы массы, как тонны и сантиметры.
400$ т называется 400$ т, 400$ т = 1000$ кг 400$ центнер называется 400$ с, 400$ с = 100$ кг.
Координатный луч
В математике масштаб можно найти в координатном радиусе. Давайте подробно рассмотрим, что такое этот радиус и как его построить.
Нарисуем радиус OX, как показано на рисунке 4.
Точка О является его началом. Она соответствует числу
Координаты
Числа, соответствующие точкам на координатном луче, называются координатами этих точек. Мы говорим, что точка O имеет координаты $, а точка E имеет координаты $400. Она написана следующим образом: O$(0)$, E$(1)$.
На координатном луче отметим точки A$(2)$, B$(3)$, C$(4)$ — рисунок 6. Это дало нам масштаб на координатном луче, который можно продолжать бесконечно.
$. Проведите отрезок 400$$ см от точки O вправо и отметьте полученную точку E (Рисунок 5).
Точка E будет соответствовать числу 400$. Сегмент OE называется сегментом единицы.
Таким образом, радиус OX стал координатным радиусом, где O — начало координат, а OE — единичный отрезок. В нашем примере единичный отрезок равен 400$ см, но он может иметь любую длину, за исключением того, что за единицу принимается длина в координатном луче.
Координатный луч — это луч, который имеет опорную точку, опорное направление и единичный сегмент.
Что такое координатный луч?
Координатный луч — это средство ориентации на плоскости.
Каждый координатный луч имеет:
- Начало координат
- Единичный отрезок и шкала
- Направление движения
Направление движения обычно указывает направление, в котором поднимаются маркеры.
С помощью координатного луча можно определить положение точки только вдоль прямой линии. Значение. Представим координатный луч в виде реки. Таким образом, мы можем определить местоположение путника по реке, но не можем сказать, как далеко вглубь страны он зашел.
По этой причине вместо координатной прямой обычно используется декартова система координат.
Когда-то моряки добавили в систему координат угол, под которым точка возвышается над линией горизонта. Так родилась полярная система координат. Это одна из старейших навигационных систем в мире.
Однако координатная линия используется для чертежей при решении задач, поэтому она до сих пор используется в курсах математики.
Чем отличается координатный луч от координатной прямой?
Ранее мы уже говорили о координатной линии. Мы должны сразу различать координатный луч, числовой луч и координатную линию.
Координатный луч и луч числа очень похожи. Разница в том, что числовой луч может начинаться в любой точке, и эта точка является его началом. Все зависит от того, какие цифры мы имеем для сравнения. Координатный луч всегда начинается с 0, иначе его нельзя считать координатным лучом.
Координатная линия, в отличие от координатного луча, может простираться как вправо, так и влево от начала координат. Это позволяет отмечать на координатной линии отрицательные числа.
Чтобы отметить отрицательные координаты на координатном луче, необходимо построить другой луч, направленный влево.
Область применения
На самом деле, окружность координатного луча довольно мала. Это может быть:
- Рисунки к задачам
- Сравнение положительных или отрицательных чисел. Причем либо только положительных, либо только отрицательных
- Использование для отметки координат. Но декартова система куда удобнее. Хотя нельзя забывать, что декартова система представляет собой 4 координатных луча
Это действительно одна из самых гениальных идей в математике: соединить 4 координатных луча, чтобы получить систему ориентации на плоскости. Два луча лежат на одной прямой и направлены в противоположные стороны, а два других луча лежат на прямой, перпендикулярной первому лучу, и также направлены в противоположные стороны.
В результате получилась система, которая используется для ориентации на плоскости уже несколько сотен лет. Кроме того, декартову систему можно перевести в пространство.
Спутниковые системы, радары и автомобильные навигационные системы используют эту навигационную систему. Художники используют эту систему при работе с компьютерной графикой. И именно с пучка координат все началось. Поэтому нельзя сказать, что он бесполезен. Пучок небольшой по размеру, но он положил начало современным навигационным системам.
Решение:
Известно, что число, соответствующее точке на координатном луче, является координатой этой точки. Точка E соответствует числу 1, а длина прямой OE считается единицей длины и называется единичной прямой.
Из начала координат O в точку C ведут 2 единичных отрезка. Поэтому точка C соответствует числу 2, то есть координате точки C(2). Ответ: координата точки C(2).

Пример 4: Напишите число на конце стрелки на рисунке.
Решение:
Чтобы найти число на конце стрелки на заданном рисунке, составьте числовое выражение и найдите его значение:
Значит, число, соответствующее точке на конце стрелки, равно 56. Ответ: Число на конце стрелки на диаграмме равно 56.
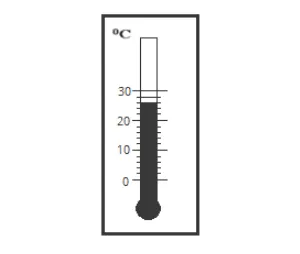
Пример № 5: Какую температуру показывает термометр на диаграмме? Какую температуру показывает термометр, когда стрелка опускается на 3 ступени?
Решение:
Из анализа этого рисунка можно сделать вывод, что 1 деление соответствует 2° C.
— Это интересно! Давайте рисовать вместе.
— Давай! Вместе веселее.
И мальчики начали рисовать картину.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
— 1…, 2…, 3…, 4…, 5…, 6…, 7…, 8…, 9…, 10…, 11… и 12…

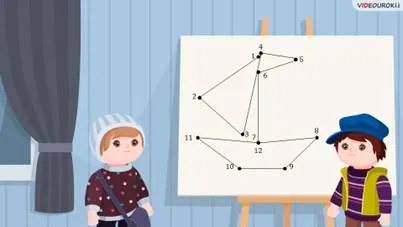
— Саша, смотри, у нас есть корабль! — Паша был в восторге.
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Шкала. Координатный луч»
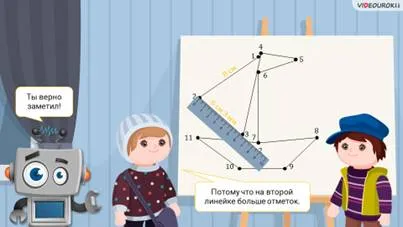
— Точно! — Саша заметил. Но мы все равно должны вычислить сумму длин всех получившихся отрезков. Поэтому мы должны измерить их линейкой.
— Саша, что-то не так с твоей линейкой! — отметил Паша. — Мы не можем измерить длину отрезков с помощью этой линейки.
— Но у меня нет другой линейки. Что мне делать? — Разочарованный Саша.
— Я думаю, Электроша знает, что делать, — предложил Паша.
— «Мальчики, прежде чем я помогу вам измерить детали, я хочу, чтобы вы разогрелись и сделали несколько оральных упражнений», — предложил Электроша.

— Давайте сравним! Посмотрите, что вам следовало взять!
— Вернемся к вашей проблеме, — продолжал Электроша, — вы не можете измерить длину отрезков, потому что ваша линейка не имеет достаточного количества делений.
— Что значит не хватает секций? — удивился Саша. — У моего правителя есть разделения.
— «У тебя есть деления, — сказал Джошуа, — но посмотри, когда ты измерил длину второго сегмента, ты не смог отметить длину второго сегмента. Вы обнаруживаете, что его длина больше 6 сантиметров, но не можете измерить его более точно. Совсем другое дело, если бы мы измеряли длину того же отрезка линейкой, как сейчас.
— Теперь я понимаю, что ты имеешь в виду», — радовались мальчики.
— Видишь, расстояние одинаковое, а результаты более точные», — сказал Елетроша». — Почему вы так думаете?
— Может быть, потому что на второй линейке больше знаков, — предположил Паша.
— Вы правы», — сказал он.

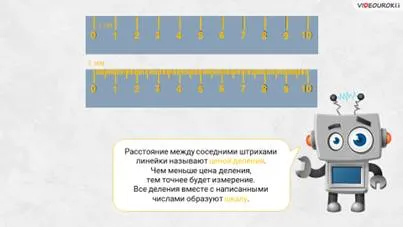
Давайте рассмотрим этих двух правителей поближе. Посмотрите, на одной линейке и второй линейке есть отметки и неровности. Все неровности равноудалены друг от друга. Есть цифры, которые находятся рядом с некоторыми штрихами. Легко заметить, что все штрихи на их линейках разделены на равные части. Эти части называются сегментами.
— А теперь скажите, какое расстояние между соседними штрихами первой и второй линейки», — спросили дети у «Электроса».

— Расстояние между соседними штрихами первой линейки — 1 см, а второй — 1 мм, — ответил Саша.
— Электрошкала подтвердила. Это расстояние называется значением масштаба. Чем меньше значение шкалы, тем точнее будет измерение. Все деления вместе с написанными на них цифрами образуют шкалу.