Нечетные числа можно узнать по специальным буквам, используемым для их обозначения, или по записи их в виде десятичных чисел без окончания. Выражения этого типа можно легко отличить по наличию корня. С этими величинами можно производить те же операции, что и с другими вещественными числами. Их можно умножать, складывать, сравнивать и так далее.
Иррациональные числа
Если при решении математической задачи получается дробь, в которой числитель не может быть полностью разделен на знаменатель, то это иррациональное число.
Есть еще одно условие для того, чтобы такая дробь была иррациональным числом. Это отсутствие точек в последовательности цифр после десятичной точки, т.е. нет периодической последовательности чисел.
Иррациональное число — это число, которое не может быть представлено как полный коэффициент деления двух целых чисел.
Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать значительных проблем (вплоть до отчисления). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Даже математикам древности приходилось сталкиваться с таким разнообразием. Для них, например, было ясно, что диагональ квадрата нельзя разделить на длину его сторон, чтобы получить дробь, которая не является бесконечной. Аналогичным образом характеризуется отношение постоянной π выбранной окружности к ее диаметру.
Проще говоря, если обычная десятичная дробь имеет бесконечное число десятичных знаков и не содержит повторений периода, то она является представителем иррационального множества.
Чтобы понять это, мы можем обратиться к примерам: √2 = 1,41421356. ; -√11= -3.31662…; π = 3,1415926.
Термин для обозначения этой категории чисел состоит из двух частей: ratio, что означает «пропорция», и ir, что означает «отрицание». Поэтому слово «иррациональный» было зарезервировано для дробей, которые не дают определенного соотношения.
Например, диагональ квадрата, сторона которого равна 1, не может быть представлена рациональным числом, но имеет определенное числовое выражение. К таким случаям также относятся √5, √7, √10. Для выражения таких значений был введен набор иррациональных чисел, каждое из которых может быть представлено бесконечной непериодической дробью (в отличие от рациональных чисел, которые могут быть представлены периодической десятичной дробью).
Виды, место в общей классификации, как обозначаются
В числовой классификации иррациональные числа занимают четкое место рядом с рациональными, которые делятся на целые и дробные.
Буква I используется для обозначения количества. Математическое выражение выглядит следующим образом.
Алгебраические и трансцендентные
В алгебре множества, которые могут быть квадратными корнями с целыми коэффициентами многочленов, принадлежат алгебраическому множеству. Те, кто не может выступать в этой роли, образуют другую группу — трансценденты.
Происхождение термина «трансцендентальный» объясняется его переводом с латыни: transcendentis — выходящий за пределы. Таким образом, эти величины находятся вне множества чисел, которые могут быть квадратным корнем из целого коэффициента различных полиномов.
Впервые о необходимости такого набора упомянул Леонгард Эйлер в 1775 году. Стоит отметить, что во времена его творчества трансцендентальные ценности еще не были известны.
Математики не могли вычислить их парадигму в течение многих лет. Только в 1844 году Дж. Луисвилл передал всем свою парадигму. Его теорема стала новаторской для теории диофантовых приближений.
Алгебраические числа минимально аппроксимируются рациональными числами, в частности, если алгебраическое число αn (n — наименьшая степень многочлена P(x) с целыми коэффициентами такого, что P(α)=0), то для любой дроби p/q имеет место выражение:
Где C — константа, зависящая от α.
Все числа вида m/n, для которых n не равно нулю, а m и n представлены целыми числами, являются алгебраическими. Для них выполняется равенство: nx-m=0.
Помимо рациональных чисел, алгебраические числа также включают иррациональные числа, которые характеризуются формулой n √m. В данном случае m и n представлены целыми числами, причем n больше или равно 2.
При любой операции с алгебраическими числами (сложение, вычитание, деление или умножение) результатом является алгебраическая величина. Более того, корни многочленов, коэффициенты которых также принадлежат этому множеству, являются алгебраическими.
Для чего они используются
В математике использование иррациональных чисел объясняется перечнем их свойств. Например, не всегда нужно точно определять значение, получаемое квадратным корнем из 2. В геометрии, например, длина гипотенузы часто измеряется только приблизительно (1,4, 1,41 и т.д.). Точное выведение квадратного корня из 2 необходимо только при работе с абстрактной математической моделью.
Однако такие ситуации существуют в науке. Поэтому существование множества иррациональных чисел оправдано. Их можно использовать для вычисления части Дедекинда в рациональных числах, где наибольшая часть отсутствует в нижней части, а наименьшая — в верхней.
Представители иррациональных величин позволяют сжать числовую линию с нанесенными рациональными величинами, так что между каждой такой парой можно написать иррациональную.
Бывают случаи, когда сложение двух иррациональных значений приводит к рациональному значению.
Например, сложение корня из семи (любой степени) и такого корня из семи, только со знаком минус, приводит к рациональному числу, а именно 0.
Сумма двух положительных иррациональных чисел также может быть рациональным значением. Однако сложение рационального и иррационального числа всегда приводит к представительному иррациональному числу. Это свойство называется незамкнутостью множества.
Можно сделать вывод, что введение набора иррациональных чисел необходимо для повышения точности. Например, когда между натуральными числами один и два не было промежуточных значений, необходимо было ввести их, чтобы расширить диапазон точности.

Определение иррациональных чисел
Иррациональное число — это действительное число, которое не может быть выражено в виде деления двух целых чисел, то есть в виде рациональной дроби:
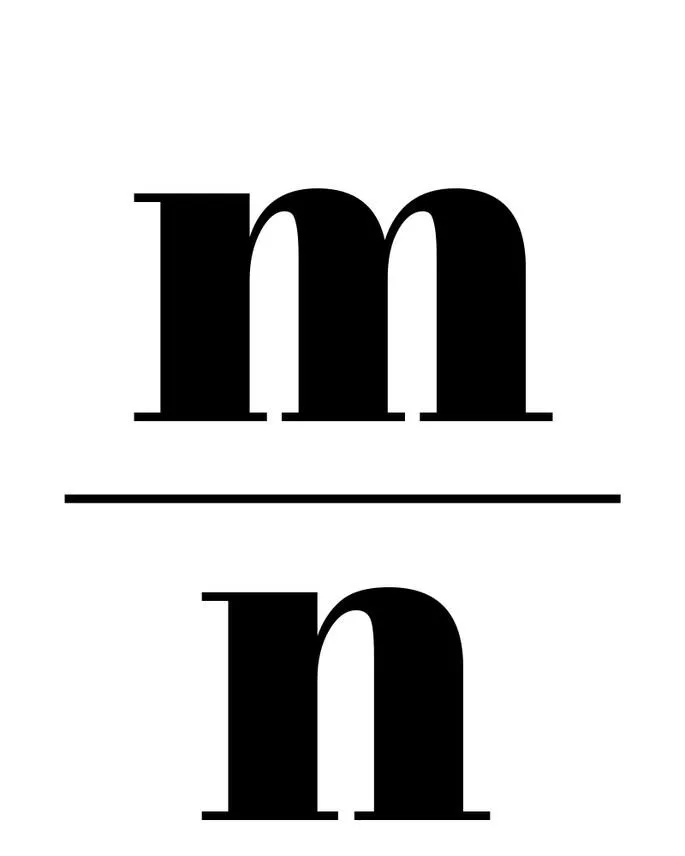
Она может быть выражена в виде бесконечного непериодического десятичного числа.
Бесконечное ni
Онлайн-подготовка к GCSE по математике — отличный способ снять стресс и закрепить свои знания перед экзаменом.
- π = 3,1415926.
- √2 = 1,41421356.
- e = 2,71828182…
- √8 = 2.828427.
- -√11= -3.31662…
Теперь давайте рассмотрим противоположное определение этой темы.
Рациональное число — это число, которое может быть представлено в виде положительной или отрицательной дроби или в виде нуля. Если число можно получить путем деления двух целых чисел, то оно является в точности рациональным числом.
Рациональные числа — это числа, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.

Свойства иррациональных чисел
Рациональные числа — это все натуральные числа, целые числа, обычные дроби, бесконечные периодические дроби и конечные десятичные числа.
Множество рациональных чисел обычно обозначается латинской буквой Q.
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Примеры рациональных чисел:
Определение рациональных чисел
Рациональные числа имеют определенные закономерности и определенные свойства — рассмотрим каждое из этих свойств. Пусть a, b и c — любые рациональные числа.
Основные свойства операций с рациональными числами
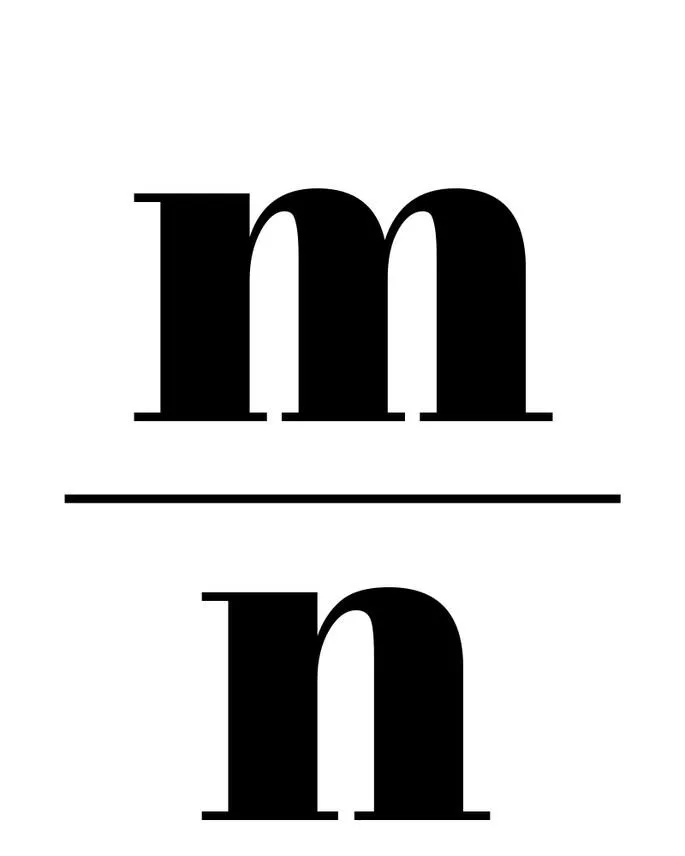
- десятичная дробь 1,15 — это 115/100;
- десятичная дробь 0,2 — это 1/5;
- целое число 0 — это 0/1;
- целое число 6 — это 6/1;
- целое число 1 — это 1/1;
- бесконечная периодическая дробь 0,33333. — это 1/3;
- смешанное число
- отрицательная десятичная дробь -3,16 — это -316/100.
- Переместительное свойство сложения: a + b = b + a.
- Сочетательное свойство сложения: (a + b) +c = a + (b + c).
- Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a.
- У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0.
- Переместительное свойство умножения: ab = ba.
- Сочетательное свойство умножения: (a * b) * c = a * (b * c).
- Произведение рационального числа и едины не изменяет это число: a * 1 = a.
- У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1.
- Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.








