Сравним отрезки: QL>FJ (т.к. 5>3), FJ
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками на этой прямой. Точки, определяющие границы прямой, называются концами отрезка.
Отрезок прямой обозначается двумя заглавными латинскими буквами на его концах: Секция AB или BA .
Длина отрезка
Длина отрезка прямой — это расстояние между его концами. Все сегменты больше нуля:
Длина отрезка измеряется путем сравнения длины отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого считается равной единице. Поэтому:
Длина отрезка — это положительное число, которое показывает, сколько раз единичный отрезок и его части помещаются в этот отрезок.
Часто встречаются единичные отрезки размером 1 мм, 1 см, 1 дм, 1 м или 1 км. Длину отрезка можно измерить линейкой или другим прибором для измерения длины:
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
- Длины равных отрезков равны.
- Любой отрезок имеет определённую длину, большую нуля.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Свойства равных отрезков одинаковы.
Пример. Возьмите два отрезка CD и LM:
Если расположить отрезки параллельно друг другу так, чтобы точка C лежала над точкой L, то мы увидим, что точка D лежит над точкой M:
Длина отрезков равна, поэтому CD = LM.
Как сравнить два отрезка без линейки
Если отрезки проведены из клеток, мы можем измерить клетки. Однако это не всегда так. Если квадратов нет, можно воспользоваться компасом. Сначала поместите раствор циркуля на концы одного сегмента, а затем, не перемещая ножки, поместите иглу на конец другого сегмента и проверьте, шире или уже второй сегмент раствора циркуля.
Если у вас нет компаса, вы можете сделать своеобразную линейку из полоски бумаги. Вам не нужно рисовать деления. Вам нужно только отметить начало и конец одного деления, затем сделать отметку в начале второго деления и сравнить их.
Таким образом можно даже сравнивать деления, нарисованные на земле, например, чтобы отметить места для скамеек на одинаковом расстоянии от стены дома. Но в этом случае нужно использовать уже не полоску бумаги, а доску или веревку.
Как сравнить два отрезка в координатной сетке
Чтобы сравнить отрезки, необходимо знать их длину. В этой статье мы объяснили, как найти длину отрезка прямой, заданную координатами на плоскости или в пространстве. Рассмотрим следующие отрезки на плоскости с координатами: отрезок a = и отрезок b = .
Конечно, очевидно, что второй интервал короче первого, но в математике «очевидно» не считается, это нужно доказать. Поэтому мы напишем формулу для вычисления длин отрезков и придадим координатам числовое значение. После этого вы сможете легко объяснить, как сравнить два отрезка.
- Длина отрезка а d1 = √((х 1 — х 2)² + (у 1 — у 2)²)
- Длина отрезка b d2 = √((х 3 — х 4)² + (у 3 — у 4)²)
Пусть x 1 = -6, y 1 = 5, x 2 = 4, y 2 = -3, x 3 = -2, y 3 = -4, x 4 = 1, y 4 = -2. Означает:
- d1 = √((х 1 — х 2)² + (у 1 — у 2)²) = d1 = √(((-6) — 4)² + (5 — (-3))²) = √((-10)² + 8²) = √164
- d2 = √((х 3 — х 4)² + (у 3 — у 4)²) = √(((-2) — 1)² + ((-4) — (-2))²) = √((-3)² + 2²) = √13
- √164>√13, значит, d1>d2.
Аналогично можно сравнивать отрезки в трехмерных координатах, только тогда нужно учитывать третью координату: отрезок a = и отрезок b = .
Формулы аналогичны тем, которые мы написали для координатной сети на плоскости:
- Длина отрезка а d1 = √((х 1 — х 2)² + (у 1 — у 2)² + (z 1 — z 2)²)
- Длина отрезка b d2 = √((х 3 — х 4)² + (у 3 — у 4)² + (z 3 — z 4)²)
Пусть x 1 = -6, y 1 = 5, z 1 = 1, x 2 = 4, y 2 = -3, z 2 = 2, x 3 = -2, y 3 = -4, z 3 = 3, x 4 = 1, y 4 = -2, z 4 = -11.
- d1 = √((х 1 — х 2)² + (у 1 — у 2)² + (z 1 — z 2)² = √(((-6) — 4)² + (5 — (-3))² + (1 — 2)²) = √((-10)² + 8² + (-1)²) = √165
- d2 = √((х 3 — х 4)² + (у 3 — у 4)² + (z 3 — z 4)²) = √(((-2) — 1)² + ((-4) — (-2))² + (3 — (-11))²) = √((-3)² + 2² + 14²) = √(9 + 4 + 196) = √209
- √209>√165
Поэтому в данном случае вторая часть больше первой.
Помните, прямой участок. Это отрезок прямой линии, ограниченный с обеих сторон точками. Предположим, есть два отрезка, параллельные друг другу в одной плоскости, и перпендикуляр, опущенный из начальной точки одного отрезка, проходит точно в начальную точку другого. В этом случае используйте перекрестки. Проведите еще один перпендикуляр из конечной точки первого отрезка ко второму. Если эта новая линия пересекает второй отрезок, это означает, что первый отрезок короче второго, а второй длиннее первого.
Гораздо чаще сравнивают непараллельные сегменты. В этом случае используйте компасную мерку. Разделите ноги на расстояние, равное длине одного из отрезков. Затем поставьте одну ногу на начальную точку второго отрезка. Другая нога должна находиться либо на продолжении второго сегмента, либо в нем. Этот метод используется, когда нет необходимости знать длину двух отрезков, а нужно только знать, какой отрезок короче или длиннее.
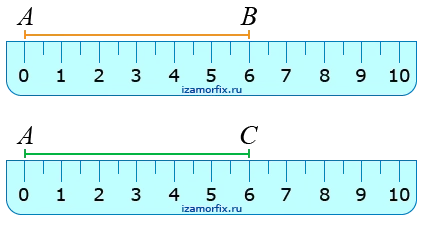
Для сравнения отрезков, не лежащих в одной плоскости, применяют метод шаблонов. Самый простой эталон — обычная школьная линейка с делениями. Но для этой цели можно использовать и другие измерительные приборы. Чтобы сравнить два отрезка, нарисованные на листе бумаги, поместите нулевое отверстие линейки на начальную точку одного из двух отрезков. Измерьте длину первой секции, а затем точно так же измерьте вторую секцию. В этом случае сначала определите численное значение длины первого сегмента, затем второго сегмента и, наконец, сравните эти значения.
Способы сравнения двух отрезков
В геометрии две фигуры, имеющие одинаковый размер и форму, считаются одинаковыми. Сравнивая цифры, вы можете выяснить, одинаковы ли они. Один из способов сделать это — наложение. Если элементы могут накладываться друг на друга, считается, что они одинаковы.
Сравнение чисел означает определение того, какое число больше или меньше. Ответ должен быть однозначным; нельзя сказать, что одна часть больше или равна другой. В математике такой ответ неверен; он не может быть приравнен ни к какому ответу.
Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; AB.
Существует множество способов сравнения чисел, выбор зависит от возможностей или обстоятельств:
- визуальный способ;
- измерительный;
- сравнение наложением;
- сравнение в координатной сетке.
Лучше всего, если они визуально отличаются по длине, чтобы можно было определить, какой из них больше, просто взглянув на них. Но это не всегда так.
Измерение длины
Самый простой способ — это измерение. Для этого можно использовать линейку. Измерив длину куска, вы узнаете, какой кусок длиннее. Если у вас нет линейки, но вы нарисовали его на квадратном листе, вы можете измерить квадраты, чтобы определить его длину. В одном сантиметре два квадрата.
Наложение друг на друга
- Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
- Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (>
Сравнение в координатной сетке
- Длина, а — Da = √((X1 — X2) ² + (Y1 — Y2) ²);
- Длина b — Db = √((X3 — X4) ² + (Y3 — Y4) ²).
√ 164>√ 73, значит, Da>








