Светлана очень хороший преподаватель, во время занятий мы сталкиваемся с множеством вопросов и обсуждаем правила русского языка на каждом примере. С удовольствием!
Определение параллельных прямых в пространстве
Прямые \(a\) и \(b\) параллельны в трехмерном пространстве только в том случае, если они лежат в одной плоскости и не пересекаются.
Если обратиться к примерам, то параллельные прямые линии можно наблюдать в виде противоположных концов прямоугольного или квадратного стола, железнодорожных путей и шпал, электрических проводов, линий в тетради на полосе и так далее. Таких примеров из реального мира можно привести множество.
Другими вариантами линий в трехмерном пространстве являются их пересечения и переходы. Пересекающиеся линии — это линии, которые имеют общую точку — точку пересечения. Пересекающиеся прямые — это те, которые лежат в разных плоскостях и не параллельны друг другу.
Существуют определенные теоремы, которые описывают поведение параллельных прямых в пространстве. Давайте рассмотрим их подробнее.
Теоремы о параллельности двух прямых
- если две прямые в пространстве перпендикулярные к одной плоскости, то они параллельные между собой;
- через точку в пространстве, что не расположена на заданной прямой, возможно провести лишь одну прямую, параллельную заданной.
Доказательство теоремы: Постройте плоскость ∝, проходящую через прямую α и точку \(M\), которая не лежит на этой прямой. Эта плоскость определяется данной прямой α и точкой \(M\), т.е. она однозначно определена.
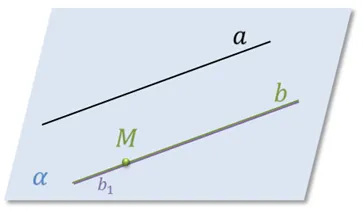
Чтобы доказать эту теорему, применим евклидову аксиому из планетометрии о параллельных прямых. Следовательно, существует только одна прямая, параллельная прямой \(a\), которая может проходить через точку \(M), и ее существование доказано. Мы называем эту линию \(b\). Два отрезка параллельны, если они лежат на параллельных прямых.
Свойства параллельных прямых в пространстве
Некоторые свойства пересекаются с вышеприведенными теоремами, но мы хотим рассмотреть их все:
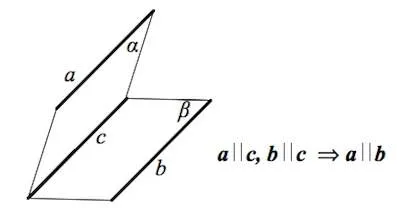
- имея две параллельных прямых, одна из которых параллельная третьей прямой, можно утверждать, что вторая тоже будет параллельна третьей;
- если из двух параллельных прямых одна пересекает некую плоскость, то и вторая так же будет ее пересекать. Это свойство является леммой про две параллельные прямые в пространстве, ее применяют при обоснованиях различных геометрических теорем;
- при помощи двух параллельных прямых можно изобразить однозначно заданную плоскость;
- через любую точку, находящуюся в 3D-пространстве и не расположенную на заданной прямой, возможно провести лишь одну прямую, что параллельна заданной.
Рассмотрим подробнее статью о параллельных прямых и докажем это. Например, прямая \(b\) пересекает плоскость \(∝\) в точке \(M\), которая лежит в некоторой плоскости. Параллельные прямые a и образуют плоскость \(b\). Поэтому если точка \(M\) является общей для плоскостей \(∝\) и \(b\), то эти плоскости пересекаются; линия пересечения обозначается c и имеет точку \(M\). Все прямые \(a\), \(b\) и \(c\) лежат в плоскости \(b\) .
Не можете найти то, что ищете?
Напишите нам, и мы поможем вам.
Аксиома планетометрии гласит, что если одна из параллельных прямых пересекает третью прямую, то вторая прямая также пересекает ее.
В нашем случае прямая a пересекает прямую c в точке \(C\) .
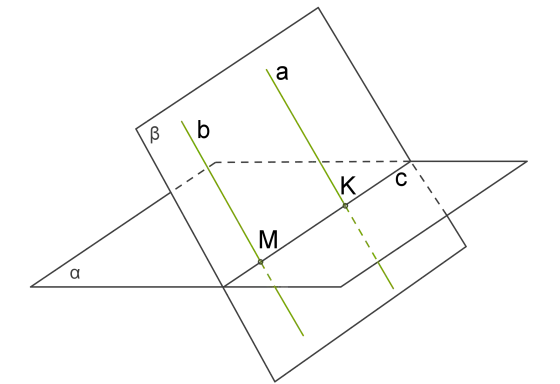
Точка \(K\) лежит одновременно на прямой α и на плоскости \(∝\), поэтому они общие. Таким образом, прямая α пересекает плоскость \(∝\) .
Параллельные прямые в пространстве
В этом уроке мы изучаем понятие параллельных прямых в пространстве. Мы дадим им определение. Мы также докажем теорему о сингулярности для прямых, параллельных данной прямой.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим обучающим видео в комплекте, вам необходимо добавить его в свой личный кабинет.
2. Распространите видеоуроки среди своих учеников в личных кабинетах.
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Параллельные прямые в пространстве»
— Изучение понятия параллельных линий в пространстве,
— Определите параллельные прямые в пространстве,
— Докажите теорему о сингулярности для прямой, параллельной данной прямой.
В планетометрии мы уже рассматривали взаимное расположение двух линий на плоскости. Напомним, что существует три возможных случая:
Первый случай. В первом случае прямые параллельны, т.е. не имеют общих точек.
Второй случай. Линии пересекаются, т.е. две линии имеют общую точку.
И третий случай. Линии совпадают, т.е. две линии имеют более одной общей точки.
Теперь обратимся к стереометрии. Помните, что стереометрия изучает свойства фигур в пространстве.
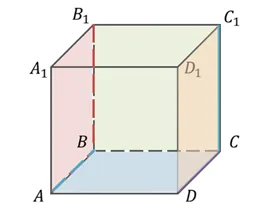
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Как вы уже знаете, параллелепипед — это пространственное твердое тело.

Линии, на которых лежат его ребра, например, A1B1, D1C1и постоянный ток параллельны. Линии, через которые проходят его диагонали, например, D1C1и DC пересекаются. Но линии на диагонали параллелепипеда A1C и край B1C1говорят, что они пересекаются.
Давайте сделаем вывод: Две линии в пространстве могут пересекаться, быть параллельными или пересекаться.
Пересекающиеся и параллельные прямые определяют плоскость. Пересекающиеся линии — это линии, через которые нельзя провести плоскость.
Давайте проанализируем случай параллельных прямых в пространстве.
Определение. Две прямые в пространстве считаются параллельными, если они лежат в одной плоскости и не пересекаются.
Обратите внимание, что фраза «если они находятся в одной плоскости» очень важна в определении. Поскольку в стереометрии мы рассматриваем трехмерное пространство, а две прямые находятся в разных плоскостях, мы не можем сказать, что они параллельны. Линии могут быть параллельными, только если они находятся в одной плоскости.
Если прямые a и b параллельны, то это выражается следующим образом.
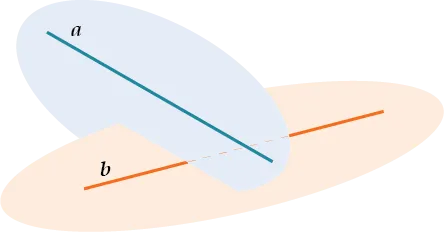
Давайте внимательно посмотрим на иллюстрацию.
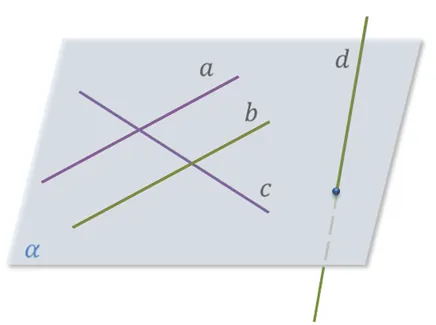
Здесь прямые a и b параллельны. Однако прямые a и c и b и d не параллельны.
Вот несколько примеров параллельных линий в пространстве.Все знакомы с железнодорожными путями.

Они видны как параллельные линии на плоской поверхности.
Внимательно просмотрите свой блокнот. Обратите внимание, что противоположные края тетради также лежат на параллельных прямых.
Прямые линии, по которым плоскость стен помещения пересекается с плоскостями потолка и пола. Они также параллельны.

Параллельность прямой и плоскости
Определение параллельности прямой и плоскости
Прямая и плоскость параллельны, если они не пересекаются, независимо от того, сколько раз они продолжаются.
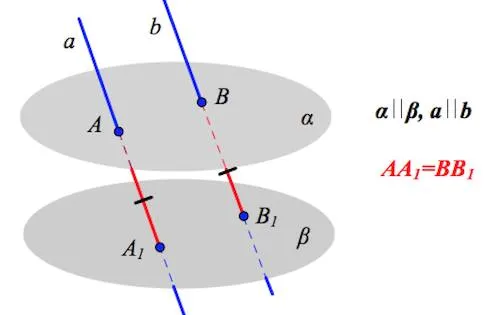
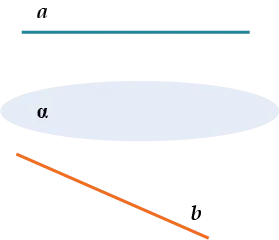
Например: Прямая линия как бы «висит» над плоскостью.
И представьте, что между прямой и плоскостью есть знак параллельности. Давайте сформулируем это так.
Признак параллельности прямой и плоскости
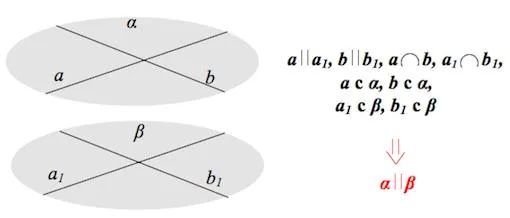
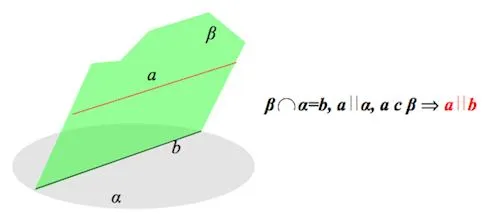
Прямая \(\displaystyle a\) параллельна плоскости \(\displaystyle \alpha\), если эта плоскость имеет (хотя бы одну!) прямую \(\displaystyle b\), параллельную \(\displaystyle a\).
Вы можете выразить его немного другими словами, но смысл останется тем же.
Если прямая \(\displaystyle a\) параллельна прямой \(\displaystyle b\), лежащей в плоскости \(\displaystyle \alpha\), то прямая \(\displaystyle a\) также параллельна всей плоскости \(\displaystyle \alpha\).
Пример на признак параллельности прямой и плоскости
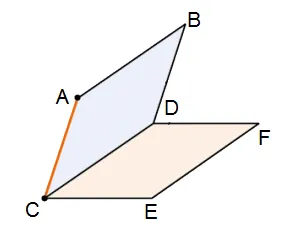
Пусть \(\displaystyle SABCD\) — правильная пирамида с 4 углами.
Тогда, например, \(\displaystyle AB\parallel SCD\). Почему? Потому что \(\displaystyle AB \parallel CD\) и \(\displaystyle CD\) лежат в плоскости \(\displaystyle SCD\).

Поэтому (по условию) \(\displaystyle AB \parallel SCD\).
Параллельность плоскостей
Определение параллельности плоскостей
Считается, что плоскости параллельны, если они не пересекаются, независимо от того, сколько раз они проходят по плоскости
И как именно
Признак параллельности двух плоскостей
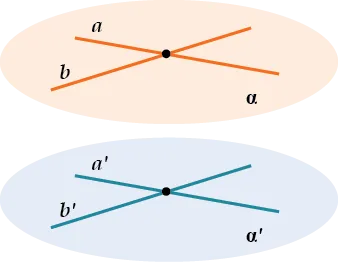
\(\displaystyle a \parallel b\) и \(\displaystyle b \parallel c
Параллельность в пространстве: свойство транзитивности
ight arrow a \parallel c\).
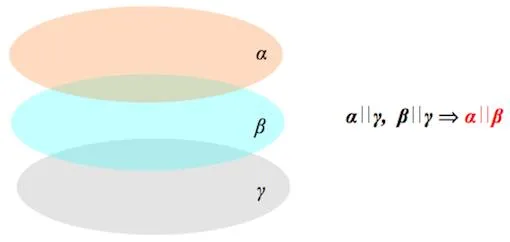
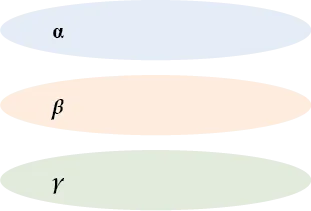
{\( \displaystyle \alpha \parallel \beta\) и \( \displaystyle \beta \parallel \gamma \Rightarrow \alpha \parallel \gamma\).
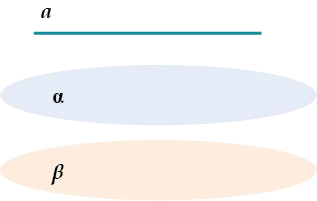
\(\displaystyle a\parallel \alpha\quad\) и \(\displaystyle \quad \alpha\parallel \beta\Rightarrow a\parallel \beta\).
\( \Displaystyle \alpha \parallel b\quad\) и \( \Displaystyle\quad b\parallel \alpha \Rightarrow text\parallel \alpha \).
И неправильное решение:
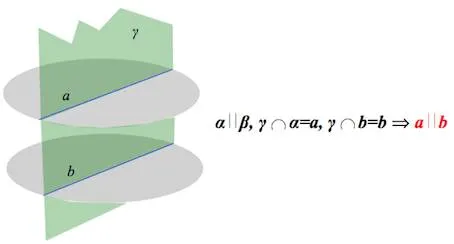
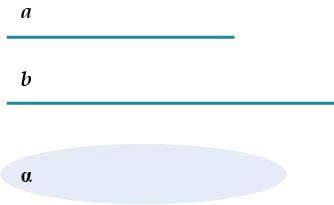
\( \displaystyle a\parallel \alpha\) и \( \displaystyle \alpha \parallel b\) \( \displaystyle NOT \Rightarrow \) \( \displaystyle a\parallel b\).
Ну, мы обсудили определения и точки параллельности прямых и плоскостей и даже немного порисовали переходные линии. Теперь давайте рассмотрим несколько примеров.
Предположим, что пирамида \( \displaystyle SABC\) имеет плоскость \( \displaystyle MNK\), проходящую через середины ребер \( \displaystyle SA\), \( \displaystyle SB\) и \( \displaystyle SC\).
Тогда \( \displaystyle MNK\parallel ABC\). Почему?
Только \( \displaystyle MN\parallel AB\) (средняя линия), \( \displaystyle NK\parallel BC\) (также средняя линия, но в \( \displaystyle \Delta SBC\)).
Получается, что \( \displaystyle MN\) и \( \displaystyle NK\) — прямые, пересекающиеся в одной плоскости, соответственно параллельны \( \displaystyle AB\) и \( \displaystyle BC\) — прямым, пересекающимся в другой плоскости — функция \( \displaystyle \Rightarrow\) \( \displaystyle MNK\parallel ABC\) работает.








