Сложение и вычитание дробей
Тест к уроку «Что такое дроби» (средний)
Тест к уроку «Простые проценты» (легкий)
Метод узлов в задаче B5
Процент: исходная величина неизвестна (метод соотношения)
Проблема B14: Переход к
Как привести дробь к общему знаменателю
Калькулятор приводит дроби к наименьшему общему знаменателю. Чтобы привести дроби к общему знаменателю, необходимо указать количество дробей и ввести дроби.
Если вы вводите вычитаемые дроби, калькулятор уменьшает дроби перед приведением их к общему знаменателю.
Нажмите кнопку Calculate, и калькулятор покажет вам, как сократить дроби до наименьшего общего знаменателя.
Приведение к общему знаменателю
Для работы с дробями часто требуется приведение дробей к общему знаменателю. Рассмотрите процесс приведения двух дробей к наименьшему общему знаменателю:
- 1 Находим наименьшее общее кратное знаменателей: НОК(8, 12)=24. Число 24 является наименьшим общим знаменателем двух дробей, приведем обе дроби к данному знаменателю. Любые две дроби можно привести к одинаковому знаменателю.
- 2 Вычисляем дополнительный множитель первой дроби .
- 3 Вычислим дополнительный множитель второй дроби .
- 4 В результате получим дроби с одинаковым знаменателем равным 24 .
Пример Приведение дробей к наименьшему общему знаменателю.

.
Примеры попыток приведения дробей к общему знаменателю.
Рассмотрим пример приведения дробей к наименьшему общему знаменателю.
Пример Сокращение дробей к наименьшему общему знаменателю.
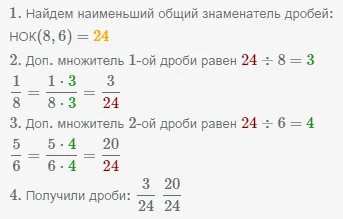
.
Рассмотрим пример сокращения нескольких дробей до наименьшего общего знаменателя нескольких дробей. Чтобы найти НОК нескольких чисел, используйте свойство: НОК(a, НОК(b, c)) = НОК(НОК(a, b), c).
Пример Назовите несколько дробей и
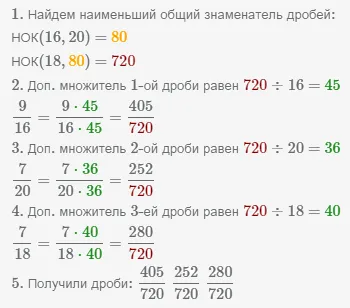
.
Общее кратное знаменателей NOC(16, 20, 18)=720.
Приведение к общему знаменателю
Первоначально я собирался включить методы приведения к общему знаменателю в раздел «Сложение и вычитание дробей». Но информации было так много, а ее важность так велика (ведь общие знаменатели — это не единственные арифметические дроби), что лучше рассмотреть эту тему отдельно.
Таким образом, у нас есть две дроби с разными знаменателями. Мы хотим, чтобы знаменатели были одинакового размера. Здесь вступает в игру основное свойство дробей, которое, напомню, заключается в следующем:
Дробь не изменяется, если ее числитель и знаменатель умножить на одно и то же ненулевое число.
Таким образом, если коэффициенты совпадают, знаменатели дробей уравниваются — этот процесс называется. А числа, которые «уравнивают» знаменатели, называются .
Почему нужно, чтобы у дробей был общий знаменатель? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Существует множество способов найти числа, при которых знаменатели дробей равны. Мы рассмотрим только три из них в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный метод, гарантирующий равенство знаменателей, — это. Мы переходим непосредственно к делу: Умножим первую дробь на знаменатель второй дроби и умножим вторую дробь
Обратите внимание, что вторая дробь ни на что не умножалась. Мы даже вдвое сократили количество расчетов!
Кстати, в этом примере я не использовал случайные дроби. Если вам интересно, попробуйте посчитать их друг против друга. После сокращения ответы будут те же, но работы будет намного больше.

В этом заключается преимущество метода общего делителя, но, опять же, его можно использовать только тогда, когда один из знаменателей делится на другой без остатка. Это довольно редкое явление.
Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).
Метод общих делителей
Как правило, дроби можно свести к наименьшему общему знаменателю. Она равна наименьшему общему кратному знаменателей дробей.
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Обратите внимание, что вторая дробь ни на что не умножалась. Мы даже вдвое сократили количество расчетов!
Решение:

Наименьшее общее кратное 4 и 6 равно 12.
\Чтобы получить знаменатель 12, умножьте числитель и знаменатель этой дроби на дополнительный коэффициент 3 (12 : 4 = 3).
\) Чтобы знаменатель дроби был равен 12, умножьте числитель и знаменатель этой дроби на дополнительный коэффициент 2 (12 : 6 = 2).
Приведение дробей к наименьшему общему знаменателю
Привести дробь к наименьшему общему знаменателю.
В сложных случаях наименьший общий знаменатель и дополнительные кратные находятся путем разложения на простые кратные.
Пример 2
Приведем к наименьшему общему знаменателю дроби \(\mathbf>\) и \(\mathbf>\)
\) к наименьшему общему знаменателю.
Решение:
Чтобы привести дробь \(\mathbf>Проанализируйте знаменатели этих дробей на простые множители:
Чтобы привести дробь \(\mathbf>\) — это произведение \(\mathbf\), то есть множители, которые нужно добавить к разложению 60, чтобы получить разложение общего знаменателя 840.
\Так же мы находим дополнительный коэффициент 5.
- Найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем
- Разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель
Пример 3
Приведение к наименьшему общему знаменателю дроби:
Приведем дроби \(\mathbf>\) и \(\mathbf>Решение:
\) к наименьшему общему знаменателю.
Приведите дроби к наименьшему общему знаменателю и сравните их:
Дополнительными множителями для дроби \(\mathbf>Решение:
Для дроби \(\mathbf>Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Старые калькуляторы могли выполнять только простые вычисления, для которых требовались простые математические операции: умножение, сложение, вычитание и деление.
\) к наименьшему общему знаменателю.
Сегодня можно использовать калькулятор для вычисления наименьшего общего знаменателя нескольких дробей и даже получить упрощенную форму с общим знаменателем.
Просто запишите дроби в такой форме: 1/2, т.е. через косую черту, поставьте
\) к наименьшему общему знаменателю.
Интересная информация

В бесплатной версии урока недоступны:
- Видео
- Изображения
- Дополнительная информация
- Таблицы
- Тесты








