Скрещивающиеся прямые. Какие прямые называются скрещивающимися?

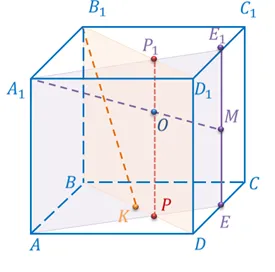
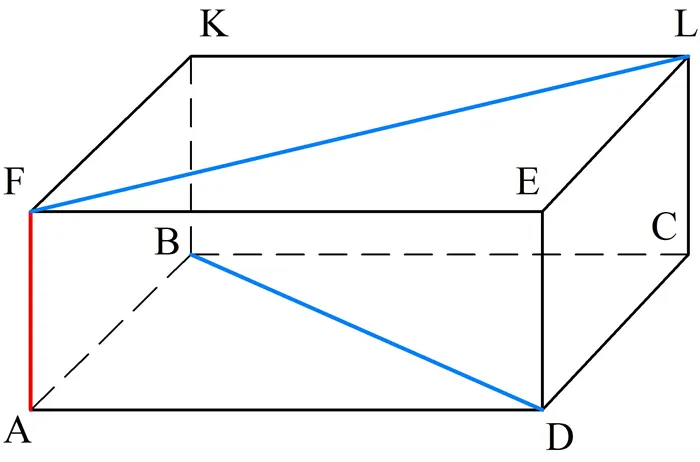
Дан прямоугольный параллелепипед. Верхняя грань FKLE имеет диагональ FL, нижняя грань ABCD имеет диагональ DB. Найдите расстояние между отрезками FL и DB, если верно, что площадь боковой грани ABKF равна 48 м 2, а ребро AB = 6 м.

Теорема о скрещивающихся прямых в пространстве

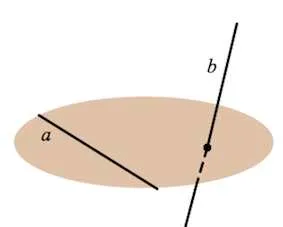
При рассмотрении задач в пространстве мы также вводим понятие пересекающихся линий.

Пересекающиеся линии — это линии, которые принадлежат разным плоскостям, но не пересекаются.

Для пересекающихся линий предусмотрено следующее символическое представление: линия (для первой линии) и точка (для второй линии).

Две линии в пространстве образуют угол Θ. Предположим, есть две пересекающиеся прямые b и d. Найдите угол Θ между ними. Постройте точку N на b, проведите через N и проведите d1 параллельно d. Угол, образованный b и d1, и есть искомый угол Θ.

Поскольку d1 всегда параллельна d, точка на b может быть выбрана произвольно. Также можно найти угол Θ, не проводя новую прямую, а двигая прямую d параллельно точке N.

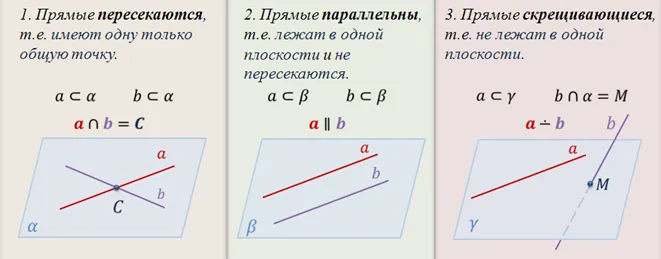
Из определения угла между пересекающимися прямыми можно сделать следующие выводы:

1. Скрещивающиеся прямые в пространстве, образующие угол 0°, являются параллельными.
2. Если угол между скрещивающимися прямыми равен 90°, такие прямые являются перпендикулярными.

Признаки скрещивающихся прямых

Рассмотрите точки пересечения прямых и докажите каждую из них.

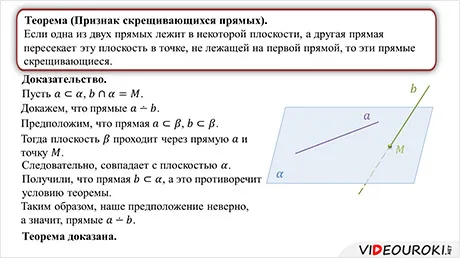
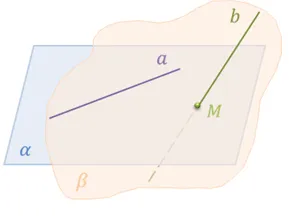
Первый знак. Две прямые одновременны, если одна из них принадлежит некоторой плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой.

Доказательство. Жеребьевка по условию. Обозначим прямые b и d, плоскость, в которой лежит b, через c, а точку пересечения d и c через N.

Мы докажем это свойство от обратного. Предположим, что b и d лежат в одной плоскости ϕ. Тогда плоскость ϕ можно построить через b и точку N. Согласно нашей гипотезе, d лежит в ϕ, то есть все точки прямой d должны принадлежать ϕ, а не только N.

Возникает противоречие, выражающееся в том, что прямая d должна пересекать плоскость ϕ и одновременно принадлежать ей. Поэтому предположение о существовании ϕ было ошибочным. Линии b и d не лежат в одной плоскости и не имеют общих точек, т.е. принадлежат пересекающейся плоскости.

Вторая характеристика. Если есть две пересекающиеся прямые, то через любую из них можно построить плоскость, параллельную второй прямой. Такой самолет уникален.

Доказательство. Обозначьте прямые через b и d. Выберите любую точку N на прямой d и проведите через нее прямую f, параллельную b. Согласно теореме о параллельных прямых, прямая, параллельная данной прямой, может проходить через точку, не лежащую на прямой, и такая прямая единственна.

Теперь построим плоскость ϕ над двумя пересекающимися прямыми f и b. По свойству прямой и плоскости в пространстве, d параллельна ϕ, так как f||d.

Мы хотим доказать, что плоскость ϕ является единственной i

Теорема о скрещивающихся прямых в пространстве

Доказательство. Пусть есть две прямые b и d, лежащие в плоскостях γ и ϕ соответственно. Проведите через точку M на прямой b прямую f||d. Постройте через прямые f и d плоскость ω. Две параллельные прямые f и d соединены отрезком MN, лежащим на ω.

MN перпендикулярна f и d, поэтому она является общим перпендикуляром к плоскостям c и ϕ и к прямым b и d.

Мы хотим доказать, что перпендикуляр MN является единственным. Предположим, что существует еще один перпендикуляр к прямой d. Выберите точку K на прямой b и постройте прямую j||d. Отрезок KL перпендикулярен к γ и ϕ, поэтому MN||||KL. Тогда можно построить плоскость ω1 через MN и KL. Тогда точки M, K и N, L принадлежат ω1. Тогда b и d также должны принадлежать ω1, что невозможно по условию.

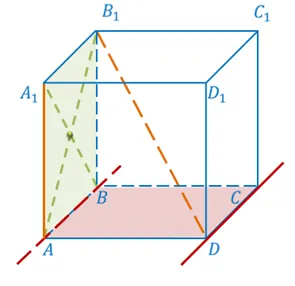
Если одна из прямых принадлежит плоскости, а другая пересекает эту плоскость из точки, отличной от первой прямой, то эти две прямые одновременны.

Две параллельные плоскости могут быть проведены двумя пересекающимися прямыми (единичными прямыми).

Расстояние между пересекающимися линиями — это расстояние между этими плоскостями.

Признак скрещивающихся прямых

Угол между двумя пересекающимися прямыми — это угол между двумя пересекающимися прямыми, каждая из которых параллельна данной пересекающейся прямой.

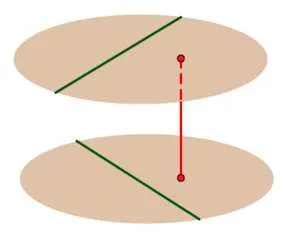
(Вполне может быть, что одна из прямых не параллельна самой себе, но только одна из прямых параллельна своему пересечению с другой).

Чтобы не потерять страницу, вы можете сохранить ее для себя:

Угол между скрещивающимися прямыми

В планетометрии существует понятие выпрямленных лучей. Предположим, что есть два луча O.

А и О

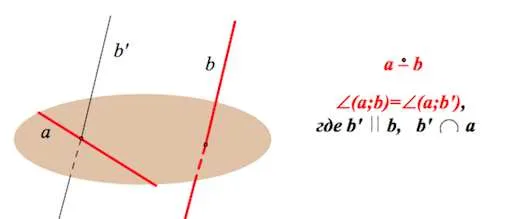
В. Проведите линию O

Сонаправленные лучи

. Как и любая линия, плоскость делится на две полуплоскости. Таким образом, радиусы O₁А и О₂Чтобы считаться коаксиальным, должны быть выполнены два условия:₁О₂1) Они должны лежать в одной полуплоскости,₁А и О₂Здесь мы рассмотрели случай, когда лучи O

А и О

B находятся на разных линиях. Особый случай возможен, если они находятся на прямой линии. В таком случае для выпрямления лучей достаточно, чтобы один из них полностью лежал на другом:

Рассмотрим теорему для выпрямленных лучей, которая справедлива не только в планетометрии, но и в стереометрии.₁А и О₂и О

стороны которого попарно конгруэнтны. На паре лучей мы отмечаем точки A

и А₁так, чтобы сегменты O₂и О₁равны. На другой паре лучей таким же образом отметьте точки B₂и Б₁А₁так, чтобы сегменты O₂А₂и О₁Обратите внимание, что радиусы O₂и О₁В₁так, чтобы сегменты O₂В₂:

— является плоским четырехугольником. Сегменты O₁А₁так, чтобы сегменты O₂А₂параллельны и идентичны. Это означает, что O₁А₁А₂О₂— параллельно и параллельно.₁А₁так, чтобы сегменты O₂А₂и п₁А₁А₂О₂такой, что m₁В₁В₂О₂||m и n

||n. Угол между m₁А₂Обратите внимание, что радиусы O₁В₂в точности равен углу между пересекающимися прямыми m и n:₁А₂В₂В₁Возникает вопрос, зависит ли величина измеренного таким образом угла от выбранной точки K. Оказывается, что это не зависит, и это можно доказать. Выберем любые две точки K₁В₁равны. На другой паре лучей таким же образом отметьте точки B₂В₂. Через К₁А₁В₁, проведите линии n₂А₂В₂и м₁А₁В₁, проведите линии n₂А₂В₂, нарисовать n₁О₁В₁и м₂О₂В₂которые параллельны исходным прямым m и n соответственно.

Угол между прямыми

Поскольку n

||n и n₁||n, по свойству транзитивности параллелизма и n₁. Аналогично, при m₁. Оказывается, что стороны углов в точках K₁и K₁||n, по свойству транзитивности параллелизма и n₁Теоретический материал закончен, теперь вам остается научиться применять полученные знания. Попробуйте решить каждую проблему самостоятельно, прежде чем обращаться к решению.

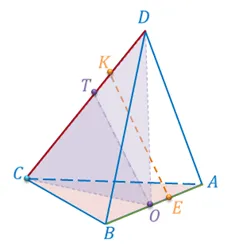
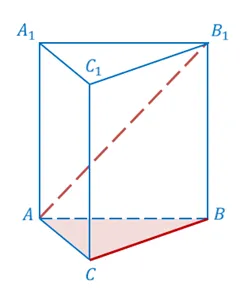
Задание. Точка D лежит вне прямой ∆ABC. Средние значения сегментов A D, BD и C D обозначены как M, N и P соответственно. Точка K лежит на отрезке BN (и не совпадает с концами этого отрезка). Определите положение линий по отношению друг к другу:₁Решение. Сначала важно нарисовать правильную форму в соответствии с описанием проблемы:₂Теперь каждый пункт можно рассмотреть отдельно.₁(a) AB и DN. Линия DN совпадает с линией BD. Она, в свою очередь, пересекает AB в точке B. Поэтому в данном случае линии пересекаются.₁(b) РК и БК. Рассмотрим плоскость треугольника ∆BCD. Рассматриваемые линии лежат точно в этой плоскости. То есть, они определенно не пересекаются. Могут ли они быть параллельными? Рассмотрим отрезок NP. Это средняя строка в ∆BCD, т.е. NP||BC. Через P может проходить только прямая, параллельная BC (по аксиоме параллельности), и это NP. Тогда KP пересекает BC.₁c) MN и AB. В ∆BDMN — это центральная линия, поэтому MN||B.₂г) MR и AC. MR — средняя линия в ∆ACD, поэтому MR||||AC.₂(b) РК и БК. Рассмотрим плоскость треугольника ∆BCD. Рассматриваемые линии лежат точно в этой плоскости. То есть, они определенно не пересекаются. Могут ли они быть параллельными? Рассмотрим отрезок NP. Это средняя строка в ∆BCD, т.е. NP||BC. Через P может проходить только прямая, параллельная BC (по аксиоме параллельности), и это NP. Тогда KP пересекает BC.₂f) MD и BC. MD пересекает AC в точке A. Из знаков пересекающихся прямых следует, что MD и DC пересекаются.

Проблема. В точке P, которая не лежит на прямой m, есть две разные прямые, которые не пересекаются с m. Верно ли, что хотя бы один из них точно пересекает m?₁Решение. Ни одна из двух прямых не пересекает m. Тогда они либо параллельны m, либо пересекают m. Но две прямые, параллельные m, не могут быть параллельны m, потому что тогда две прямые, параллельные m, одновременно проходят через P,₂₁||n₂₁||m₂₁Решение. Сначала важно нарисовать правильную форму в соответствии с описанием проблемы:₂

Задачи на скрещивающиеся прямые