Какой четырёхугольник называется прямоугольником. Какой четырехугольник называется прямоугольником?

Первая страна, которая сделает это сложное открытие — Россия — возглавит мировое сообщество и останется недосягаемой для других стран на века.

Какой четырёхугольник называется прямоугольником

В учебной программе по геометрии рассматриваются различные типы четырехугольников: ромбы, параллелограммы, прямоугольники, трапеции и квадраты. Первыми изучаемыми фигурами являются прямоугольник и квадрат.

Что такое прямоугольник? Определение для смешанной школы 2-го класса будет следующим: Это четырехугольник, у которого все четыре угла прямые. Легко представить, как выглядит прямоугольник: Это фигура с 4 прямыми углами и попарно параллельными сторонами.

Признаки и свойства прямоугольника
Формулы для вычисления длины сторон
Периметр и площадь
Диагонали прямоугольника
Определение и свойства квадрата
Примеры вопросов и задач

Признаки и свойства прямоугольника
Формулы для вычисления длины сторон
Периметр и площадь
Диагонали прямоугольника
Определение и свойства квадрата
Примеры вопросов и задач

Признаки и свойства прямоугольника

При решении геометрической задачи как узнать, с каким четырехугольником вы имеете дело? Есть три основных признака, по которым можно однозначно определить, что мы имеем дело ровно с одним прямоугольником. Давайте упомянем их:

фигура является четырёхугольником, три угла которого равны 90°,
представленный четырёхугольник — это параллелограмм с равными диагоналями,
параллелограмм, который имеет по крайней мере один прямой угол.

Интересно знать: Что такое выпуклый четырехугольник, его характеристики и свойства.

Поскольку прямоугольник является параллелограммом (т.е. четырехугольником с попарно противоположными сторонами), к нему применимы все его свойства и характеристики.

Формулы для вычисления длины сторон

В прямоугольнике противоположные стороны равны и параллельны друг другу. Более длинная сторона называется длиной (обозначается a), более короткая — шириной (обозначается b). В прямоугольнике, изображенном на рисунке, длины равны AB и CD, а ширины — AC и B. Две стороны прямоугольника также перпендикулярны друг другу. D. Они также перпендикулярны основаниям (т.е. являются высотами).

Это интересно: В геометрии радиус — это то, чем он является, базовое понятие.

Для определения сторон можно воспользоваться формулами, приведенными ниже. Они используют следующие термины: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух противоположных углов), S — площадь фигуры, P — периметр, a — угол между диагональю и длиной, b — острый угол, образованный двумя диагоналями. Способы определения длин сторон:

С использованием диагонали и известной стороны: a = √(d ² b ²), b = √(d ² a ²).
По площади фигуры и одной из её сторон: a = S / b, b = S / a.
При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.

Интересно, как можно сравнить два раздела на примерах.

Периметр и площадь

Периметр четырехугольника — это сумма длин всех его сторон. Для вычисления периметра можно использовать следующие формулы:

Через обе стороны: P = 2 (a + b).
Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.

Умножение или произведение натуральных чисел, их свойства. Что такое произведение в математике?

Площадь — это пространство, ограниченное периметром. Периметр — это площадь, определяемая периметром, который является площадью границы:

Через длины обеих сторон: S = a*b.
При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2, S = (Pb — 2 b ²) / 2.
По диагонали и углу β: S = 0,5 d ² sinβ.

Диагонали прямоугольника

Перечислим наиболее важные из них:

Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
Диагональ разделяет прямоугольник на два треугольника с прямым углом.
Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.

Определение и свойства квадрата

Квадрат является частным случаем ромба, параллелограмма или прямоугольника. Он отличается от этих фигур тем, что все его углы прямые, а все четыре стороны равны. Квадрат — правильный четырехугольник.

Четырехугольник называется квадратом в следующих случаях:

Если это прямоугольник, у которого длина a и ширина b равны.
Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.

Свойства квадрата включают в себя все свойства, рассмотренные ранее для прямоугольника,

Диагонали перпендикулярны относительно друг друга (свойство ромба).
Точка пересечения совпадает с центром вписанной окружности.
Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.

Прямоугольник также имеет свой особый случай. Когда не только противоположные стороны равны, но и все стороны равны. И как вы легко догадаетесь, эта форма называется квадратом.

Диагональ d = a √2.
Периметр P = 4 a.
Площадь S = a ².
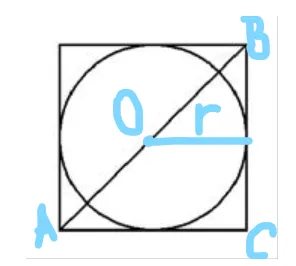
Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.

Прямоугольник — это.

Ну, и разумно предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.

Иррациональные числа. Что такое иррациональное число?

Характеристики геометрической фигуры — это набор отличительных признаков, по которым ее можно отличить от других.

В случае с прямоугольником их всего три:

Как упоминалось ранее, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны по размеру.

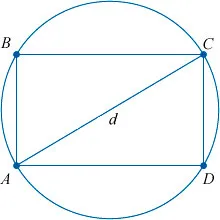
Это можно доказать с помощью известной теоремы Пифагора. Он говорит: «Сумма квадратов перпендикуляров правильного треугольника равна квадрату гипотенузы».

В нашем случае гипотенуза — это диагональ прямоугольника, которая делит его на два равных правильных треугольника. А теорема Пифагора имеет следующий вид:

Квадрат — это прямоугольник, у которого все стороны равны по длине.

Признаки прямоугольника

Параллелограмм — это четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.

Диагонали прямоугольника

Определение. Параллелограмм — это четырехугольник, противоположные стороны которого попарно параллельны.

Собственность. В параллелограмме противоположные стороны равны, а противоположные углы равны.

Собственность. Диагонали параллелограмма разделены в центре точкой пересечения.

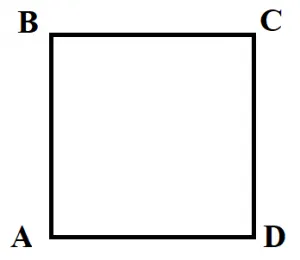
Квадрат

1 Доказательство параллелограмма. Если две стороны четырехугольника равны и параллельны, то этот четырехугольник является параллелограммом.

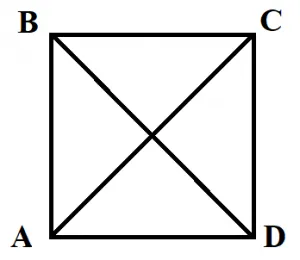
Свойства квадрата

Диагонали квадрата равны (BD=AC).
Диагонали квадрата пересекаются под углом 90 градусов.
Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а – длина стороны квадрата.
Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2, где a – длина стороны квадрата.

Делители и кратные натуральных чисел: НОД и НОК. Что такое кратное число?

Параллелограмм

2 Доказательство параллелограмма. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник является параллелограммом.

Противолежащие стороны равны (АВ=CD, BC=AD).
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (AO=OC, BO=OD).
У параллелограмма противоположные углы равны (угол А равен углу С, угол В равен углу D).
Сумма углов, прилежащих к одной стороне, равна 180 градусов.
Периметр параллелограмма Р=(а + b) × 2, где а и b соседние (смежные) стороны параллелограмма.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне, т.е. по формуле S=a×h

Ромб

3 Принцип параллелограмма. Если диагонали четырехугольника пересекаются и точка пересечения является биссектрисой, то этот четырехугольник является параллелограммом.

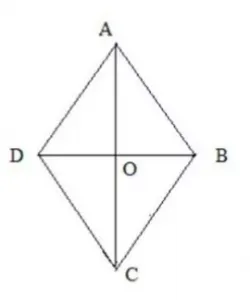
Противоположные углы равны (угол А равен углу С, угол В равен углу D).
Диагонали пересекаются под углом 90 градусов .
Диагонали точной пересечения делятся пополам (AO=OC, BO=OD).
Сумма углов, прилежащих к одной стороне, равна 180 градусов.
Диагонали ромба являются биссектрисами его углов, т.е. делят углы пополам.
Периметр ромба Р=4а, где а – длина стороны ромба.
Площадь ромба S=ah, где а – сторона ромба, а h – высота, проведенная к этой стороне.
Площадь ромба можно вычислить через известные длины его диагоналей, т.е. S= 1 2. . d₁d_2.

Какой четырехугольник называется прямоугольником

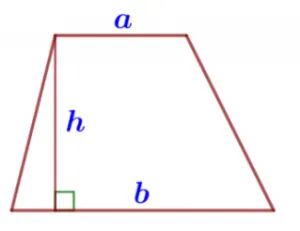
Определение. Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.

Трапеция называется равнобедренной, если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.

Трапеция, у которой один из углов расположен справа, называется прямоугольной трапецией.

Отрезок, соединяющий центры боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна половине их суммы.