На рисунке 2 показана полилиния \( \small A_1A_2A_3A_4A_5A_6). Эта полилиния является вырожденной, потому что отрезки \( \малый A_2A_3) и \( \малый A_3A_4) лежат на одной прямой.
Ломаная линия
Полилиния — это геометрическая фигура, состоящая из последовательно соединенных сегментов, где конец одного сегмента является началом следующего. Однако смежные отрезки (с общей точкой) не обязательно лежат на одной прямой.
Отрезки, составляющие полилинию, называются соединениями, а концы этих отрезков — вершинами полилинии.
Построим полилинию с четырьмя сегментами:
Отрезки AB, BC, CD и DE — это отрезки полилинии. Точки A, B, C, D и E являются вершинами полилинии, которую вы формируете, добавляя буквы к вершинам в правильном порядке. Например, скажите или напишите: polyline ABCDE или polyline EDCBA .
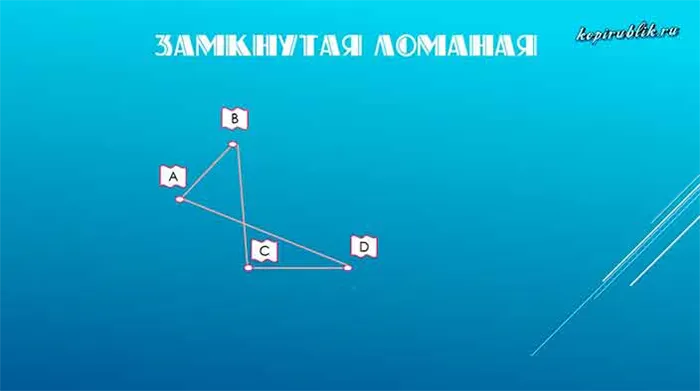
Самопересекающаяся ломаная
Закрытая и открытая полилинии могут быть самостоятельными. Самопересекающаяся полилиния — это полилиния, соединения которой пересекаются в одной или нескольких точках. Например:
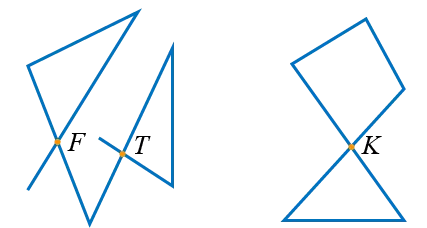
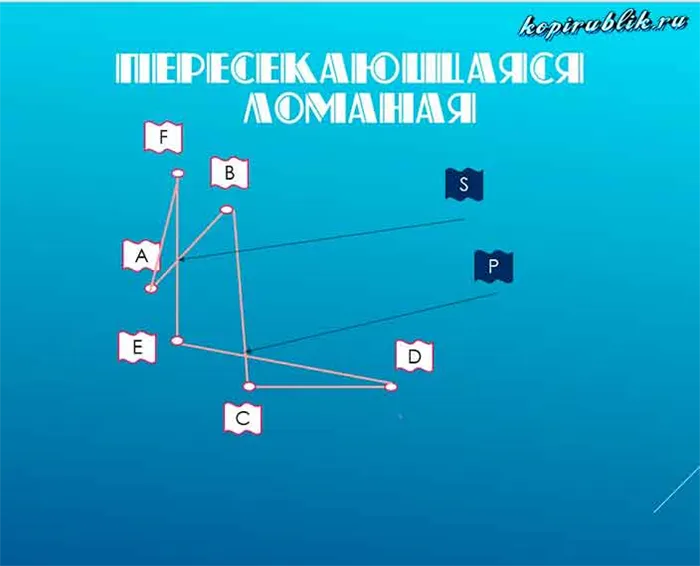
точки F, T, K являются самозаканчивающимися точками, то есть точками, в которых полилиния пересекает саму себя.
Длина ломаной
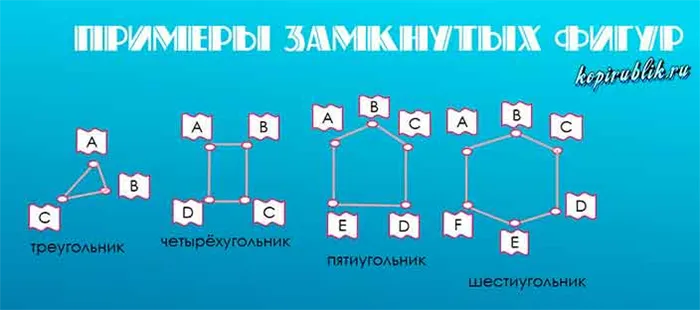
Длина полилинии — это сумма длин всех ее сегментов. Длина замкнутой полилинии без независимых пересечений, т.е. длина многоугольника, называется периметром.
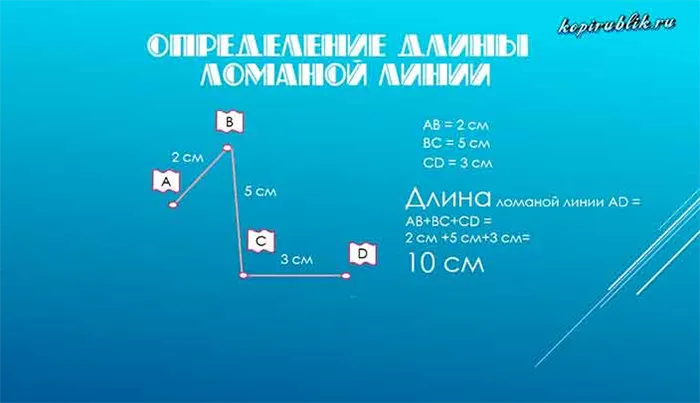
Пример 1: Определите длину трехсегментной полилинии.
Решение. Длина полилинии ABCD равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина полилинии ABCD равна 9 см.
Пример 2: Найти длину замкнутой полилинии.
Решение: Найдите окружность замкнутой полилинии, сложив длины всех отрезков:
AB + BC + CD + DA = 3 см + 5 см + 5 см + 4 см + 5 см = 17 см.
Ответ: 17 см.
Звенья, вершины и длина
Чтобы полностью понять природу и свойства этого понятия, следует рассмотреть, что такое связи полилинии в математике и что такое ее вершины и длины:

- Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
- Точки соединения концов этих отрезков называются вершинами.
- Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
- Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
- Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.
Интересно знать: Что такое выпуклый четырехугольник, его характеристики и свойства.
Его название состоит из латинских заглавных букв, написанных на вершинах:
- Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
- Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).
Как правило, такой набор называется ABCDE или EDCBA.
Примечание: Что такое радиус в геометрии.
Разновидности
В геометрии принято выделять несколько разновидностей на основе их структуры:
- Замкнутые самопересекающиеся.
- Незамкнутые самопересекающиеся.
- Замкнутые без самопересечений.
- Незамкнутые без самопересечений.
Как описано выше, замкнутая, не перекрывающаяся форма называется многоугольником.
Читайте также.
Когда члены фигуры пересекаются друг с другом, фигура называется самопересекающейся.
Многоугольники
Многоугольник — это геометрическая фигура, характеризующаяся количеством углов и связей. Углы образуются парами звеньев замкнутой полилинии, которые сходятся в одной точке. Ссылка
Точки представляют собой вершины треугольника, а отрезки — его стороны. Возле каждой угловой точки образуется угол треугольника. Таким образом, эта форма имеет три угла, что и дает ей название.
Различают следующие типы треугольников:
Свойства
Плоская геометрическая фигура с четырьмя углами и четырьмя сторонами называется четырехугольником.
- Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
- Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
- Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
- Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости. Выиграть в российских казино может каждый. Вероятность получения выигрыша с азартных игр зависит только от удачливости игрока. Чтобы увеличить шансы на победу, стоит выбирать слоты с высоким уровнем RTP и различными бонусными опциями. Если же в слоте есть джекпот, шансы на крупный денежный приз увеличиваются в несколько раз.
- Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
- Если все стороны и углы многоугольника равны, он называется правильным.
Треугольники
Читайте также: Клеточное строение листа (схема) Функции и свойства клеток.
Если все углы четырехугольника направлены вправо, то это прямоугольник.
Правильный четырехугольник называется квадратом.
- Равносторонние — все стороны их равны по длине.
- Разносторонние — все стороны различаются по длине.
- Равнобедренные — две стороны из трех имеют одинаковую длину.
- Остроугольные — если все углы острые.
- Прямоугольные — если имеется прямой угол.
- Тупоугольные — если есть один тупой угол.
Четырехугольники
Существуют и другие виды четырехугольников: ромбы, трапеции, параллелограммы и т.д. Все они следуют общим правилам, описанным выше.
Классификация пунктирных линий сначала основана на свойстве замкнутости.
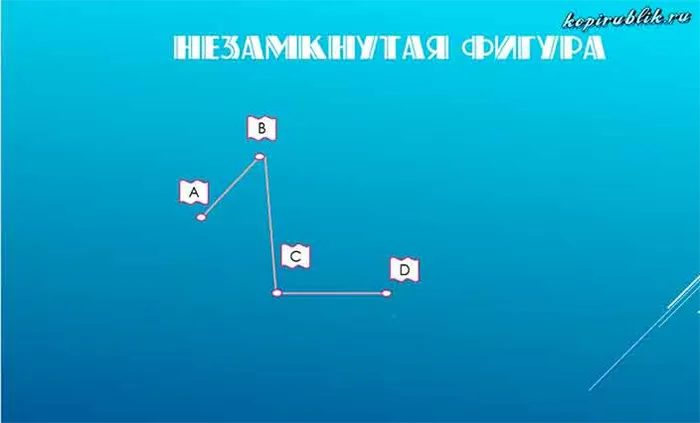
Замкнутая линия — это фигура, конечное положение которой совпадает с ее начальным положением. Другими словами, если она заканчивается в той же точке, где началась.
Яркими представителями являются треугольник и квадрат, а также другие виды многоугольников:
Незамкнутая пунктирная линия — это фигура, занимающая позицию, отличную от начальной.
Признак замкнутости ломаной линии
Иногда студентам задают вопрос: «Как определить, замкнута фигура или нет?». Ответ очень прост: «Если число отрезков равно числу вершин, то он замкнут, но если наблюдается неравенство, то он открыт».
В качестве дополнительной формулы можно рассмотреть понятие самопересекающейся линии — линии, которая пересекает сама себя на своем пути. Для этой концепции не имеет значения, сколько раз происходило пересечение.
Пересечения S, P и вершины A, B, C, D, E, F отмечены на рисунке.
Иногда люди спрашивают: «Могут ли вершины быть пересечениями?». Чтобы найти ответ, посмотрите на рисунок пересеченной и в то же время замкнутой — пунктирной линии:
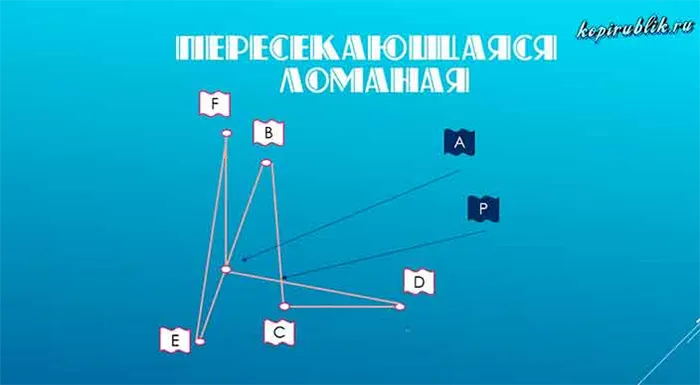
Изображение отличается от предыдущего: Отрезок EB сместился так, что вершина A приобрела свойство пересечения.
Отрезок линии с началом и концом имеет общую формальную характеристику — длину. Если вы хотите измерить его длину, вам нужно сложить длины всех его составляющих — отрезков.
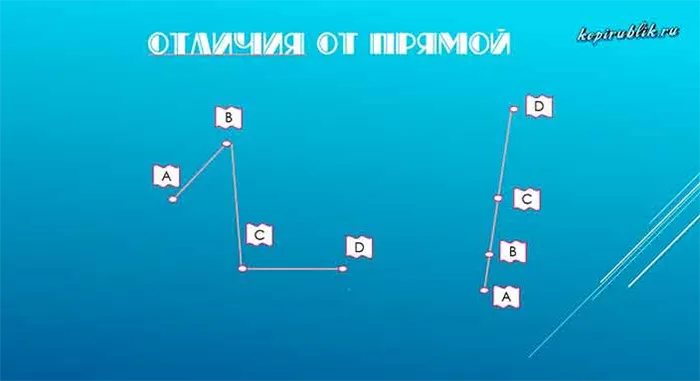
Взглянув на иллюстрацию, становится ясно: единственная характеристика пунктирной линии — отсутствие углов, соответствующих 180 градусам. В остальном формы одинаковы и имеют схожие характеристики, например, длину.
Как измерить длину ломаной линии
Чем ломаная линия отличается от прямой