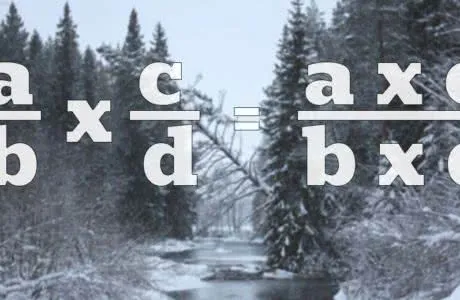Когда мы приводим дроби к общему знаменателю, мы, по сути, пытаемся найти число, которое делится на каждый из знаменателей. Затем знаменатели двух дробей уменьшаются до этого числа.
Общий знаменатель алгебраических дробей
Например, для \(\frac\) и \(\frac\) общим знаменателем является \(5ab\), потому что это выражение содержит все коэффициенты первого знаменателя (т.е. пять и \(a\)) и все коэффициенты второго (т.е. \(b\)).
Значит, чтобы найти общий знаменатель, нужно просто перемножить знаменатели всех дробей? В целом, да. На практике, однако, этот метод часто оказывается непрактичным, поскольку приводит к громоздким вычислениям в дальнейшем. По этой причине принято находить наименьший общий знаменатель.
Например, в случае с дробями \(\frac\) и \(\frac\), наименьшим общим знаменателем является \(abc\), но не \(a^2 b^2c\) (который вы получите простым умножением \(ab\) и \(abc\)).
Как искать наименьший общий знаменатель?
В приведенном выше примере наименьший общий знаменатель был очевиден. Однако в более сложных случаях это не так просто понять.
Пример. Найдите общий знаменатель для дробей \(\frac\) и \(\frac\).

Пример. Найдите общий знаменатель дробей \(\frac\), \(\frac\) и \(\frac\) .
Решение. Снова перемножим знаменатели всех трех дробей, а затем соберем нашего Франкенштейна:

Пример общего знаменателя :
Чтобы понять, «что такое общий знаменатель», нам нужен пример двух дробей и одной энергии (иначе это не имеет смысла), скажем, две дроби 1/2 и 1/3 и энергия сложения — «+».
Для малых чисел, таких как 2 и 3, «нокс» равен 6. Нам не нужен инструмент для этого, вы, вероятно, тоже вычислили это в своей голове.
То есть, 6 делится на 2 без остатка 6 : 2 = 3 и 6 делится на 3 без остатка 6 : 3 = 2.
У нас есть два числа, первую дробь 1/2 нужно умножить на 3, чтобы получить общий знаменатель 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы также получить общий знаменатель 6: 1*2/3*2 = 2/6.
Найдя общий знаменатель, мы можем выполнить операцию, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Найдя «общий знаменатель», мы можем выполнить требуемую операцию с дробями.
1 2 + 1 3 = 1*3 2*3 + 1*2 3*2 = 3 6 + 2 6 = 3 + 2 6 = 5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный вопрос для поиска: «В каком случае числа двух дробей являются произведением знаменателей?». «, который не приведен выше.
По крайней мере, когда знаменатели являются простыми числами, то есть, например, в случае вышеупомянутых дробей со знаменателями 2 и 3. Эти числа являются простыми числами, то есть они кратны самим себе и 1.
А общим знаменателем двух чисел 2 и 3 будет произведение 2 * 3 = 6.
Пример нахождения общего знаменателя методом разложения на множители
Это то же самое, что и «NOC» выше — только может называться по-другому.
Этот метод также можно назвать «нахождение общего знаменателя с помощью факторизации».
Или «метод S
Подумайте над следующим примером: найдите наименьший общий знаменатель дроби \(\frac, \frac, \frac\).
Решение: Мы хотим разложить знаменатели чисел 11, 15 и 22 на простые множители.
Число 11 само по себе является простым числом, поэтому нет необходимости его разлагать. Разложить 15=5⋅3 Разложить 22=11⋅2
Найдите наименьшее общее кратное (НОК) знаменателей 11, 15 и 22. НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для этих дробей. Теперь приведите данные дроби \(\frac, \frac, \frac\) к общему знаменателю 330.
Правила или алгоритм приведения дробей к общему знаменателю.
Какой общий знаменатель у дробей \(\frac) и \(frac)? Ответ: Какой наименьший общий знаменатель у 14 и 25? Мы используем алгоритм приведения дробей к общему знаменателю алгебраических дробей.
- Нужно разложить на простые множители знаменатели дробей.
- Нужно найти наименьшее общее кратное (НОК) для знаменателей данных дробей.
- Привести дроби к общему знаменателю, то есть умножить и числитель и знаменатель дроби на множитель.
Общий знаменатель для нескольких дробей.
Сначала разложим знаменатели 14 и 25 на простые множители. 14=2⋅7 25=5⋅5 Теперь найдем NOC(14,25)=2⋅7⋅5⋅5⋅5⋅5=350.
То, что мы нашли, является наименьшим общим знаменателем:
Но не всегда необходимо находить наименьший общий знаменатель, иногда можно найти любой знаменатель и затем сократить конечную дробь. Например, в случае с дробями \(\frac\) и \(\frac\) знаменатель может быть 700, 1400 и т.д.
Отменить ответ
Вы должны войти в систему, чтобы оставить комментарий.
Пожалуйста, отключите блокировщики рекламы или добавьте этот сайт в исключения блокировщиков рекламы, если вы хотите, чтобы этот проект продолжался.
Правило поиска OZ и NOZ также применяется к нескольким фракциям подряд. Есть три значения: 3/9, 8/11 и 10/12. Чтобы перевести их, выполните те же действия, что и в правиле:
NOQ (9, 11) = 99, NOQ (99, 12) = 39, NOQ (9, 11, 12) = 396,
396/9 = 44; 396/11 = 36; 396/12 = 33;
3*44/9*44 = 132/396; 8*36/11*36 =288/396; 10*33/12*33 =330/396;
You may also like:

Что такое уравнение и корни уравнения? Как решить уравнение?

Деление рациональных чисел примеры и правила.

Нужен репетитор по математике (алгебре) или геометрии?