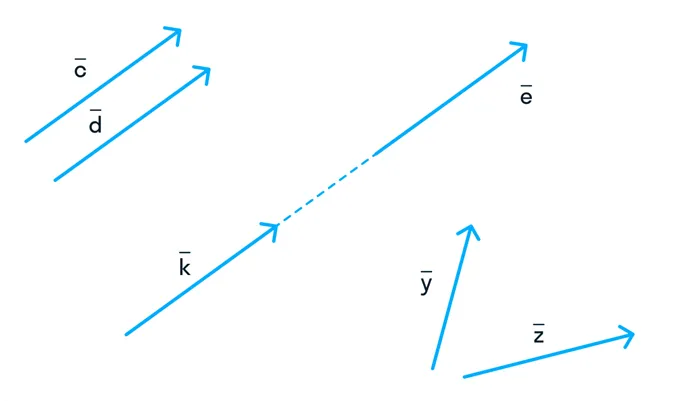
Решение. Во всех случаях мы будем просто перемещать векторы в начало координат и брать радиус вектора. Тогда мы просто посмотрим на координаты конца радиус-вектора. Мы начинаем с :
Векторы: основные понятия. Координаты вектора. Длина вектора
Тот факт, что вектор — это направленный отрезок, будет легче понять, если мы рассмотрим различия между скалярными и векторными величинами.
В таблице ниже «не-векторы» — это скалярные величины или просто скалярные величины, а «векторы» — векторные величины.
| Невекторы | Организации |
| Масса | Гравитация |
| Длина | Путь |
| Время | Ускорение |
| Плотность | Давление |
| Температура | Скорость |
| Группа | |
| Регион | |
| Векторная единица |
Векторы (скаляры) не имеют направления, а векторы имеют направление.
Вектор обязательно проходит из точки A по прямой в точку B. Численное значение вектора — это длина, а физическое и геометрическое значение — направление. Отсюда следует первое, более простое определение вектора. Таким образом, вектор — это направленный отрезок, ведущий из точки A в точку B и обозначаемый через .
И чтобы начать различные операции с векторами, нам необходимо ознакомиться с еще одним определением вектора.
Вектор — это способ представления точки, которую можно достичь из определенной начальной точки. Например, трехмерный вектор обычно записывается в виде ( x, y, z ). Проще говоря, эти цифры показывают, какое расстояние нужно проехать в трех разных направлениях, чтобы достичь точки.
Давайте зададим вектор. В данном случае x = 3 (правая рука указывает вправо), y = 1 (левая рука указывает вперед), z = 5 (под точкой находится лестница, ведущая вверх). Согласно этому, вы находите точку, пройдя 3 метра в направлении, на которое указывает правая рука, затем 1 метр в направлении, на которое указывает левая рука, а затем вас ждет лестница, и если вы подниметесь на 5 метров, то, наконец, достигнете конечной точки.
Все остальные термины являются уточнениями вышеприведенного объяснения, которые необходимы для различных операций с векторами, то есть для решения практических задач. Давайте рассмотрим эти более строгие определения, остановившись на формальных векторных задачах.
Физическими примерами векторных величин являются смещение материальной точки, перемещающейся в пространстве, скорость и ускорение этой точки и сила, действующая на нее.
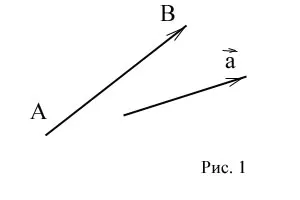
Геометрический вектор представлен в двух- и трехмерном пространстве в виде направленного отрезка. Это раздел с началом и концом.
Если A — начало, а B — конец вектора, то вектор обозначается символом или простой строчной буквой. На рисунке конец вектора обозначается стрелкой (рис. 1).
Длина (или единица) геометрического вектора — это длина отрезка, который его создает.
Два вектора считаются равными, если они могут быть выровнены.
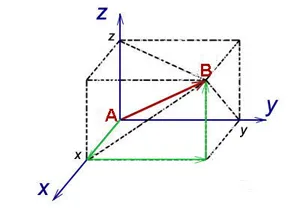
С любой точкой M в пространстве мы связываем вектор
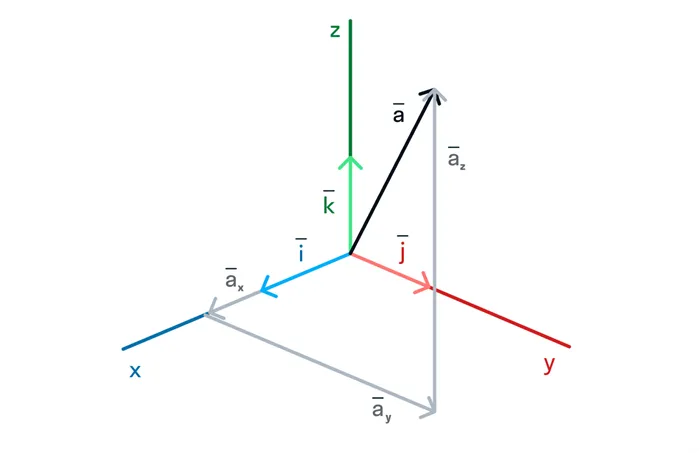
Координаты вектора в прямоугольной декартовой системой координат в пространстве
строительный вектор a точки M и спроецировать его на каждую из координатных осей. Обозначим значения соответствующих проекций:
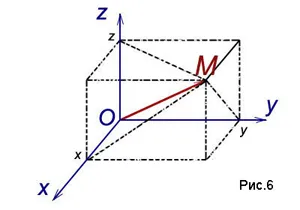
Числа x, y, z называются координатами точки M, то есть абсциссой, ординатой и аппликатой, и записываются как упорядоченные точечные числа: M (x; y; z) (рис. 6).
Вектор единичной длины, направление которого совпадает с направлением оси, называется единичным вектором (или ортогональным вектором) оси. Обозначим через
Аналогично, порядки координатных осей: Ox, Oy, Oz
Теорема. Каждый вектор может быть проанализирован в терминах координатных осей:
Уравнение (2) называется разложением вектора по координатным осям. Коэффициенты этого разложения являются проекциями вектора на координатные оси. Поэтому коэффициенты разложения (2) вектора по координатным осям являются координатами вектора.
Поскольку вектор и тройка его координат однозначно определены в пространстве, вектор можно записать в следующей форме.
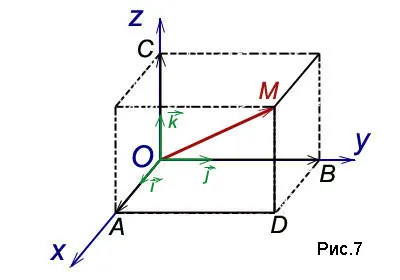
Векторные представления формы (2) и (3) идентичны.
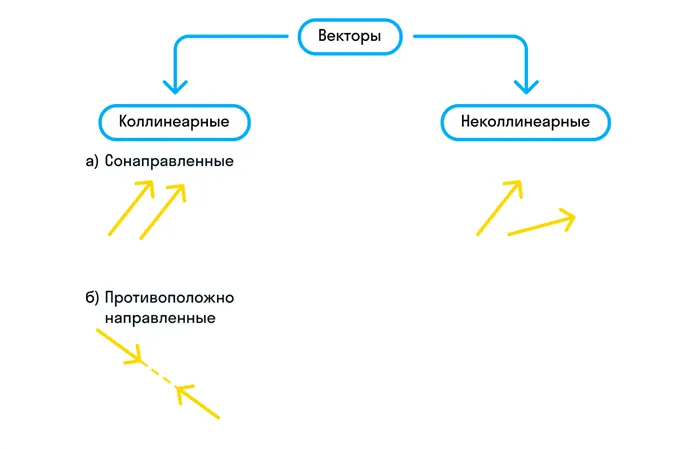
Векторы считаются коллинеарными, если они связаны следующим соотношением.
Пусть векторы будут. Эти векторы коллинеарны, если координаты векторов связаны друг с другом следующим образом.
Условие коллинеарности векторов в координатах
То есть координаты векторов пропорциональны.
Пример 1. Коллинеарны ли эти векторы?
Решение. Найдите отношение координат данных векторов:
Координаты векторов пропорциональны, то есть векторы коллинеарны или, что одно и то же, параллельны.
Векторы
i → и j →
Координатные векторы
называются координатными векторами для данной системы координат.Мы выводим любой вектор a → из начала координат. Согласно геометрическому определению операций над векторами, вектор a → можно представить в виде a → = a x — i → + a y — j →, где коэффициентами являютсяи
— уникальны, их уникальность можно легко доказать обратным методом.a xРазложение вектораa ya →
Разложение вектора
с векторами координатi → и j →в плоскостиМы выводим любой вектор a → из начала координат. Согласно геометрическому определению операций над векторами, вектор a → можно представить в виде a → = a x — i → + a y — j →, где коэффициентами являютсяКоэффициенты a x и a yназываются координатами вектора в соответствующей системе координат на плоскости.
Принято записывать координаты вектора в этой системе координат в скобках через запятую, при этом указанные координаты отделяются от векторного обозначения знаком равенства. Например, обозначение a → = ( 2 ; — 3 ) означает, что вектор a → в данной системе координат имеет координаты ( 2 ; — 3 ) и может быть представлен как продолжение координатных векторов i → и j → в виде a → = 2 — i → — 3 — j →.Обратите внимание, что порядок записи координат важен
Для прямоугольной системы координат в трехмерном пространстве все точки, упомянутые выше, могут быть определены аналогичным образом. В этой системе координат есть три координатных вектора i →, j →, k →, и любой вектор a → расширяется не по двум, а по трем координатам и имеет вид a → = a x — i → + a y — j → + a z — k →, а коэффициенты этого расширения ( a x ; a y ; a z ) называются
координаты вектора в заданной (трехмерной) системе координат.
Поэтому векторы координат в трехмерном пространстве также принимают значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ; 0 ), j → = ( 0 ; 1 ; 0 ), k → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0, 0, 0 ), и в этом случае два вектора считаются равными, если все три соответствующие координаты вектора между ними равны a → = b → ⇔ a x = b x, a y = b y, a z = b z, а координаты противоположного вектора a → противоположны соответствующим координатам вектора a →, т.е. т.е. — a → = ( — a x ; — a y ; — a z ) .
Из уроков алгебры мы знаем прямоугольную систему координат. Она имеет оси O и O, и каждая точка, отмеченная на плоскости, имеет свои координаты:
Равные и противоположные векторы
Конечно, мы также можем отмечать векторы в координатной плоскости. Построим два вектора, которые начинаются в начале координат, имеют длину 1 и направления которых соответствуют направлениям координатных осей. Вектор на оси О обозначается i, а вектор на оси О — j.Эти векторы называются единичными векторами или ортонами (также используется термин координатный вектор). Они неколлинеарны, что означает, что любой вектор на плоскости может быть разложен на единичные векторы. Коэффициенты такого разложения — это просто координаты вектора.
Давайте на примере найдем координаты вектора. Предположим, у нас есть вектор a :Нам нужно разложить a на векторы i и j. Для этого нам нужно посмотреть на него с определенной точки. Удобно переместить вектор a в начало координат:
Теперь нужно провести прямые, параллельные векторам i и j через конец a. В результате получится прямоугольник ABCD:
Мы можем записать равенство:Поэтому координатами этого вектора являются числа 3 и 2. Он записывается следующим образом:
Обратите внимание, что порядок цифр в скобках имеет существенное значение. Первое число — это коэффициент разложения перед вектором i. Эту координату можно назвать координатой x (по аналогии с координатами точки). Второе число — это коэффициент вектора j, который является координатой y. Отметим также очевидный факт, что координаты равных векторов одинаковы.
Координаты векторов
На сайте

Это обозначение означает, что c имеет координаты 1
. Поэтому мы можем сформулировать правило сложения векторов:
Поясним это правило на примере. Добавим векторы a и b. Понятно, что результатом будет новый вектор, который мы обозначим через c. Чтобы найти его первую координату, сложим первые координаты векторов a и b :
Чтобы найти его вторую координату, мы складываем вторые координаты соответствующих векторов:

В результате получается вектор с .
Задача. Добавьте векторы, имеющие координаты:

Решение. Сначала просто сложите простые числа в скобках (и получите координату x ), затем сложите вторые числа (и получите координату y ):
Теперь давайте попробуем понять, как вычисляется разница между двумя векторами. Предположим, что у нас есть векторы с заданными координатами a 1
и b 2

. Давайте снова запишем их эволюцию в единичных векторах:

Теперь мы можем сформулировать правило для вычитания векторов:
Сложение и вычитание векторов
Например, вычтем вектор b из вектора a. Искомая разность — это вектор, координата x которого равна разности простых координат векторов a и b:; у1>Аналогично вычисляем координату y:; у2>В результате мы имеем вектор с координатами .

Задача. Вычтите вектор b из вектора a, если их координаты известны:+ х2; у1+ у2>Решение. Во всех случаях сначала вычтите первую координату вектора a из первой координаты вектора b, чтобы получить координату x искомого вектора. Затем повторите операцию со второй координатой (т.е. y):

Далее рассмотрим такую операцию, как умножение вектора на число. Опять же, вектор a с координатами x
и y
можно разложить на коэффициенты следующим образом:
Напомним, что если два вектора (назовем их a и b) коллинеарны, то обязательно существует число k такое, что

Из равенства (1) и правила умножения вектора на число, описанного выше, вытекают два соотношения между этими координатами:

Если числа x; у1>Аналогично вычисляем координату y:; у2>не равны нулю, то из каждого уравнения можно выразить число k, тогда выражения можно приравнять:

Получаем соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратном направлении — если координаты векторов удовлетворяют производной, то можно смело утверждать, что векторы слиплись.

Примечание. Фраза «тогда и только тогда» означает, что правило работает в обе стороны — из пропорциональности координат следует конгруэнтность векторов, а из конгруэнтности векторов следует пропорциональность координат.
может быть любым числом, так как всегда можно найти такое число k, для которого выполняется условие
Например, если у нас есть вектор. Можно сказать, что он коллинеарен с любым вектором, первая координата которого также равна нулю, а именно,
Но любой вектор, чья x-координата НЕ равна нулю, НЕ коллинеарен с. В частности, он не является коллинеарным с вектором:

Та же логика применима, если не x-координата, а y-координата равна нулю.

Если обе координаты вектора равны нулю, то это нулевой вектор, т.е. точка. Следует помнить, что такой вектор коллинеарен с любым другим вектором.1Задание. Определите, являются ли два вектора коллинеарными, если их координаты равны:1Действия с векторами описываются как в алгебре, так и в геометрии. Сегодня мы рассмотрим, как складывать и вычитать векторы, не зная их координат.
Признак коллинеарности векторов
Представьте, что у нас есть векторы в пространстве и нам нужно их сложить. Эта проблема особенно важна для физиков, поскольку векторные величины, такие как сила, часто прикладываются к одному и тому же телу. Возникает вопрос: как рассчитать результирующий эффект всех этих сил?

Вот где математика, царица наук, приходит на помощь физикам! Чтобы сложить два вектора, нужно сделать следующее:
Складывать векторы можно и другим способом, используя метод параллелограмма:2Задание. Определите, являются ли два вектора коллинеарными, если их координаты равны:2И метод параллелограмма, и метод треугольника предполагают перемещение векторов в пространстве: либо объединение их концов, либо переход от конца одного вектора к началу другого. Извлечение суммы векторов, не имеющих общей точки, невозможно с помощью этих методов.
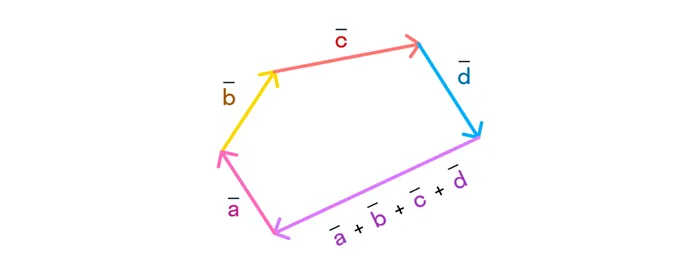
Но что если векторов больше двух? В математике уже есть решение этой проблемы: мы используем метод расширенных треугольников, так называемый «метод многоугольников».

В этом методе мы объединяем конец и начало векторов один за другим, а затем представляем кумулятивный вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего вектора. Лучше всего это видно на рисунке:
Мы продолжаем выполнять различные действия с векторами, на этот раз путем вычитания. Математики знают, что вычитание — это то же самое, что и сложение, только с обратным числом.
То же самое справедливо и для векторов: Вместо вычитания мы можем добавить вектор, противоположный исходному вектору:
Представим разность векторов с помощью уже известного нам правила треугольника:
Вы боитесь запутаться в односторонних и противоположных векторах? Существует отдельное правило для афиры
>1; у2>
2Задание. Определите, являются ли два вектора коллинеарными, если их координаты равны:1

Сложение и вычитание векторов
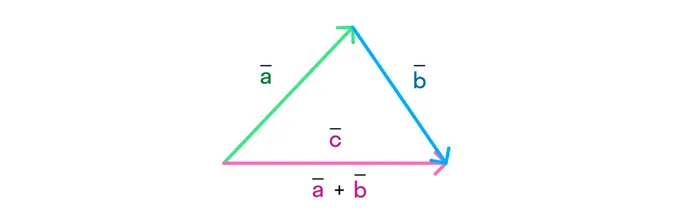
Сложение: метод треугольника
- Отложить начало одного вектора от конца другого.
- Вектор их суммы будет совпадать с вектором, который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
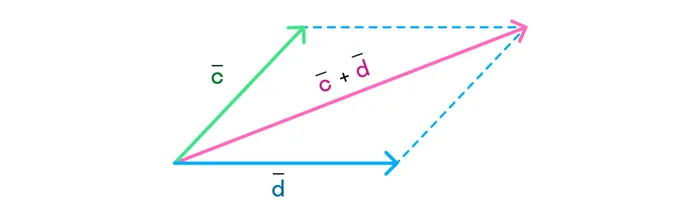
- Совместим между собой концы и
- Отложим от конца вектор, равный
- Отложим от конца вектор, равный
- Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).
- Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Сложение: метод многоугольника
Вычитание векторов
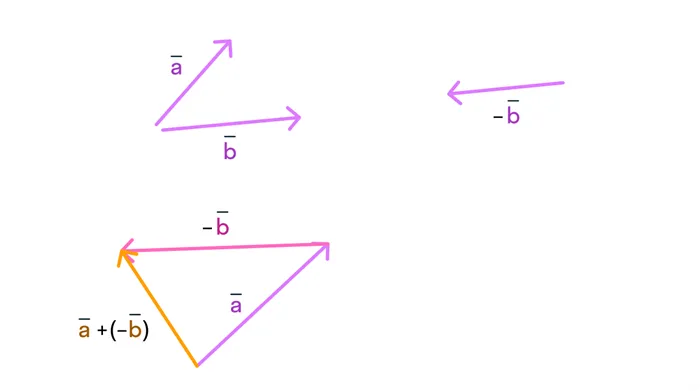
- Отложим один вектор от начала другого.
- Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.

Координаты вектора на плоскости и в пространстве