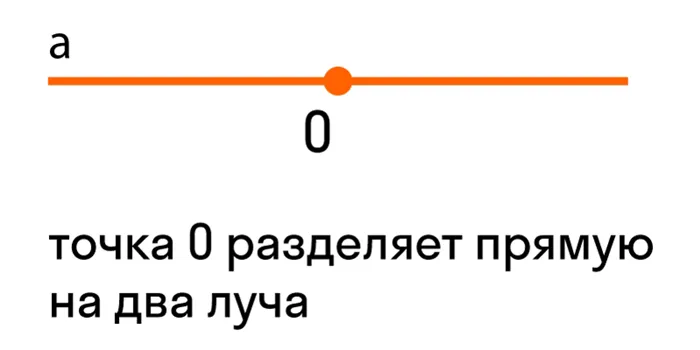
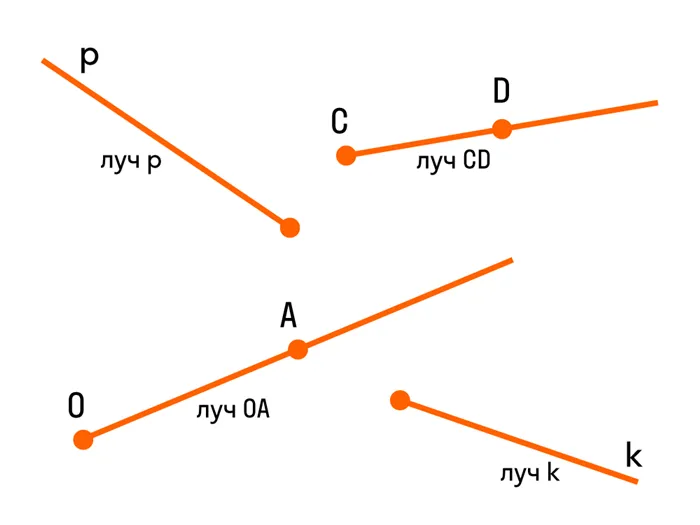
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Этот угол обозначается \( \small ∠mn \) или \( \small ∠O. \). Выбрав точки A и B на сторонах угла, угол можно определить следующим образом: \( \малый &угол;AOB\) или \( \малый &угол;BOA. \).
Геометрическая фигура угол
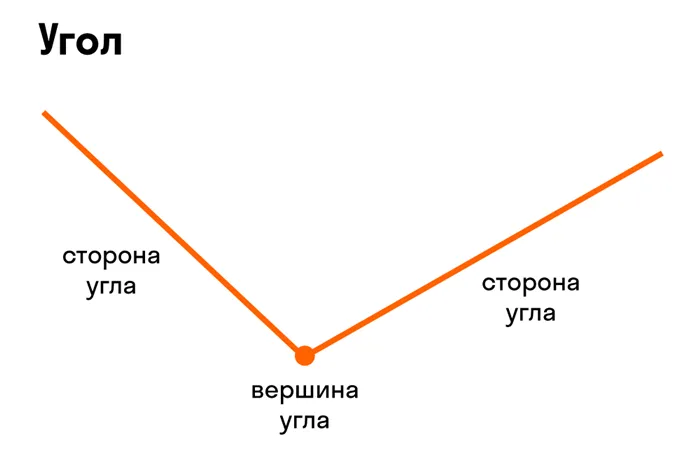
Угол — это геометрическая фигура, образованная двумя лучами с одинаковой начальной точкой. Эта точка называется вершиной угла, а лучи — сторонами угла. Стороны угла делят плоскость на две области, называемые плоскими углами или просто углами. Меньший угол — это внутренний угол, а больший — внешний.
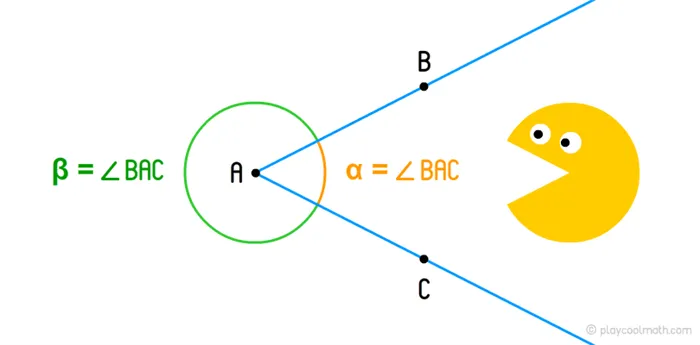
Углы также могут быть представлены тремя точками. Пример: ABC. В этой нотации B — вершина, а A и C находятся на разных сторонах угла. Чтобы упростить и ускорить обозначения, углы обычно представляют строчными греческими буквами: a — альфа, b — бета, c — гамма, i — тета, f — фи и т.д. Угол обозначается символом в виде двух отрезков, представляющих собой угол.
На рисунке два луча AB и AG с вершиной A образуют два угла: a — внутренний угол, b — внешний угол.
Угловая мера
Мера угла позволяет сравнивать углы, т.е. если мы знаем меру угла, мы можем сказать, что этот угол либо больше, либо меньше, либо равен другому. Существуют различные меры углов:
- в градусах, минутах, секундах;
- в радианах;
- в оборотах;
- в градах, минутах, секундах.
В математике наиболее распространен первый тип измерения угла — градусы, минуты, секунды. Давайте поговорим об этом подробнее. Посмотрите на часы, показанные ниже.
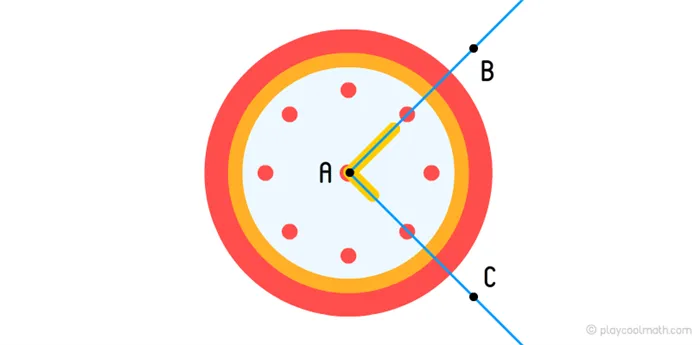
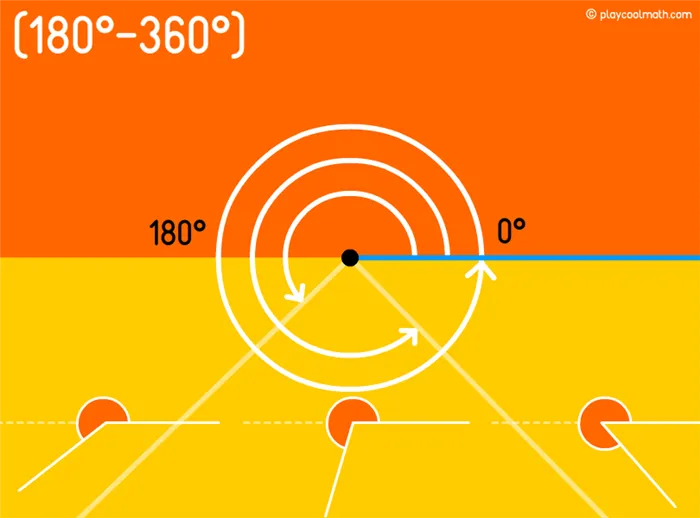
Если внимательно посмотреть на часы, то можно увидеть стрелки часов в виде лучей, начальная точка которых совпадает с центром циферблата. Для полного вращения руки принимается значение 360 градусов. Степень обозначается символом °. На пол-оборота стрелка перемещается на 180° или 180°, на четверть оборота — на 90°. В следующем примере вы можете увидеть, какое время соответствует углу в разное время. Например, 15:00 соответствует 90°, 18:00 — 180°, 21:00 — 270° и 24:00 — 360°. Сумма внешнего и внутреннего углов всегда равна 360°.
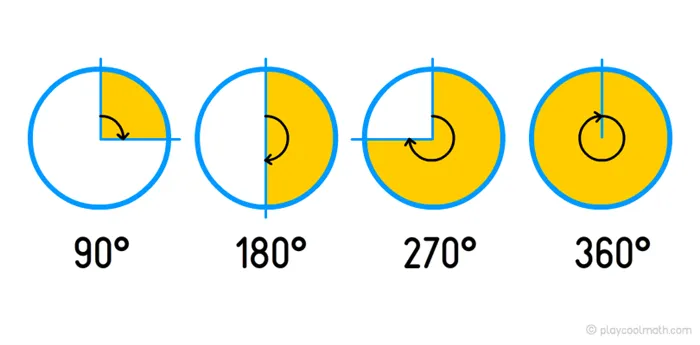
Вы будете подробно изучать угловую меру в других математических предметах: Геометрия и тригонометрия.
Типы Углов
В зависимости от меры угла существуют следующие типы углов:
Нулевой угол
Нулевой угол — это угол, две стороны которого совпадают. Два луча одинакового направления начинаются из вершины. Нулевой угол равен 0°.
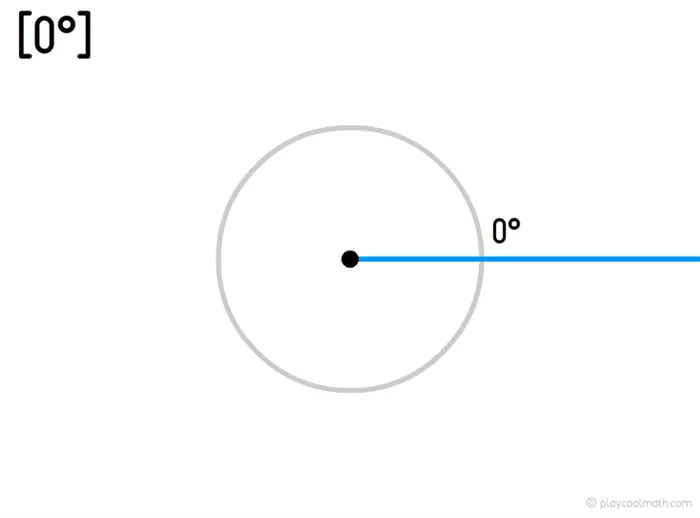
Острый угол
Острый угол — это угол, лежащий между 0° и 90°, где 0 и 90 не входят в это поле.
Острый угол легко запомнить. Все острые предметы имеют острый угол, например.
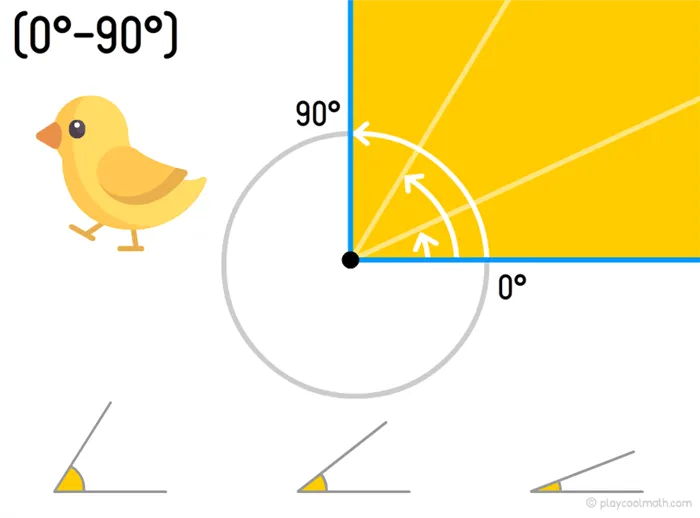
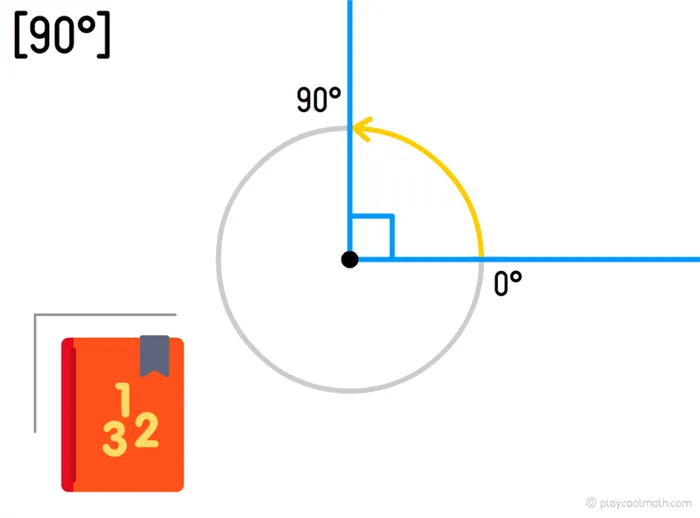
Прямой угол
В зависимости от размера углы можно разделить на следующие типы (рис. 5):
Углы можно сравнить, т.е. определить, равны ли они, или какой угол меньше, а какой больше. Чтобы определить, равны углы или нет, нужно положить один угол на другой так, чтобы сторона одного угла была совмещена со стороной другого угла, а две другие стороны находились по одну сторону от совмещенных сторон. Если две другие стороны также совпадают, то они конгруэнтны, то есть одинаковы. Если они не конгруэнтны, то угол, принадлежащий другому, считается меньшим.
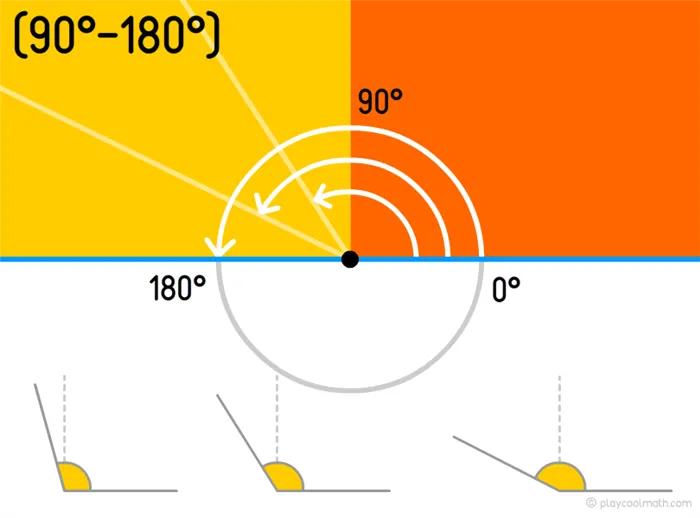
Тупой угол
На рисунках 6a и 6b показаны два угла, 1 и 2. На рисунке 7 угол 2 является частью угла 1, поэтому угол 2 меньше угла 1. Это записывается следующим образом: \( \маленький &угол;2 \lt \угол 1. \).
Косой угол
Измерение углов основано на сравнении с углом, который принимается за единицу измерения. Единицей измерения углов является градус, который представляет собой \( \малую \frac \) часть угла. Положительное число, показывающее, сколько раз градус и его части вписываются в данный угол, называется градусной мерой угла. Для измерения углов используется транспортир (рис. 8).
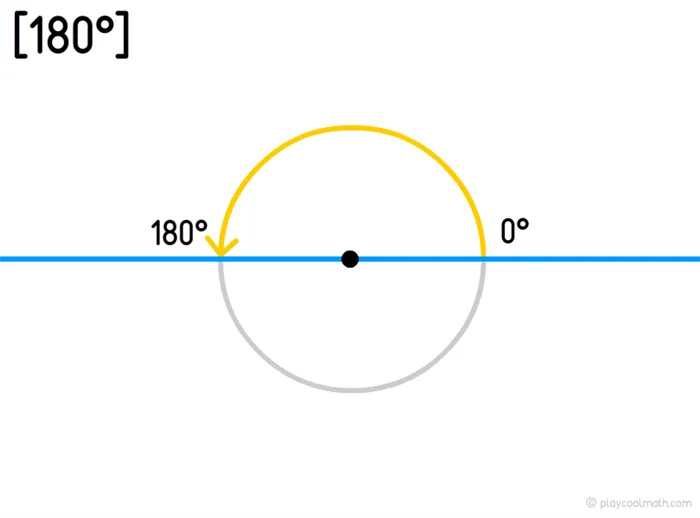
Развёрнутый угол
Для угла AOB, градусная мера которого равна 120°, мы говорим «угол AOB равен 120°» и пишем: \( \малый &угол;AOB=120°. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \малая \Frac \) часть степени называется тонкой частью и обозначается: » ‘ «. \( \малая \Frac \) часть минуты называется секундой и обозначается: » ‘ «. Если мера угла AOB равна 56 градусов, 6 минут и 43 секунды, то пишется: \( \малый угол AOB=56°6’43»\).
Выпуклый угол
Обратите внимание, что равные углы имеют равные градусы. Если углы разные, то меньший угол имеет меньшую градусную меру.
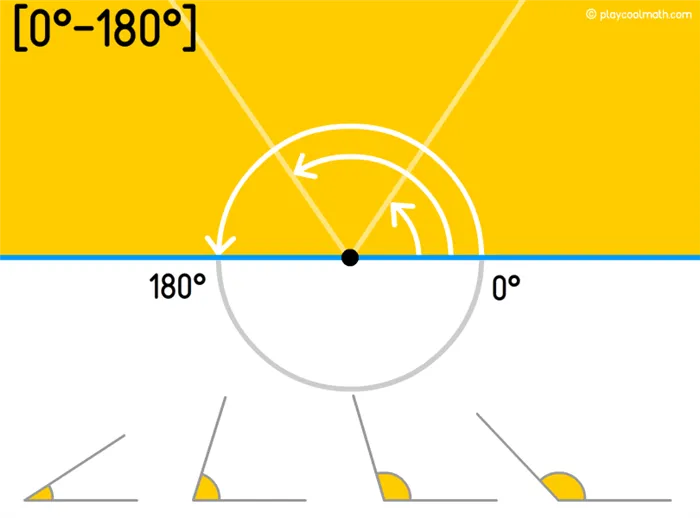
Невыпуклый или вогнутый угол
Теперь давайте разберемся, что означает сходство:
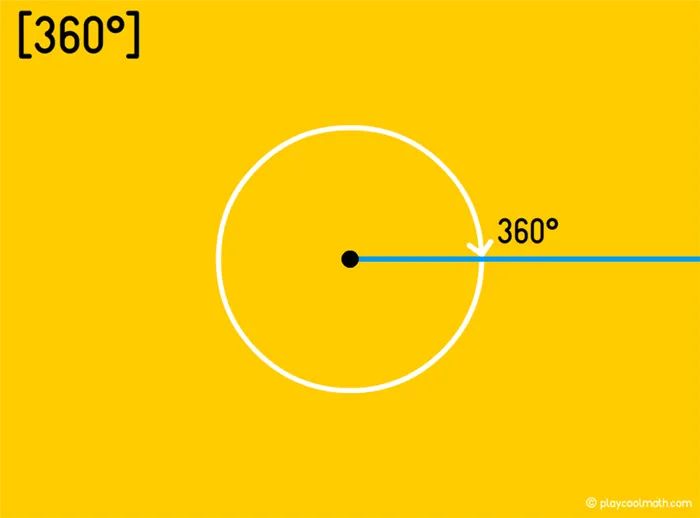
Полный угол
Если треугольники похожи, но отличаются только размером, то сходство треугольников помогает
Коэффициент подобия — это число, на которое отличаются стороны треугольников
Если ABC похож на A1B1C1, то выполняется равенство, где k — коэффициент сходства.
- Нулевой угол — 2;
- Острый угол — 3;
- Прямой угол — 2;
- Тупой угол — 2;
- Косой угол — 6;
- Развёрнутый угол — 1;
- Выпуклый угол — 10;
- Вогнутый угол — 1;
- Полный угол — 1;
Типы углов
Если треугольники подобны, то отношение их площадей равно квадрату коэффициента подобия
- Нулевой угол (0°). Стороны угла совпадают. Его внутренняя область пустое множество.
- Острый угол (больше 0° и меньше 90°)
- Прямой угол (90°). Стороны прямого угла перпендикулярны друг другу.
- Тупой угол (больше 90° и меньше 180°).
- Развернутый угол (180°).
- Невыпуклый угол (от 0° до 180° включительно).
- Выпуклый угол (больше 180° и меньше 360°).
- Польный угол (360°).
Сравнение углов
Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы, входящие между этими сторонами, равны, то эти треугольники подобны.
Если два угла треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Градусная мера угла
Если стороны треугольника равны сторонам другого треугольника, то они конгруэнтны.
Площадь треугольника, когда известны высота и основание, на котором он построен.
Площадь треугольника с двумя известными сторонами и углом между ними.
Содержание раздела
- Точка (геометрия)
- Прямая
- Луч (геометрия)
- Угол
- Отрезок
- Серединный перпендикуляр к отрезку
- Ломаная
- Пропорциональные отрезки
- Аксиома параллельных прямых
- Смежные углы. Свойства смежных углов
- Вертикальные углы. Свойства вертикальных углов
- Перпендикулярные прямые
- Перпендикуляр к прямой
- Параллельные прямые. Признаки параллельности прямых
- Теоремы об углах, образованных двумя параллельными прямыми и секущей
- Биссектриса угла. Свойства
- Теорема Пифагора онлайн
- Теорема, обратная теореме Пифагора
- Теорема Фалеса. Доказательство
- Треугольники. Признаки равенства треугольников
- Подобные треугольники. Признаки подобия треугольников
- Биссектриса треугольника онлайн
- Серединные перпендикуляры к сторонам треугольника
- Теорема о биссектрисе треугольника. Доказательство
- Высота треугольника онлайн
- Теорема Стюарта. Доказательство
- Теорема синусов. Доказательство
- Теорема косинусов. Доказательство
- Решение треугольников онлайн
- Прямоугольный треугольник. Онлайн калькулятор
- Равнобедренный треугольник. Онлайн калькулятор
- Сумма углов треугольника
- Внешний угол треугольника
- Виды треугольников
- Соотношения между сторонами и углами треугольника
- Неравенство треугольника
- Средняя линия треугольника
- Теорема Менелая
- Окружность, описанная около треугольника
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около прямоугольного треугольника онлайн
- Окружность, вписанная в треугольник
- Радиус вписанной в треугольник окружности онлайн
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- Радиус вписанной окружности в равносторонний треугольник онлайн
- Радиус вписанной окружности в прямоугольный треугольник онлайн
- Окружность и круг. Онлайн калькулятор
- Взаимное расположение прямой и окружности
- Касательная к окружности
- Центральный угол окружности. Градусная мера дуги окружности
- Вписанный угол окружности
- Квадрат. Онлайн калькулятор
- Прямоугольник. Онлайн калькулятор
- Параллелограмм
- Ромб
- Сторона ромба онлайн
- Высота ромба онлайн
- Площадь ромба онлайн
- Диагонали ромба онлайн
- Трапеция. Определение, виды, свойства
- Четырехугольник
- Четырехугольник, вписанный в окружность
- Окружность, вписанная в четырехугольник
- Многоугольник
- Площадь треугольника онлайн
- Площадь прямоугольного треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
- Площадь квадрата онлайн
- Площадь прямоугольника онлайн
Признаки равенства треугольников:
- Треугольники равны по двум сторонам и углу между ними
- Треугольники равны по стороне и двум прилежащим к ней углам
- Треугольники равны по трём сторонам
Площадь правильного треугольника с известными перпендикулярами
Площадь правильного треугольника, когда известна только сторона
С помощью формулы Герона можно вычислить площадь треугольника, если известны его стороны
Площадь треугольника, если известны радиус и радиус эндоцикла.
Площадь треугольника, если известны стороны и радиус окружности
Признаки подобия треугольников:
- По двум углам
- По трём сторонам
Площадь треугольника