Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы. Что такое синус и косинус?

Тангенс числа t — это отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

ТРИПЛЕЙНЫЕ ФУНКЦИИ являются одним из классов элементарных функций.

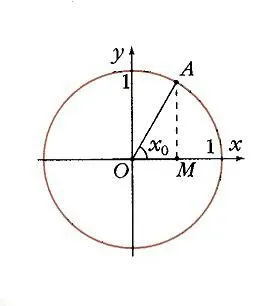
Если мы нарисуем единичную окружность с началом координат в центре и зададим любое значение аргумента x₀и отсчитываем угол x по оси ox_0,существует точка A на единичной окружности (рис. 1), а ее проекция на ось Ox — M. Длина отрезка OM равна абсолютной величине отклонения от точки A. Заданное значение аргумента x₀сравнивается со значением функции y = cos x₀как отклонение от точки A. Аналогично, точка B ( x₀; у₀) принадлежит графику функции y = cos x (рис. 2). Если точка A находится справа от оси O, косинус положителен, если слева — отрицателен. В обоих случаях точка A не может покинуть круг. Поэтому косинус находится межд у-1 и 1:

-1 = cos x = 1.

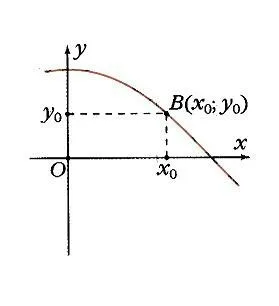
Дальнейший поворот на любое кратное 2 p возвращает точку A в ту же точку. Поэтому функция y = cos x является периодической, ее период равен 2 p :

cos ( x + 2 p ) = cos x.

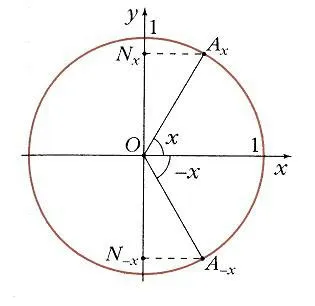
Даны два значения аргумента с одинаковой абсолютной величиной, но противоположным знаком, x и — x, на окружности расположены соответствующие точки A_xи А_-x. Как и на рис. 3, их проекцией на ось O является одна и та же точка M .

cos (- x ) = cos ( x ),

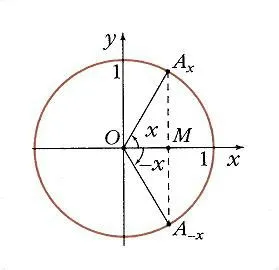
Т.е. косинус является четной функцией, f (- x ) = f ( x ) .

Поэтому мы можем исследовать свойства функции y = cos x в интервале 0, p, а затем рассмотреть ее гладкость и периодичность.

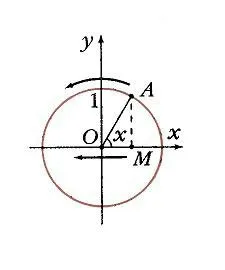
При x = 0 точка A лежит на оси O, ее экстремум равен 1, поэтому cos 0 = 1. При увеличении x точка A движется вверх и влево по окружности, ее проекция, естественно, только влево, и при x = p /2 косинус становится равным 0. В этой точке точка A поднимается на максимальную высоту, а затем продолжает двигаться влево, но уже вниз. Его дивергенция продолжает уменьшаться, пока не достигнет наименьшего значени я-1 при x = p. Таким образом, в интервале 0, p функция y = cos x монотонно убывает от 1 д о-1 (рис. 4, 5).

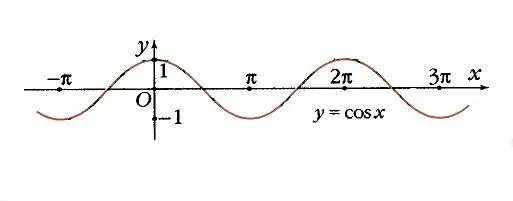
Из соотношения косинусов следует, что функция монотонно возрастает о т-1 до 1 в интервале — p, 0 и принимает нулевое значение при x = — p /2. Если взять несколько периодов, то получится волнистая кривая (рис. 6).

Функция y = sin х.

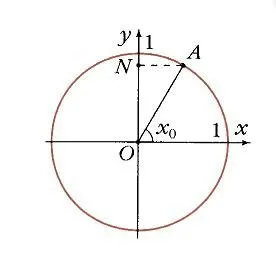
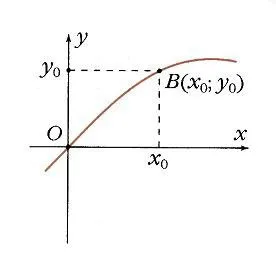
В единичном круге угол x₀соответствует точке A (рисунок 7), а ее проекция на ось O равна N. Значение функции y₀= sin x₀определяется как линия, проведенная из точки A. Точка B (угол x₀, у₀) принадлежит графику функции y = sin x (рис. 8). Ясно, что функция y = sin x является периодической, ее период равен 2 p :

sin ( x + 2 p ) = sin ( x ).

Для двух значений аргумента, x и -, проекции соответствующих точек A_xи А_-xна оси O s

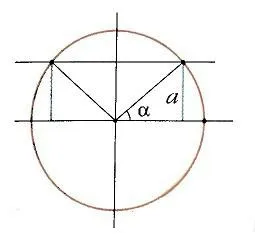
Геометрический смысл равенства показан на рисунке 11. Здесь x — половина дуги AB, а sin x — половина соответствующей строки. Очевидно, что чем ближе точки A и B, тем ближе длина струны к длине дуги. Из этого же рисунка нетрудно вывести неравенство

|sin x | » x для малых x .

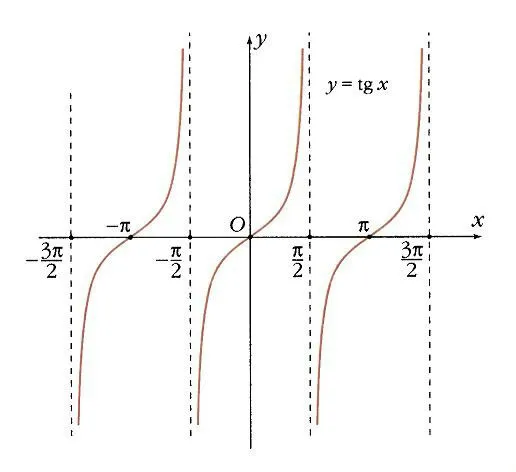
Функции y = tg x, y = ctg x. Две другие тригонометрические функции, тангенс и котангенс, проще определить как соотношения синуса и косинуса, которые мы уже знаем:

Как и синус и косинус, тангенс и котангенс являются периодическими функциями, но их период равен p, т.е. они вдвое короче синуса и косинуса. Причина ясна: когда синус и косинус меняют знак, их отношение не меняется.

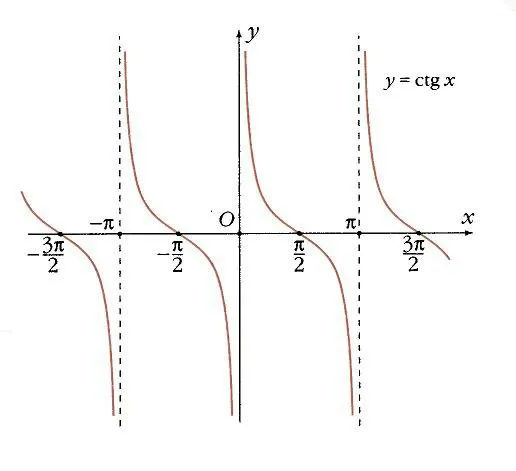
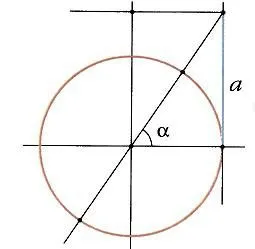
Поскольку знаменатель тангенса — косинус, тангенс неопределен в точках, где косинус равен 0 — если x = p /2 + k p. Во всех остальных точках он монотонно увеличивается. Линии x = p /2 + k p вертикально асимптотичны к касательной. В точках k p тангенс и угловой коэффициент равны 0 и 1 соответственно (рис. 12).

Котангенс неопределен, когда синус равен 0 (когда x = k p ). В других точках она монотонно убывает, и прямые x = k p являются ее вертикальными асимптотами. В точках x = p /2 + k p когерентность становится равной 0, а угловой коэффициент в этих точках раве н-1 (рис. 13).

Функция называется четной, если f (- x ) = f ( x ). Функции косинус и синус являются четными, а синус, тангенс, котангенс и косинус — нечетными функциями:

sin (-α) = — sin α

tg (-α) = — tg α

cos (-a) = cos α

ctg (-α) = — ctg α

Четность и периодичность.

сек (-α) = сек α

cosec (-α) = — cosec α	Свойство четности вытекает из симметрии точек P
и P	(рис. 14) относительно оси x. При такой симметрии расположение точек меняет знак (( x ; y ) меняется на ( x ; -u )). Все функции периодичны; синус, косинус, секанс и косинус имеют период 2 p, тангенс и котангенс имеют период p :
sin (a + 2 kπ ) = sin a	cos (α + 2 kπ ) = cos α

tg (α + kπ ) = tg α_actg (α + kπ ) = ctg α_{— a}sec (α + 2 kπ ) = sec α

cosec (α + 2 kπ ) = cosec α	Периодичность синуса и косинуса обусловлена тем, что все точки P
совпадают при k = 0, ±1, ±2, …, а периодичность касательной и котангенса вытекает из того, что точки P	падают поочередно на две диаметрально противоположные точки окружности и дают одну и ту же точку на оси касания.
Основные свойства тригонометрических функций можно свести в таблицу:	Функция

Функция_{a + 2k p}Определение функции_{a +k p}Эквивалентность

диапазоны монотонности (k = 0, ± 1, ± 2, …)

sin x	— Ґ	-1, +1	странно	увеличивается до x O ((4 k — 1) p /2, (4 k + 1) p /2), уменьшается до x O ((4 k + 1) p /2, (4 k + 3) p /2)
cos x	— Ґ	-1, +1	но к	Из этого следует, что тангенс угла равен отношению синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Независимо от этого, следует отметить, что тригонометрические тождества	— Ґ	-1, +1	Подготовительные курсы Skysmart по математике придадут вам уверенности и помогут подтянуть знания перед экзаменом.	Насколько очевидной кажется связь между тождествами, рассмотренными ранее, настолько же очевидной кажется связь между тангенсом и котангенсом угла.
Это тождество применимо и действительно для любого угла a, значение которого не равно π/2 * z, где z — любое целое число. В противном случае функции не определены.	Как и любое другое тригонометрическое тождество, это необходимо доказать. Доказательство очень простое.	tg a * ctg a = 1.	но к	Если числа α и β взаимно обратны, это означает, что число α является обратным числу β, а число β является обратным числу α. Это также означает, что число a является обратным числу b, а число b является обратным числу a. Короче говоря, в обоих направлениях.
Обратные числа — это два числа, произведение которых равно 1.	Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.	tg a * ctg a = 1.	но к	tg 2 a + 1 =
Сумма квадрата тангенса угла и единицы равна числу, соответствующему обратному квадрату косинуса этого угла.	Как и любое другое тригонометрическое тождество, это необходимо доказать. Доказательство очень простое.	Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.	Подготовительные курсы Skysmart по математике придадут вам уверенности и помогут подтянуть знания перед экзаменом.	Хорошо бы выучить все формулы и запомнить формулировки тождеств. Для этого сохраните таблицу основных формул.
Основные тригонометрические уравнения	Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.	Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.	но к

Тангенс и котангенс через синус и косинус

• Синус угла — это ордината y.
• Косинус угла — это абсцисса x.
• Тангенс угла — это отношение ординаты к абсциссе.
• Котангенс угла — это отношение абсциссы к ординате.

• tg α =
• ctg α =

• Например, выражение + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.

Связь между тангенсом и котангенсом

• Тождество записывается в следующем виде: tg α * ctg α = 1.

ctg α = x/y

Отсюда следует, что tg α * ctg α = y/x * x/y = 1

Преобразовываем выражение, подставляем, получаем:

Тангенс и косинус, котангенс и синус

1. Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
2. В результате деления получаем формулу tg 2 α + 1 =
3. Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество: 1 + ctg 2 α =
4. Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 = + π + z, где z — это любое целое число.
5. А тригонометрическое тождество 1 + ctg 2 α =