Умножение или произведение натуральных чисел, их свойства. Что такое произведение в математике?

Произведением последовательности, состоящей из одного числа, является само число; произведение без факторов называется пустым произведением и равно 1.

Умножение

Умножение целого числа на другое — это повторение одного числа столько раз, сколько единиц содержит другое число. Повторить число — значит взять его сумму много раз и определить сумму.

Умножение целых чисел — это операция взятия суммы одного числа столько раз, сколько единиц у другого числа, и нахождения суммы этих сумм.

Умножить 7 на 3 означает взять число 7 три раза в сумме и найти сумму. Необходимая сумма равна 21.

Умножение — это сложение одинаковых сумм.

Данные при умножении называются множителем и множителем, а желаемый результат — произведением .

В приведенном примере данными являются множитель 7, множитель 3 и искомое произведение 21.

Множитель. Множитель — это число, которое умножается или повторяется на сумму. Множитель выражает значение равных сумм.

Множитель. Множитель указывает, как часто множитель повторяется на сумму. Множитель указывает на количество равных сумм.

Производная Производная — это число, которое получается в результате умножения. Это сумма равных сумм.

Множитель и коэффициент умножения называются производителями.

При умножении целых чисел одно число умножается столько раз, сколько единиц содержится в другом числе.

Знак умножения. Эффект умножения обозначается символом × (косвенный крест) или. (точка). Поставьте знак умножения между множителем и множителем.

Повторить число 7 три раза в качестве слагаемого, чтобы найти сумму 7, умноженную на 3. Вместо записи

Письмо с символом умножения короче:

7 × 3 ή 7 — 3.

Умножение — это сокращенное сложение равных количеств.

Символ ( × ) был введен Отредом (1631), а символ. Кристианом Вольфом (1752).

Связь между данными и определяемым числом выражается умножением

7 × 3 = 21 ή 7 — 3 = 21

Семь, умноженное на три, равно 21.

Чтобы получить произведение 21, мы должны повторить 7 три раза.

Чтобы получить коэффициент умножения 3, единицу нужно повторить три раза.

Это дает нам еще одно определение умножения: умножение — это операция, при которой умножение подобно составлению множителя, потому что умножение — это составление единицы.

Основное свойство произведения

Продукт не меняется при изменении порядка производителей.

Доказательство. Умножить 7 на 3 — значит повторить 7 три раза. Заменив 7 на сумму 7 единиц и s

Под этой строкой вы должны подписать ряд чисел, которые представляют собой произведение этих чисел, умноженное на 2. Этот ряд чисел получается путем прибавления каждого числа в первом ряду к самому себе. Переходите от второго ряда чисел по порядку к 3, 4 и так далее. Каждый последующий ряд получается из предыдущего путем сложения чисел в первом ряду.

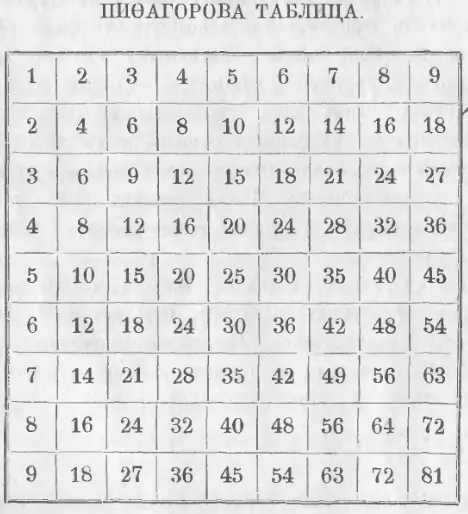
Если вы продолжите до строки 9, то получите таблицу Пифагора в следующем виде.

Умножение однозначных чисел. Таблица Пифагора

Чтобы найти произведение двух однозначных чисел с помощью этой таблицы, найдите одно произведение в первой горизонтальной строке, а другое — в первом вертикальном столбце; затем найдите искомое произведение на пересечении соответствующих столбца и строки. Поэтому произведение 6 × 7 = 42 находится на пересечении строки 6 и столбца 7. Произведение нуля на число и числа на нуль всегда дает нуль.

Поскольку произведение числа на 1 дает то же самое число, а изменение порядка множителей не изменяет произведение, все различные произведения двух однозначных чисел, которые необходимо рассмотреть, сведены в следующую таблицу:

Произведения однозначных чисел, не включенных в эту таблицу, получаются из данных путем изменения только порядка множителей в них; т.е. 9 × 4 = 4 × 9 = 36.

Мы дали каждому из 5 наших друзей по два яблока. Математически запись будет выглядеть так: 2⋅5. Или мы дали по 5 яблок двум друзьям. Математически запись будет выглядеть так: 5⋅2. В первом и втором случае мы даем одинаковое количество яблок, которое равно 10 яблокам.

Если умножить 2⋅5=10 и 5⋅2=10, результат не изменится.

Свойство постпозитивного закона умножения: произведение не меняется от перемены мест множителей. m ⋅ n =n⋅ m

Рассмотрим пример:

(2⋅3)⋅4=6⋅4=24 или 2⋅(3⋅4)=2⋅12=24, (2⋅3)⋅4=2⋅(3⋅4) ( a ⋅ b ) ⋅ c = a ⋅( b ⋅ c )

Свойство комбинаторного закона умножения: чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а затем умножить полученное произведение на второй множитель.

Умножение смешанных дробей. Как умножать смешанные дроби?

Переместительный закон умножения.

Если вы измените несколько множителей и заключите их в скобки, результат или произведение не изменится.

Эти законы применимы к любому натуральному числу.

Пример: 7⋅1=7 или 1⋅7=7 a ⋅1=a или 1⋅ a = a Когда натуральное число умножается на единицу, произведение всегда одно и то же число.

Сочетательный закон умножения.

6⋅0=0 или 0⋅6=0 a ⋅0=0 или 0⋅ a =0 При умножении натурального числа на ноль произведение равно нулю.

Вопросы об умножении:

Что такое произведение чисел? Ответ: произведение чисел или умножение чисел — это выражение m⋅n, где m — сумма, а n — количество повторений этой суммы.

Какова цель

Задача 2: Учитель рисования попросил своих восемь учеников подготовить к уроку по семь карандашей. Сколько карандашей было у детей? Решение: Вы можете посчитать сумму задачи. У первого ученика было 7 карандашей, у второго — 7 карандашей и т.д. 7+7+7+7+7+7+7+7+7+7=56 Предложение сложное и длинное, поэтому заменим сумму произведением. 7⋅8=56 Ответ: 56 карандашей.

Умножение любого натурального числа на единицу.

Отменить ответ

Вы должны войти в систему, чтобы оставить комментарий.

Важной математической операцией является произведение чисел. Что скрывается за такими терминами, как произведение, умножение. Именно об этом и пойдет речь в нашей статье. Давайте лучше начнем с банальных вещей. Когда у нас много вещей, хранить их в виде информации довольно сложно. Каким-то образом мы должны компактно их уменьшить. Допустим, у нас в гардеробе больше двух пар носков, то есть 15. Как мы можем записать их на бумаге? Да, конечно, мы можем написать 2+2+2. И так далее, пока мы не добавим к их количеству число два, связанное с парой носков, которое равно 15. Но это, понятно, непрактично, особенно когда понимаешь, что речь идет не только о носках в шкафу, но и о хранении в магазине! И здесь проще выразить это словами, например, так. У нас есть две пары носков, которые брали несколько раз!

Именно здесь происходит волшебство перехода от обычной суммы к произведению, когда мы берем число несколько раз. Пришло время дать определение.

Произведение двух чисел — это не что иное, как сумма одного числа с суммой другого числа.

Снова. Если произведение равно C, то номинал одного из чисел a равен b, умноженному на b, и будет произведением. Вы можете написать его следующим образом

C=a1+a2+a3+a4. +ab, где 1,2,3,4. b будет индексом, указывающим на то, чем является число a, и не более того!

Пример Найдите произведение чисел:

1) 1.2⋅3 ;

Ответ: 1,2⋅3=3,6

2) 4⋅5⋅13

Ответ: 4⋅5⋅13=260

Добавить комментарийКоммутативность: n⋅m=m⋅n Коррелятивность: (n⋅m)⋅k=n⋅(m⋅k) Из этих свойств можно сделать вывод, что значение коэффициента не меняется при перестановке множителей.

Пример Найдите произведение чисел удобным способом:

Что такое произведение в математике

1) 5⋅17⋅2 ; 2) 7⋅2⋅15⋅5

Решение. По свойству умножения имеем:

Определение произведения чисел

5⋅17⋅2=(5⋅2)⋅17=10⋅17=170 7⋅2⋅15⋅5=(7⋅(2⋅15))⋅5=(7⋅30)⋅5=210⋅5=1050 Ответ.

5⋅17⋅2=170 7⋅2⋅15⋅5=1050

Когда устное умножение чисел затруднено, используется умножение в столбик. Умножение в столбик можно применять к большим натуральным или десятичным числам.

Пример Найдите произведение чисел

1) 156⋅32 ; 2) 4,71⋅3,1

Решение. Запишите числа, которые нужно перемножить, в столбики. Сначала умножьте единицы второго числа на первое число и напишите

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Свойства произведения чисел

Эта информация доступна для зарегистрированных пользователей

Определение: квадратом числа a называется число \(\mathbf\), для которого выполняется: \(\mathbf\)

Возможно, вы уже задаетесь вопросом, почему «квадрат»? Давайте сразу ответим на этот вопрос.

Чтобы определить площадь прямоугольника, нужно перемножить длины двух противолежащих сторон.

Другими словами, площадь квадрата равна квадрату длины стороны.

Мы уже рассмотрели немного геометрии, с которой вы разберетесь позже, а пока давайте рассмотрим примеры нахождения квадратов.

Пример:

Найдите квадрат числа 3.

Считать по определению, умножая 3 на себя:

Другой пример положительного числа: найдите квадрат числа 12:

Аналогично, мы умножаем число на само себя:

А с нулем все просто: любое число, умноженное на 0, дает 0, и сам 0 при умножении на 0 дает 0:

Теперь давайте посмотрим, что произойдет, если мы измерим квадрат отрицательного числа:

Давайте измерим квадрат \(\mathbff\):

Обратите внимание, что мы перемножали отрицательные числа — то есть, по сути, мы просто взяли квадрат коэффициента конкретного отрицательного числа.

Правило: квадрат отрицательного числа равен квадрату коэффициента отрицательных чисел.

Возведение числа в квадрат

Также обратите внимание, что квадрат всегда неотрицателен.

Доказательство:

Поэтому мы рассмотрели все возможные случаи, и во всех из них квадрат был неотрицательным числом, то есть положительным.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Мы уже знаем, что произведение отрицательного числа на положительное дает отрицательное число.

Но что если использовать его наоборот?

Например, существует отрицательное число \(\mathbff\).

Заметьте, что оно равно \(\mathbff\).

Также обратите внимание, что квадра т-1 равен 1.

Таким образом, для номеров продуктов мы можем менять и переставлять знаки хитроумным образом.

Например, был такой продукт:

Конвертируя, мы можем оставить только «минус», ср:

Для наглядности мы теперь будем ставить вс е-1 в начало, но это не обязательно:

Каждая пара минусовых единиц дает единицу. В данном случае есть три единицы с минусом, поэтому две из них составляют единицу, а третья остается:

Подумайте, что это значит для нас. Ответ заключается в том, что теперь знак выражения стал более понятным: мы видим произведени е-1 и произведение положительных чисел, которое является положительным числом.

Теперь мы можем сказать, что ответ — отрицательное число.

Правило: произведение многих чисел отрицательно тогда и только тогда, когда нечетное число его множителей отрицательно и ни один множитель не равен нулю.

Оговорка о нуле важна, поскольку если один из множителей равен нулю, то все выражение равно нулю и, следовательно, неотрицательно.

Иногд а-1 исчезает совсем. Это происходит в том случае, если имеется четное количество отрицательных множителей.

Если число в квадрате положительно, то квадрат положительного числа равен произведению положительных чисел и даст результат больший нуля.
Если число, от которого берется квадрат, равно нулю, то и квадрат равен нулю, что удовлетворяет определению неотрицательности.
Если же число, от которого берется квадрат, отрицательно, квадрат будет являться произведением двух отрицательных чисел, то есть числом положительным.

Пример:

Также обратите внимание, что квадрат всегда неотрицателен.

Доказательство:

Представление отрицательного числа как произведения

Эта информация доступна зарегистрированным пользователям

Поэтому в данном случае мы можем перефразировать это выражение следующим образом:

Это также позволит нам преобразовать вычитание отрицательного числа в сложение положительного. Действительно:

Интересно проследить, как развивалась математика в Древней Руси.

В шестнадцатом веке, с приходом к власти Петра Великого (1672-1725), в России была создана система образования, которая постепенно интегрировалась в мир и произвела множество открытий.

Однако до этого времени существовали и математические знания, о которых мы сейчас поговорим.

Как и во всем мире, потребность в математике определялась экономикой.

По этой причине одними из первых денежных единиц были домашние животные и шкуры.

Например, были косари (куски кожи), куны (от слова «куница») и ногаты.

Позже люди стали считать в гривнах: одна гривна, равная 50 граммам серебра, была эквивалентна 50 резанам, 25 кунатам или 20 ногатам.

И только позднее, с XIV века, начался переход к рублю, который тогда представлял собой круглое серебряное изделие весом 205 граммов.

Заметьте, что оно равно \(\mathbff\).

Также обратите внимание, что квадрат всегда неотрицателен.

Доказательство:

Книга «Практический счет, по которому каждый, кто покупает или продает, может узнать количество всевозможных вещей», изданная в 1682 году, уже своим названием говорит о том, что она предназначалась не только для ученых или неспециалистов, но и для торговцев.

При Петре I были созданы школы, приглашены иностранные специалисты, и наука достигла больших успехов.

Также обратите внимание, что квадрат всегда неотрицателен.

Доказательство:

Дополнительная информация

Продукты, которые сравниваются с другими типами алгебраических структур, включают:

Некоторые из перечисленных выше произведений являются примерами общего понятия внутреннего произведения в теории моноидальных категорий; другие описываются общим понятием произведения в теории категорий.

Все предыдущие примеры являются частными случаями или примерами общего понятия продукта. Для общей трактовки понятия продукта см. продукт (теория категорий), который описывает способ, которым два объекта одного типа объединяются для создания объекта, возможно, другого типа. Но в теории категорий есть и это:

пядь равнялась расстоянию между концами разведенных большого и указательного пальца
локоть равнялся расстоянию от кончиков пальца до локтя
сажень была косой и маховой: маховая между разведенными с сторону руками, косая между ногой и отведенной вверх рукой

Также обратите внимание, что квадрат всегда неотрицателен.

Доказательство:

Пустой товар

то Декартово произведение наборов
то прямое произведение групп, а также полупрямой продукт, вязать изделие и венок
то бесплатный продукт групп
то произведение колец
то продукт идеалов
то произведение топологических пространств3
то Фитиль продукт из случайные переменные
то колпачок, чашка, Massey и наклонный продукт в алгебраической топологии
то разбить продукт и сумма клина (иногда называемый продуктом клина) в гомотопия

Товары в теории категорий

то волокнистый продукт или откат,
то Категория продукта, категория, которая является продуктом категорий.
то сверхпродукт, в теория моделей.
то внутренний продукт из моноидальная категория, который отражает суть тензорного произведения.

Другие продукты

Функции интеграл продукта (как непрерывный эквивалент произведения последовательности или как мультипликативная версия нормального / стандартного / аддитивного интеграла. Интеграл произведения также известен как «непрерывный продукт» или «умноженный».
Комплексное умножение, теория эллиптических кривых.

Тензорное произведение Делиня абелевых категорий
Неопределенный продукт
Бесконечный продукт
Итерированная двоичная операция
Умножение — Арифметическая операция

Умножение или произведение натуральных чисел, их свойства. Что такое произведение в математике?