Добро пожаловать в OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я являюсь владельцем и автором этого сайта, я написал весь теоретический материал, а также разработал онлайн упражнения и калькуляторы, которые вы можете использовать для изучения математики.
По какой формуле вычисляется объем прямоугольного параллелепипеда?
Параллелепипед — это многогранник, состоящий из шести четырехугольников с попарно параллельными гранями. Существуют различные типы параллелепипедов в зависимости от того, на каком типе четырехугольника они основаны. Давайте посмотрим, что это такое и чем они отличаются. Мы научимся определять площадь и объем прямоугольных и наклонных параллелепипедов, используя знакомые формулы.
Кубоид или прямоугольник — это шестиугольный многогранник с прямоугольниками в основании. Грани, обращенные друг к другу, параллельны друг другу, а грани, сходящиеся к вершине, перпендикулярны друг другу. Ребра, выходящие из одной вершины, называются размерами.
Свойства геометрического твердого тела:
- Диагонали многогранника в месте пересечения делятся на равные отрезки.
- Место пересечения диагоналей – центр симметрии геометрического тела.
- Размеры противоположных граней равны.
- Квадрат диагонали равен сумме квадратов измерений.
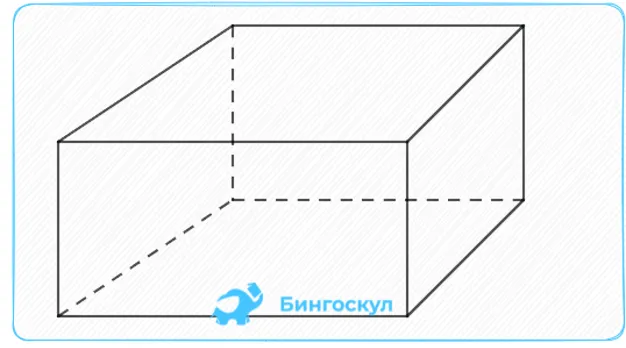
Рассмотрим формулы для объема кубоида и его площади.
Как найти площадь параллелепипеда
Площадь — это числовая характеристика плоской фигуры, которая показывает, сколько квадратов с длиной стороны 1 помещается на поверхности. Она рассчитывается как сумма площадей шести прямоугольных граней.
S = 2 (ab + bc + ac),
где: ab, bc и ac — площади поверхностей.
Поскольку стороны парные, полученная сумма умножается на два.
Пример: У нас есть твердый с размерами:
a = 3, b = 4 и c = 5 см.
Общая площадь поверхности равна:
S = 2 * (3*4 + 4*5 + 5*3) = 2 * (12 + 20 +15) = 2 * (47) = 94 см.
Объем параллелепипеда
Объем — это числовая характеристика тела, отражающая занимаемое им пространство. Он определяется как количество кубов со стороной один, которые помещаются в многоугольник.
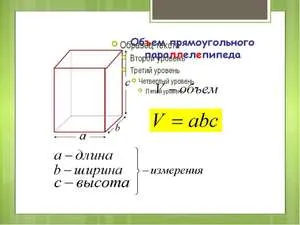
Объем кубоида вычисляется по формуле: V = a * b * c, где
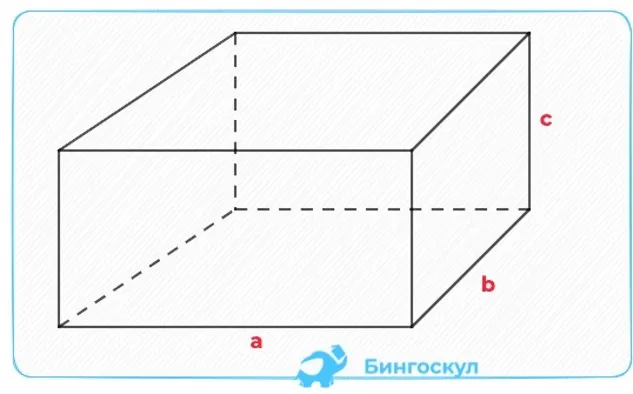
a, b, c — размеры измерений от точки или длина, ширина и высота многогранника.
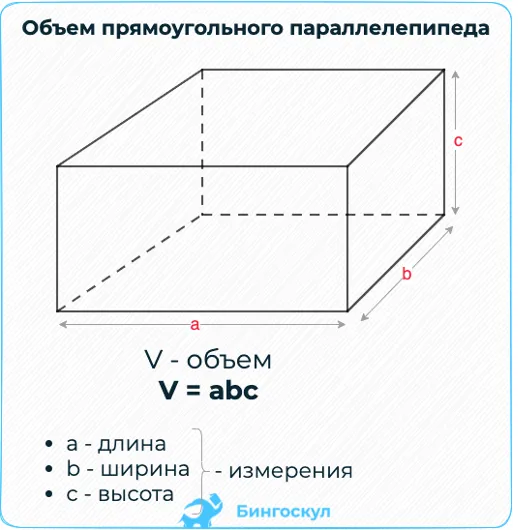
Чтобы найти объем кубоида по приведенной формуле, подставьте размеры граней многоугольника, например:
- высота – 4 см;
- ширина – 3 см;
- глубина – 5 см.
V = 4* 3 * 5 * 5 = 60 см3 .
Измеряется в кубических единицах — сантиметрах, метрах и т.д. или литрах: 1 литр равен 1 десятичному кубическому метру.
Физическая концепция объема проста:
- по высоте в параллелепипед поместится 4 куба с гранью 1 см;
- по ширине – 3 штук;
- по длине – 5 кубиков.
Вторая формула необходима, когда входными данными является площадь одной из поверхностей (S) и длина третьей поверхности (h) или высота.Смысл расчета остается прежним — умножьте площадь поверхности на длину третьей стороны тела.
Косые параллелепипеды — это четырехгранные призмы с параллелограммом в основании, боковые грани которых образуют угол, отличный от 90°.
Объем наклонного параллелепипеда
Площадь и объем косого параллелепипеда вычисляются по той же формуле, что и для прямоугольника: V = S
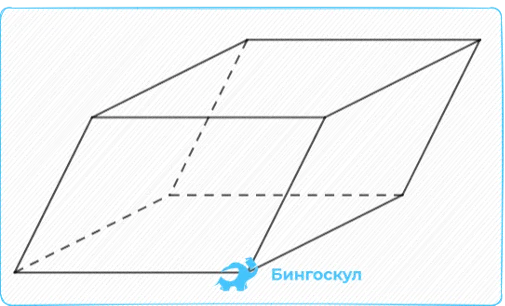
на базу) и длина третьей поверхности (h) или высота.Площадь рассчитывается по-разному, хотя
Определить объем параллелепипеда довольно просто. Для этого необходимо знать длину трех сторон или двух сторон и высоту. Чтобы облегчить вычисление объема параллелепипеда, мы разработали два калькулятора для разных исходных данных. Просто введите известные значения и получите результат в режиме онлайн.
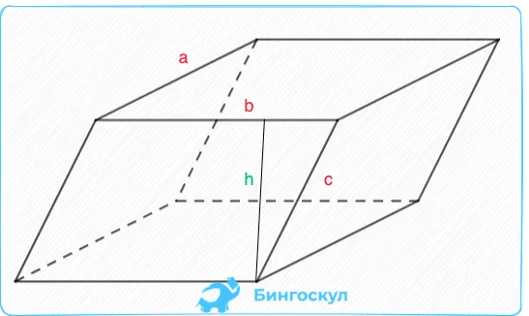
S = S1+ S2+S) и длина третьей поверхности (h) или высота.Параллелепипед — это кубоид, у которого все стороны прямоугольные.1Формула для определения объема параллелепипеда по его высоте и сторонам:2Где a, b — стороны параллелепипеда, а h — высота.) и длина третьей поверхности (h) или высота.Формулу можно использовать как для прямоугольника, так и для косого параллелепипеда.
Мы хотим определить объем кубоида с длинами сторон 3 см, 4 см и 5 см. Подставим эти значения в первую формулу и выполним вычисления:
Вы также можете найти объем конуса на нашем сайте.
Объем параллелепипеда
Вы также можете найти конус на конусе в конусе, используя тот же конус.
Итак, чтобы рассчитать формулу, вам нужно знать длину, ширину и высоту объекта, который вы хотите измерить. Эти данные следует обозначать соответственно буквами A, B и C, а объем обычно обозначается буквой V. Формула для определения объема кубоида в этом случае выглядит следующим образом.
Чтобы определить объем бассейна, необходимо перемножить его длину, ширину и глубину. Для лучшего понимания объясним правила вычисления объема кубоида на примере. Предположим, что его длина составляет 10 метров, ширина — 3 метра, а глубина — 1,5 метра. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5 = 45 кубических метров, или 45 кубических метров.
Объем параллелепипеда через стороны и высоту
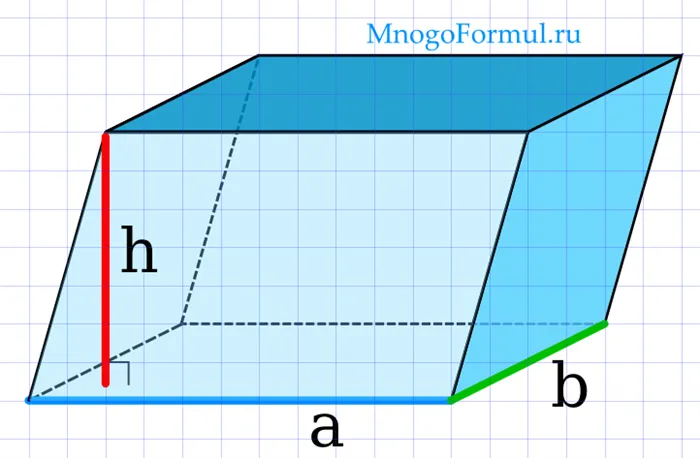
Можно вывести и другую формулу, которая имеет некоторое отличие. Это произведение площади основания и высоты. Формула выглядит следующим образом: V = S x h. Где h — высота параллелепипеда. S — площадь основания, которая является произведением двух сторон основания. Обычно обозначаются как a и b: S = a x b.
Чтобы вычислить объем параллелепипеда, нужно знать, что это за фигура. Это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, каждая из которых является параллелограммом. Существует несколько типов элементов. Принцип расчета не имеет особых отличий, но сами цифры отличаются по внешнему виду. Таким образом, можно выделить следующие типы:
Также важно помнить, что каждый компонент формулы при расчете должен иметь одинаковую размерность. Если вы не будете соблюдать это простое правило, вы получите правильное значение p
Пример расчета
Не стоит думать, что основные математические формулы для определения объема геометрических фигур можно найти только на уроках математики. В большинстве случаев они пригодятся в дальнейшей жизни. Особенно в ремонтных или строительных работах, в дизайне и оформлении интерьера и во многих других ситуациях. В этом случае правильная формула имеет решающее значение.
Подведем итог: объем кубоида равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при каждом вращении и обороте. Результат не изменится.
— Бим, давай отведем обезьян в цирк, — Боб посмотрел на часы, — им пора ужинать. Большое спасибо, ребята! Вы и Бим помогли нам понять, что такое объем, что такое кубоид, как определить объем кубоида и выучить единицы измерения объема. Увидимся в цирке!
Формула расчета в двух вариантах
Оригинальная идея подачи материала принадлежит Лилии Стуловой (учитель математики для детей в возрасте 5+).
Не забудьте похвалить наши усилия! Комментарии приветствуются. Следите за нами в Яндексе и других социальных сетях. )))
В электронный калькулятор можно вводить числа или дроби. Для получения дополнительной информации см. правила ввода цифр.
N.B. Эти значения можно использовать в онлайн-калькуляторе с теми же единицами измерения!
О чем еще следует знать для правильности расчета?
Если у вас возникают проблемы с преобразованием единиц, используйте конвертер единиц расстояния, единиц площади или единиц объема.
- Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
- Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
- Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.
Заключение
Найти объем прямоугольного параллелепипеда
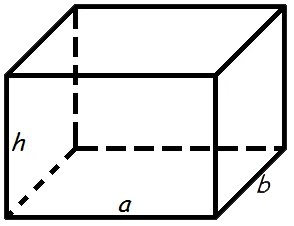Введите данные:
| a | = |
| b | = |
| h | = |
Ввод данных в калькулятор для вычисления объема прямоугольного параллелепипеда
Дополнительные возможности калькулятора для вычисления объема прямоугольного параллелепипеда
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
