Пунктирная линия состоит из нескольких сегментов, так называемых звеньев. Эти отрезки соединены своими концами и не образуют угол 180°.
Что такое отрезок
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, вводимых в начальной школе, является отрезок. Многие задачи по математике и геометрии основаны на понятии прямого отрезка и прямой линии.
Если вы понимаете, что такое отрезок прямой, вы сможете решать всевозможные задачи и примеры по математике, как в школе, так и во время учебы.
Отрезок — это геометрическая фигура
Согласно словарному определению, интервал — это отрезок прямой, ограниченный двумя точками. Называя эти точки, отрезок прямой становится отрезком прямой.
На диаграмме ниже показан отрезок AB. Точки A и B — это концы отрезка. Длина отрезка — это расстояние между его концами.

В математике мы используем латинские заглавные буквы для обозначения точек и, соответственно, отрезков. Если нужно нарисовать прямой отрезок, то его обычно показывают без прямой линии, а только от одного конца до другого.
Можно также сказать, что отрезок — это множество всех точек на прямой, которые лежат между двумя определенными точками, являющимися концами отрезка.
Если отметить еще одну точку на отрезке между его краями, то отрезок разделится на две части. Длина отрезка AB может быть рассчитана путем сложения длин отрезков AC и CB.
Разница между отрезком, лучом и прямой
Студенты иногда путают термины «прямая линия», «радиус» и «отрезок». Хотя эти понятия очень похожи, они в корне отличаются друг от друга:
- Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
- Луч — это часть прямой, ограниченная одной точкой. Он имеет начало и не имеет конца.
- Отрезок ограничивается двумя точками. Он имеет и начало, и конец.
Точка на прямой делит ее на два луча. Количество отрезков на одной прямой может быть бесконечным.
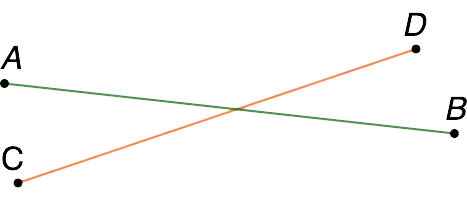
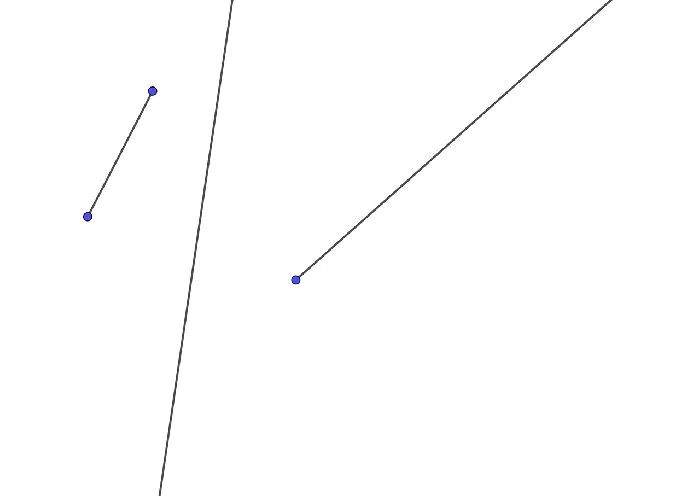
Чтобы выделить эти элементы на чертеже, точки ставятся в начале и в конце линии, которая должна быть нарисована или нет. Точка находится на одном конце луча, а точка — на обоих концах прямой. Линия не имеет концов, поэтому в конце линии не ставится точка.
Обозначение отрезков
Отрезок прямой определяется по его конечным точкам. Отрезок прямой на рисунке 1 называется AB или BA. Порядок названий конечных точек не важен.
Чтобы сравнить сегменты, вы должны:
- Взять любую прямую и отметить на ней какую-нибудь точку.
- Отложить на прямой оба отрезка из отмеченной точки на прямой на одну и ту же сторону.
Если два других конца находятся вместе, то отрезки одинаковы. Если конец одного отрезка находится внутри другого, то длина первого отрезка короче второго.
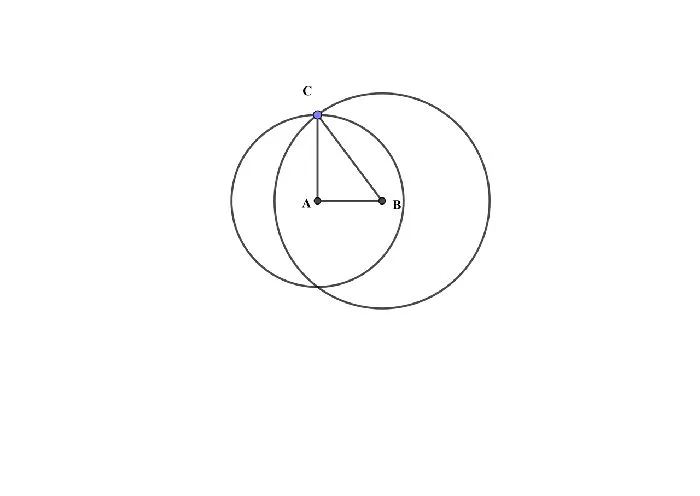
Сравните два отрезка AB и CD (рис. 2), т.е. определите, какой из них длиннее. Постройте эти отрезки на прямой a. Видно, что точка D лежит внутри прямой AB. Следовательно, отрезок CD короче AB. Это представлено компакт-диском. Чтобы определить длину отрезка, нужно сравнить его с другим отрезком как единицей измерения. Единицей измерения может быть, например, сантиметр. В данном случае, чтобы определить длину отрезка, нужно выяснить, сколько раз сантиметр помещается в этот отрезок. Это длина отрезка, выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то AB = 3 см. Если отрезок, взятый за единицу, не помещается целое число раз в измеряемый отрезок, его обычно делят на 10 равных частей и определяют, сколько раз такая часть помещается в остаток. Десятая часть процента называется тысячной долей. Результат — длина отрезка в сантиметрах и миллиметрах. На рисунке 4 1 сантиметр откладывается 4 раза в AB, а остаток откладывается ровно на 8 десятых сантиметра. Поэтому мы можем писать. Когда вы задаете направление для сегмента линии, он называется направленным сегментом линии. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуется стрелка (рис. 5). Напишите начальную, а затем конечную точку направленного отрезка. На рис. 2 верхний направленный сегмент обозначен следующим образом: \( \маленькая \направленная стрелка \) и нижний сегмент выглядит так: \( \маленькая \направленная стрелка \) Отрезок направления называется вектором. Построим треугольник со сторонами 3, 5 и 4. Каждая из сторон является отрезком определенного размера. Это еще одно свойство сегментов. Три отрезка определенного размера всегда можно использовать для построения треугольника. Сначала начертите отрезок AB=3. Вы можете выбрать любое другое значение из заданных. В данной конкретной задаче этот выбор чисел сделан для того, чтобы можно было провести дальнейшую проверку. Возьмите точку A за центр окружности радиусом 4 и начертите ее. Тогда точка B — центр окружности радиуса 5. На пересечении двух окружностей находится точка C — третья точка треугольника. Треугольник со сторонами 3, 4 и 5 — это классический правильный треугольник. То же самое относится к пробам 3, 4 и гипотенузе 5. Эти соотношения были выведены в Древней Греции и очень часто используются сегодня в простых задачах на решение прямоугольных треугольников. Конкретно в нашем случае это означает, что полученный треугольник должен быть ортогональным в соответствии с теоремой Пифагора. 25=25 верно, условие выполнено. И на рисунке видно, что треугольник построен правильно. При построении любого треугольника из трех заданных отрезков заранее убедитесь, что выполняются условия неравенства треугольника: одна сторона всегда меньше суммы двух других сторон. Постройте значения на арифметическом радиусе. Каждая фракция имеет свое собственное значение. $<5\over6>$ обозначается дробью OA. Она будет меньше, чем единичная дробь $<7\over15>Мы будем обозначать его через OB. Она также будет меньше единичной дроби $<18\over4>Мы обозначаем его сегментом OS. Оно будет больше, чем значение 4, нарисованное на числовой прямой. $<25\over7>Обозначим $ сегментом OD, который будет находиться между 3 и 4. Поэтому вместо того, чтобы сравнивать 4 дроби, нам нужно сравнить только две: $<5\over6>$ и $<7\over15>$. Разложим 6 и 15 на простые числа и найдем НОК. Итак: $<5\over6>><7\over15>$ — теперь мы можем указать точное местоположение этих номеров. Сравнение проведено, проблема решена. Пунктирная линия — это серия соединенных отрезков, где конец одного отрезка совпадает с началом другого. Каждый из элементов пунктирной линии называется ссылкой. Пунктирная линия имеет три типа вершин — точек, из которых состоят отрезки: Первая и последняя ссылкаДлина отрезка
Направленный отрезок
Содержание раздела
Задача на построение
Задача с числовым лучом
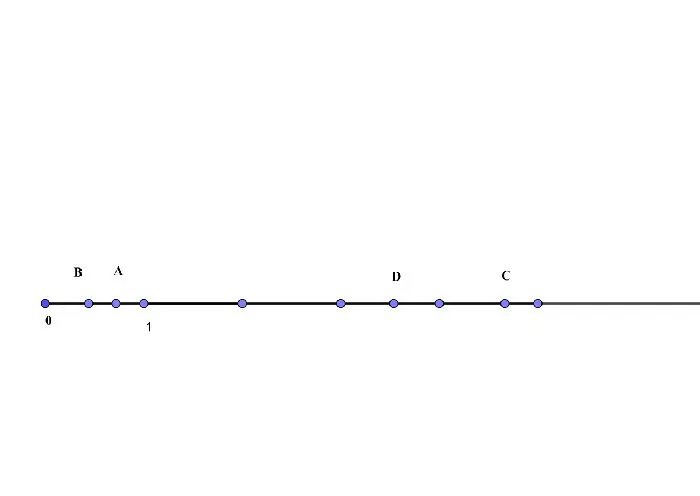
Отрезки, соединённые в ломаную линию
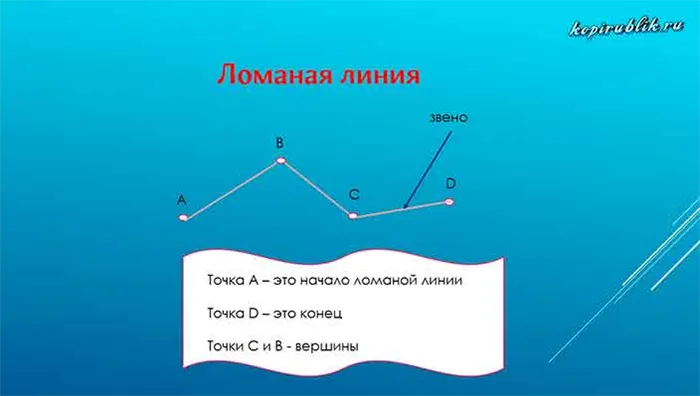
Сравнение отрезков

Отрезок: разные значения слова








